Alkutoimia

# testaukseen 7.11.2020 virheilmoituksia varten arvo TRUE
options(tinytex.verbose = TRUE)

29.11.2020 Oikoluettu valmis versio - versio 2.1 viimeiset korjaukset

Tämä luku poistetaan kun tutkielma on valmis

Raportti yhtenä html-tiedostona (https://hirjus.github.io/capaper/JH_capaper.html)

PDF-tulostus oikuttelee ja kaatuu, mutta pdf-syntyy. MikTeX vaihdettu TinyTeX-engineen ja pdflatex -> xelatex (15.11.20). PDF-tulostus kaatuu luultavasti koodilistaukseen. Pandoc ei osaa rivittää koodia oikein tms. Koodilistauksen poistaminen ei auta, syystä tai toisesta.

Suunnitelma: PDF html-raportista -> pdfExchange-ohjelmalla sivunumerot ja kansilehdet

RefWorksistä tuotu jhca2020.bib-tiedosto tarkistettu ja korjailtu virheet. Ei enään ladata uutta (21.11.2020), packages.bib (r-pakettien viitekanta) tarkistettu ja korjattu erikoismerkit. Ei päivitetä enään (24.11.20)

Data-analyysi: (https://hirjus.github.io/Galku).

Luku 1 Johdanto

Korrespondenssianalyysi on deskriptiivinen data-analyysin menetelmä, joka soveltuu erityisesti luokitteluasteikon muuttujien yhteyksien analyysiin. Yksinkertainen esimerkki on kahden luokittelumuuttujan taulukko. Yksinkertainen korrespondenssianalyysi esittää taulukon rivien ja sarakkeiden riippuvuuden graafisesti, kaksiulotteisena karttana. Kahden muuttujan analyysin perusideat soveltuvat myös useamman muuttujan yhteyksien kuvaamiseen.

Taulukoita on kaikkialla, mutta niiden graafinen analyysi ei ole kovin yleistä.

1.1 Tutkielman tavoite ja toteutus

Tämän tutkielman tavoite on esittää korrespondenssianalyysin periaatteet data-analyysin sovellusten avulla. Tutustuin aiheeseen Michael Greenacren luennoilla Helsingissä keväällä 2017. Aivan huomaamatta tein harjoitustehtävinä karttoja, joita en oikein ymmärtänyt.

Pyrin esittelemään menetelmän niin, että data-analyysistä kiinnostunut lukija oivaltaa karttojen tulkinnan perusperiaatteet. Tilastotieteessä on aina ollut osana käytännöllinen, soveltajille suunnattu menetelmien esittely. En kirjoita kuitenkaan oppikirjaa, vaan tutkielman, jossa esittelen aineiston analyysin avulla menetelmää. Analyysien r-koodi on vapaasti saatavilla verkossa, kuten tämän tutkielman käsikirjoitus.

En etsi datasta vastauksia joihinkin substanssikysymyksiin vaan havainnollistan menetelmän mahdollisuuksia datan analyysissä. Tavoitteena on myös oman ymmärryksen lisääminen.

Tutkielman toteutus on rakennettu kolmelle perusajatukselle.

Yksinkertainen kahden luokittelumuuttujan korrespondenssianalyysi antaa graafisen analyysin ”…perussäännöt tulkinnalle. Kaikki muut korrespondenssianalyysin muodot ovat saman algoritmin soveltamista toisen tyyppisiin datamatriiseihin, ja tulkintaa sovelletaan vastaavasti (with the consequent adaptation of the interpretation)”(Greenacre ja Hastie (1987) s. 437). Tutkielman laajin osa on yksinkertaisen korrespondenssianalyysin tulosten ja peruskäsitteiden esittelyä.

Toiseksi käytän laajaa ja laadukasta kansainvälisen haastattelututkimuksen aineistoa. Korrespondenssianalyysi sopii survey-aineistojen analyysiin mainiosti, ja samaa dataa on käytetty alan oppikirjoissa ja artikkeleissa esimerkkiaineistona. Laaja ja mutkikas aineisto antaa oikean kuvan data-analyysistä ja samalla ohjaa analyysin kulkua. Data yllättää aina. Menetelmän on taivuttava tarvittaessa uusiin suuntiin. Tutkielman data-analyysissä jouduin moneen kertaan miettimään mihin suuntaan kannattaisi edetä. Datan analyysi tuo esiin sen ominaisuuksia, vaikka mitään sisällöllistä tutkimusongelmaa ei ole määritelty.

Kolmanneksi keskityn graafiseen analyysiin, kuvien tulkintaan. Korrespondenssianalyysin idea on esittää mutkikkaat riippuvuudet ja yhteydet kuvana. Samalla tavoite on tiivistää moniulotteisen datan informaatiosta mahdollisimman paljon kaksiulotteiselle kartalle. Informaatiota menetetään, ja tulkinnan varmistaminen numeerisista tuloksista estää virhepäätelmät. Kartan lukeminen ei ole aivan helppoa, mutta perussäännöt ovat melko selkeät. Graafinen data-analyysi on tasapainoilua datan analyysin ja tulosten esittämisen välillä. Tässä painottuu data-analyysi, ei vaativa viimeisteltyjen graafisten esitysten suunnittelu ja toteutus. Graafinen data-analyysi ei aina ole helppoa ja nopeaa.

1.2 Korrespondenssianalyysin historiaa

Korrespondenssianalyysi on 80-luvun alusta vähitellen vakiinnuttanut asemansa yhtenä ei-parametrisen kuvailevan data-analyysin menetelmänä. Kansainvälinen tutkijaverkosto CARME (Correspondence analysis and related methods network) järjesti ensimmäisen konferenssin 1991 (http://www.carme-n.org).

Korrespondenssianalyysi esitellään oppikirjoissa muiden menetelmien rinnalla. Hyviä esimerkkejä ovat ekologisen datan monimuuttujamenetelmien (M. Greenacre ja Primicerio 2013), kaksoiskuvien (Greenacre 2010) ja “koostumusdatan” (compositional data) (Greenacre 2018) kirjat. Suomessa korrespondenssianalyysi esitellään ainakin kahdessa oppikirjassa (Mustonen (1995) , Vehkalahti (2008)).

Korrespondenssianalyysi ja koulukunta syntyi ja vakiintui Ranskassa Jean - Paul Benzecrin (1932-2019) ympärille 60-luvulla. Ranskassa 70-luku oli “Analyse des Donnees” -liikkeen kultainen kausi. Kansaivälisesti se oli kuitenkin “loistavan eristyksen” aikaa. Vasta 80-luvulla menetelmä ylitti kielimuurin, ehkä osittain menetelmää soveltaneen sosiologi Pierre Bourdieun kansainvälisesti tunnettujen tutkimusten ansiosta. Benzecrin oppilaista Greenacre on oppikirjoillaan vaikuttanut paljon menetelmän vakiinnuttamiseen osaksi tilastotieteen perustekniikoita. Näiden kirjojen kansissa ei turhaan lue “…in practice”.

Toisena muurina on pidetty ranskalaisen koulukunnan tiukkaa “bourbakilaista” matemaattista esitystapaa. LeRoux ja Rouanet (2004) esittelevät tämän lähestymistavan englanniksi. Lyhyt historiallinen katsaus ja menetelmä soveltamisen perusajatusten esittely valaisevat ranskaa taitamattomalle data-analyysin koulukunnan ideoita. Kirjassa esitellään myös perusteellisesti muutama empiirinen tutkimus.

Eristys on päättynyt, ja tarina on kiinnostava osa tieteenhistoriaa.

1.3 Tutkielman rakenne

Datan esittelyn jälkeen esitellään korrespondenssianalyysin peruskäsitteet yksikertaisen esimerkin avulla luvussa 3.

Luvuissa 4 - 5 analyysiin lisätään täydentäviä pisteitä tulkinnan tueksi ja muodostetaan luokittelumuuttujien yhteisvaikutusmuuttujia (ikä ja sukupuoli).

Kolmen yhteisvaikutusmuuttujan (maa, sukupuoli ja ikäluokka) analyysi tehdään osajoukon korrespondenssianalyysillä luvussa 6.

Luvussa 7 esitellään lyhyesti kaksi tapaa tutkia useamman muuttujan yhteyksiä. Taulukoita yhdistämällä voidaan analysoida kahden muuttujaryhmän välisiä yhteyksiä. Monimuuttujakorrespondenssianalyysia (MCA) sovelletaan isoon aineistoon ja tällaisten aineistojen yleiseen ongelmaan, puuttuviin tietoihin. Menetelmällä tutkitaan yhden muuttujajoukon sisäisiä yhteyksiä.

Luvussa 8 sisältää yhteenvedon. Varsinaisten kahdeksan luvun lisäksi tutkielmassa on kolme liitettä.

Liite 1 esittelee tiiviisti menetelmän teorian. Korrespondenssianalyysin numeerisia tuloksia havainnollistetaan kuvalla, ja monimuuttujakorrespondenssianalyysin (MCA) käsitteitä esitellään hieman enemmän. MCA:n teoriaa ei käsitellä laajemmin, mutta tulkinnan ongelmat esitellään lyhyesti.

Tutkielma on tehty R-tilasto-ohjelmalla, ja korrespondenssianalyyseissä on käytetty ca-pakettia( Nenadic ja Greenacre (2007) ).

Tutkielman koodi on julkaistu Github-palvelussa (https://github.com/hirjus/capaper), samoin tutkielman käsikirjoitus (https://hirjus.github.io/capaper/ ) ja alustava data-analyysi.

Tekninen ympäristö on kuvattu tarkemmin liitteessä 2, myös sen ongelmat.

Liitteessä 3 on listattu tutkielman R-koodi.

1.4 Tärkeimmät lähteet

Tutkielman tärkein lähde on (M. J. Greenacre 2017) (jatkossa CAiP), ja muitakin saman tekijän artikkeleita on käytetty paljon. Kevään 2017 kurssimateriaali (M. Greenacre 2017) ja laskuharjoitusten koodi on ollut hyödyllinen pikaopas peruskäsitteisiin ja r-toteutuksen ratkaisuihin.

Carme-verkoston kolmas artikkelikokoelma (M. Greenacre ja Blasius 2006) on ajantasainen perusteos. Perusteelliset artikkelit kattavat myös korrespondenssianalyysin tärkeimmät aiheet.

Data on ensin luettava ohjelman ymmärtämään muotoon, ja erilaiset muunnokset kannattaa tehdä heti kun data luetaan. McNamara ja Horton (2018) kertovat, miten luokittelumuuttujia pitää R-koodissa käsitellä.

Luku 2 Data

Käytän tutkielmassa International Social Survey - projektin (ISSP) vuoden 2012 kyselytutkimusta “Perhe, työ ja sukupuoliroolit” (International Social Survey Programme: Family and Changing Gender Roles IV). Tutkimuksen aikaisempien toteutusten dataa on käytetty tutkielman tärkeimmissä lähteissä esimerkkidatana.

Länsi-Saksan ja USA:n tutkimuslaitosten yhteistyö vakiintui ISSP-organisaatioksi 1984 (http://www.issp.org). Vuonna 2015 neljän perustajajäsenen joukko oli kasvanut 49 maahan. Vertailevan tutkimuksen aineistoja on kerätty monista teemoista, perhearvoista ja naisten työmarkkina-asemasta neljä kertaa (1988, 1994, 2002, 2012). USA:n edustajana mukana ollut Tom W. Smith näkee aineistojen arvon juuri kansainvälisessä vertailevassa tutkimuksessa. Järjestön julkaisuluettelossa oli 2012 yli 5200 julkaisua. Viime vuosina luetteloon on lisätty noin 400 julkaisua vuodessa (Smith 2015).

Data ja dokumentaatio on vapaasti saatavilla saksalaisen GESIS-tutkimuslaitoksen ylläpitämästä data-arkistosta (https://www.gesis.org/en/issp/home). Suomessa tutkimuksen data ja dokumentaatio löytyvät Tampereen yliopiston Aila-tietoarkistosta (https://services.fsd.uta.fi/catalogue/FSD2820?tab=summary&study_language=fi).

GESIS-instituutin ”datakatalogista”(https://zacat.gesis.org) löytää kätevästi kaiken dokumentaation ja datan (ISSP 2016), mutta edes saksalaiset eivät voi estää www-sivustojen innokkaita uudistajia. Monet linkit lähdeluettelossa vievät GESIS-arkistosivulle, josta löytyy pitkä lista pdf-dokumentteja.

Taulukkoon 2.1 on koottu neljän tärkeimmän dokumentin tiedostonimet ja lyhyt kuvaus.

Taulukko 2.1: ISSP 2012: tärkeimmät dokumentit
dokumentti	sisältö	tiedosto
Variable Report	Perusdokumentti, muuttujien kuvaukset ja taulukot	ZA5900_cdb.pdf
Study Monitoring Report	tiedokeruun toteutus eri maissa	ZA5900_mr.pdf
Basic Questionnaire	Maittain sovellettava kyselylomake	ZA5900_bq.pdf
Contents of ISSP 2012 module	substanssikysymykset taulukkona	ZA5900_overview.pdf
Questionnaire Development	kyselylomakkeen laatiminen	ssoar-2014-scholz_et_al-ISSP_2012_Family_and_Changing.pdf

Tätä kirjoittaessa (10.11.2020) ISSP 2012 - aineisto löytyy osoitteesta [https://zacat.gesis.org/webview/index.jsp?object=http://zacat.gesis.org/obj/fStudy/ZA5900].

Koodikirja (“Variable report”) (GESIS 2016) selostaa tarkasti tietosisällön. Tutkimuksen seurantaraportti (“Study Monitoring Report”) (Gendall ja Randow 2016) kertoo miten tutkimus käytännössä toteutettiin. Kyselylomake (”ISSP 2012 - Family and Changing Gender Roles IV Basic Questionnaire” 2011), suomenkielinen versio (Tilastokeskus 2012) ja muut kieliversiot voivat olla hyödyllisiä. Tiedonkeruun tarkoitus ja kyselyn suunnittelun ideat kerrotaan omassa raportissa (Scholz ym. 2014).

2.1 Aineiston rajaaminen

Olen rajannut laajasta aineistosta 25 maata ja joukon muuttujia. Maat on valittu niin, että ne ovat suhteellisen samankaltaisia ja valitut muuttujat ovat niissä samanlaisia. Kysymyksissä on jonkin verran pieniä eroja, mutta joissain tapauksissa ero on merkittävä. Esimerkiksi Espanja on jostain syystä jättänyt tässä käytetyistä muuttujista ns. neutraalin (”en samaa enkä eri mieltä”) vastausvaihtoehdon pois, joten jätin Espanjan pois tutkielmani analyyseistä.

Substanssimuuttujat ovat yksi ”kysymyspatteri”, jolla luodataan asenteita naisten roolista työmarkkinoilla. Aiheen pysyvää ajankohtaisuutta kuvaa hyvin The Economist - lehden artikkeli Saksojen jälleenyhdistymisen 30-vuotispäivänä (3.10.2020, “A report…reveals the interplay between policy and attitudes that influences the decision to work.”). Artikkeli on maksumuurin takana mutta tutkimus on vapaasti luettavissa (DIW Weekly Report 38 / 2020, S. 403-410)

Taulukon 2.2 kysymysten lyhyet versiot ovat datassa mukana. Sarakkeessa “muuttuja” on alkuperäisen aineiston muuttujanimi, kysymyksen tunnus on valittuun dataan luotu muuttujanimi.

Taulukko 2.2: ISSP2012:Työelämä ja perhearvot - kysymykset
muuttuja	kysymyksen tunnus, lyhennetty kysymys
V5	Q1a Working mother can have warm relation with child
V6	Q1b Pre-school child suffers through working mother
V7	Q1c Family life suffers through working mother
V8	Q1d Women’s preference: home and children
V9	Q1e Being housewife is satisfying
V10	Q2a Both should contribute to household income
V11	Q2b Men’s job is earn money, women’s job household
V12	Q3a Should women work: Child under school age
V13	Q3b Should women work: Youngest kid at school
SEX	Respondents age
AGE	Respondents gender
DEGREE	Highest completed degree of education: Categories for international comparison
MAINSTAT	Main status: work, unemployed, in education…
TOPBOT	Top-Bottom self-placement (10 pt scale)
HHCHILDR	How many children in household: children between [school age] and 17 years of age
MARITAL	Legal partnership status: married, civil partership…
URBRURAL	Place of living: urban - rural

Kyselylomakkeilla kysymykset olivat hieman pidempiä. Kuva 2.1 on osa suomenkielistä lomaketta.

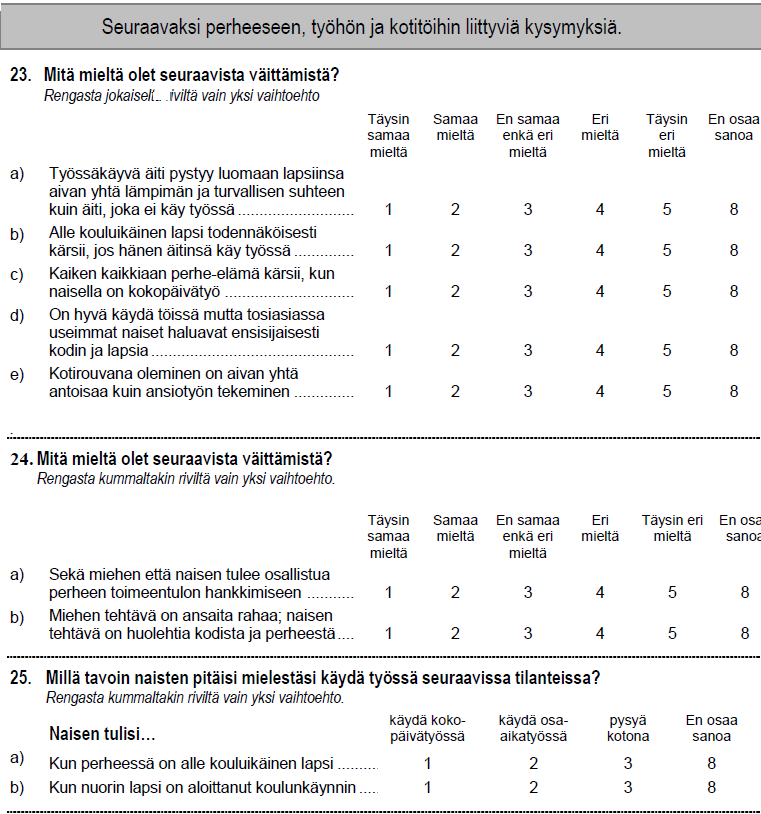
Kuva 2.1: Suomenkielinen lomake

Valituista taustamuuttujista monet on kerätty haastattelulla. Tiedonkeruu, otantamenetelmät ja yksikkövastauskadon (unit non-response, otokseen valitulta ei saada mitään tietoja) huomioiminen on tehty joka maassa omalla tavallaan. Aineistoissa on mukana painot, joilla tulokset voidaan korottaa perusjoukon tasolle, mutta kansainvälisiä vertailupainoja ei syystä tai toisesta ole. Taustamuuttujat kuten koulutustaso on harmonisoitu vertailukelpoisiksi.

Tutkimuksen kohdeperusjoukko on 18-vuotiaat tai sitä vanhemmat, poikkeuksina Suomi (15 - 74 vuotiaat), Islanti, Japani, Etelä-Afrikka ja Venezuela.

Jos ohitetaan pienet erot kysymyksissä ja vastausvaihtoehdoissa jäljelle jää erävastauskato. Erävastauskadolla tarkoitetann tilannetta, jossa joihinkin kysymyksiin ei vastata. Esimerkiksi Ranskassa yli 20 prosenttia kieltäytyi vastaamasta lasten lukumäärää kysyttäessä (HHCHILDR), ja aika moni kieltäytyi vastaamasta myös muihin perherakenteeseen liittyviin kysymyksiin. Tässä tutkielmassa monimuuttujakorrespondenssianalyysiä käytetään puuttuneisuuden analyysiin.

Poistin aineistosta havainnot, joissa tieto iästä tai sukupuolesta puuttuu (32969-32823 = 146 havaintoa).

Aineiston luokittelu- ja järjestysasteikon muuttujat muunnetaan R-ohjelmiston factor-tietotyypiksi. Teen muunnokset useammassa vaiheessa heti kun data on luettu SPSS-tiedosta. Käsittelyssä pyrin noudattamaan helposti toistettavan tutkimuksen periaatteita (McNamara ja Horton 2018). Koodi ei saisi olla kovin virhealtista (”haurasta”) ja tarkistuksia tehdään paljon. Data-analyysin ja ehkä erityisesti korrespondenssianalyysin idea on kuitenkin operoida matriiseilla, lisätä ja poistaa rivejä ja sarakkeita ja rakennella mutkikkaampia matriiseja yksinkertaisemmista. Analyysivaiheessa koodi muuttuu hauraammaksi.

Aineisto ja korrespondenssianalyysi

Michael Greenacre on käyttänyt aineistoa eri vuosilta luentomateriaaleissa kuten Helsingissä 2017 (M. Greenacre 2017) ja ainakin kahdessa oppikirjassaan ((Greenacre 2010), (M. J. Greenacre 2017)). ISSP - aineistoa vuodelta 1989 on käytetty myös neljän singulaariarvohajoitelmaan perustuvan menetelmän vertailuun (Greenacre 2003). Blasius ja Thiessen (Blasius ja Thiessen 2006) arvioivat aineiston laatua ja maiden vertailtavuutta vuoden 1994 aineistolla.

Sukupuoliroolien (gender roles) ja niihin liittyvien asenteiden vertailevaa kansainvälistä (cross-cultural) tutkimusta on tehty paljon. Tutkimusongelman sisällöllisten ja teoreettisen kysymysten nykytilaa kuvaa tuore artikkeli (Walter 2018).

Ferragina ja Seeleib-Kaiser (2015) tutkivat ensin 18 OECD-maan perhepolitiikan muutoksia kolmen viime vuosikymmenen ajalta. Näkökulma on työllisyyspolitiikka ja menetelmänä monimuuttuja-korrespondenssianalyysi (MCA). Havaituille kehityssuunnille etsitään toisessa vaiheessa selityksiä. Aineistona on viisi kansainväliseen vertailuun soveltuvaa aineistoa, yhtenä niistä ISSP:n data kolmelta kierrokselta (1988,1994,2002).

Luku 3 Yksinkertainen korrespondenssianalyysi

Korrespondenssianalyysin peruskäsitteet ja muuttujien yhteyden graafisen analyysin periaatteet voi esittää kahden luokittelumuuttujan ristiintaulukoinnin eli kontingenssitaulun analyysin avulla. Kyse ei ole pelkästään helposta esimerkistä, vaan peruskäsitteet ja geometrisiin perusteisiin nojaava graafinen analyysi ovat oleellisilta osin samat myös monimutkaisemmissa menetelmän sovelluksissa (Greenacre ja Hastie 1987).

Greenacren oppikirjat ovat hyvä esimerkki perusteellisesta yksinkertaisen taulukon analyysin esitystavasta. LeRoux ja Rouanet (2004) korostavat ranskalaisen perinteen mukaisesti matemaattista teoriaperustaa, mutta menetelmän peruskäsitteet ja tulkinnat esitellään yksinkertaisella esimerkillä. Mustonen (1995) käyttää samaa Fisherin Cairness-aineistoa korrespondenssianalyysin esittelyyn.

Esitän tässä luvussa korrespondenssianalyysin peruskäsitteet intuitiivisesti, matemaattiset yksityiskohdat löytyvät liitteestä 1. Kun taulukko on pieni, johtopäätökset voi helposti tarkastaa datasta. Datan analyysin tärkein väline on kuva, yleensä kaksiulotteinen kartta. Tulkinta ja erityisesti väärien johtopäätösten välttäminen vaati kartan tulkinnan varmistamista ratkaisun numeerisista tuloksista. Analysoitava taulukko, sen rivien ja sarakkeiden riippuvuuksia kuvaava kartta ja kartan perustana olevat numeeriset tulokset esitetään yhdessä. Näin tulkinnan perussäännöt on helpompi ymmärtää.

LeRoux ja Rouanet (2004) esittävät tulkinnan perussäännöt hieman eri korostuksella kuin Greenacre (CAiP). Yhteistä on graafisen analyysin tärkeys, mutta ranskalaiset tutkijat korostavat numeeristen tulosten ensisijaisuuta. Analyysi pitää aloittaa tutkimalla numeerisen ratkaisun ominaisuuksia. Greenacren mielestä numeerisia tuloksia tarvitaan johtopäätösten varmistamiseen, ensin katsotaan karttaa. Eroa ei kannata liioitella, molempia tarvitaan. Eksploratiivisessa data-analyysissä näkökulmaa muutetaan, kun datan ominaisuudet tai omituisuudet havaitaan. Kun kartat ovat aina approksimaatiota, numeerisia tuloksia tarvitaan.

3.1 Äiti töissä - kärsiikö lapsi?

Aineistossa on kuuden maan vastaukset kysymykseen Q1b: ”Alle kouluikäinen lapsi todennäköisesti kärsii, jos hänen äitinsä käy työssä”. Kysymys on voimakkaasti muotoiltu. Eräs lastensuojelun ammattilainen piti vastaamista mahdottomana, pitäisi tietää missä lapsi on ja mitä hän tekee. Kysymykset on kuitenkin suunniteltu kokonaisuudeksi, ja niitä analysoidaan yhdessä luvussa 7. Yhden taulukon analyysi esittelee menetelmän, oikeassa tutkimuksessa pitää käyttää vähintään koko kysymyssarjaa.

Tässä tutkielmassa käytetystä aineistosta on poistettu havainnot, joissa tieto vastauksesta puuttuu. Taustamuuttujia ovat vastaajan sukupuoli ja ikä. Taulukoissa vastausvaihtoehtojen tunnuksina käytetään samoja symboleja kuin kuvissa (E = täysin eri mieltä, e = eri mieltä, ? = ei samaa eikä eri mieltä, s = samaa mieltä, S = täysin samaa mieltä).

Frekvenssitaulukossa 3.1 on esitetty vastausten suhteellinen jakauma, lukumäärät on jaettu havaintojen lukumäärällä (8143). Korrespondenssianalyysissä kaikki on suhteellista, ja analyysi perustuu tähän taulukkoon. Taulukon reunajakaumat kertovat jokaisen maan ja jokaisen vastausvaihtoehdon suhteellisen osuuden. Näitä suhteellisia osuuksia kutsustaan korrespondenssianalyysissä rivi- ja sarakemassoiksi.

Taulukko 3.1: Kysymyksen Q1b vastaukset, suhteelliset frekvenssit
	S	s	?	e	E	Total
BE	2.35	5.54	5.38	6.78	4.68	24.72
BG	1.45	4.85	2.52	2.33	0.16	11.31
DE	2.03	4.61	2.43	6.61	5.38	21.05
DK	0.86	2.92	1.87	2.85	8.55	17.05
FI	0.58	2.31	1.83	5.19	3.72	13.63
HU	2.69	3.54	2.76	2.33	0.92	12.24
Total	9.95	23.76	16.79	26.10	23.41	100.00

Muuttujien luonne on usein erilainen. Tähän aineistoon sopii riviprosenttientaulukko, vertaillaan vastausten jakaumia maiden välillä. Taulukon sarakkeet ovat muuttujia ja rivit havaintoja. Rivit on saatu summaamalla (aggregoimalla) vastaukset maittain. Greenacre käyttää näistä yksittäisten vastausten (havaintojen) summariveistä termiä “sample”.

Taulukko 3.2: Kysymyksen Q1b vastaukset, riviprosentit
	S	s	?	e	E	Total
BE	9.49	22.40	21.76	27.42	18.93	100.00
BG	12.81	42.89	22.26	20.63	1.41	100.00
DE	9.63	21.88	11.55	31.39	25.55	100.00
DK	5.04	17.15	10.95	16.71	50.14	100.00
FI	4.23	16.94	13.42	38.11	27.30	100.00
HU	21.97	28.89	22.57	19.06	7.52	100.00
All	9.95	23.76	16.79	26.10	23.41	100.00

Sarakeprosentit antavat toisen näkökulmaan samaan dataan.

Taulukko 3.3: Kysymyksen Q1b vastaukset, sarakeprosentit
	S	s	?	e	E	All
BE	23.58	23.31	32.04	25.98	19.99	24.72
BG	14.57	20.41	15.00	8.94	0.68	11.31
DE	20.37	19.38	14.48	25.32	22.98	21.05
DK	8.64	12.30	11.12	10.92	36.52	17.05
FI	5.80	9.72	10.90	19.91	15.90	13.63
HU	27.04	14.88	16.46	8.94	3.93	12.24
Total	100.00	100.00	100.00	100.00	100.00	100.00

Tavoitteena on korrespondenssianalyysin kartta, jossa rivi- ja sarakepisteet on esitetty samassa kuvassa. Sarakeprosenttien taulukossa on esitetty sarakkeiden suhteelliset jakaumat. Näitä suhteellisia rivejä ja sarakkeita kutsutaan korrespondenssianalyysissä rivi- ja sarakeprofiileiksi.

Korrespondenssianalyysin perusidea on analysoida rivien ja sarakkeiden yhteyttä (korrespondenssia) rivi- tai sarakeprofiilien hajonnan avulla. Hajontaa mitataan poikkeamilla keskiarvorivistä tai sarakkeesta, ja massat otetaan huomioon, kun poikkeamat lasketaan yhteen.

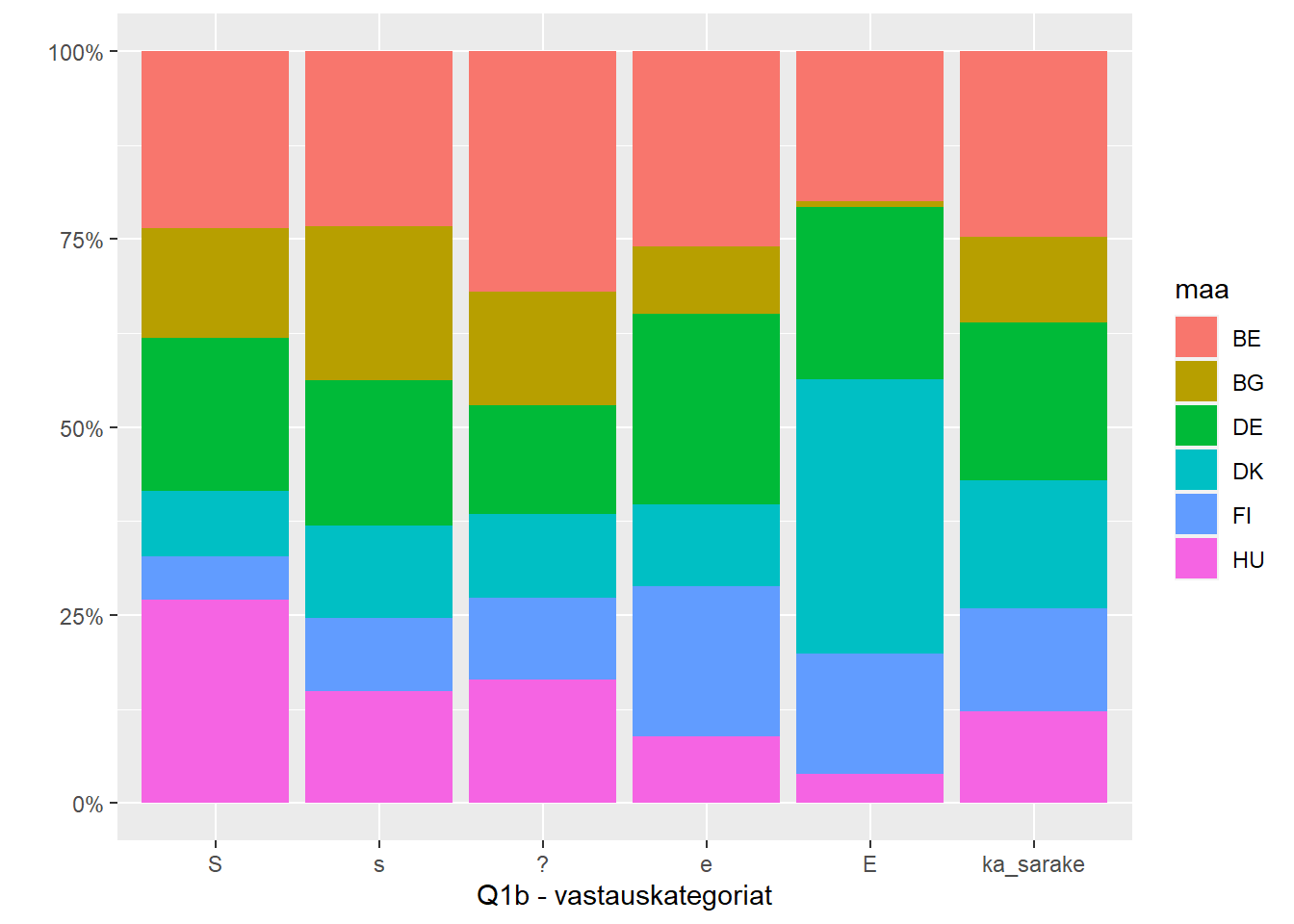
Kuva 3.1: Q1b:Sarakeprofiilit ja keskiarvoprofiili

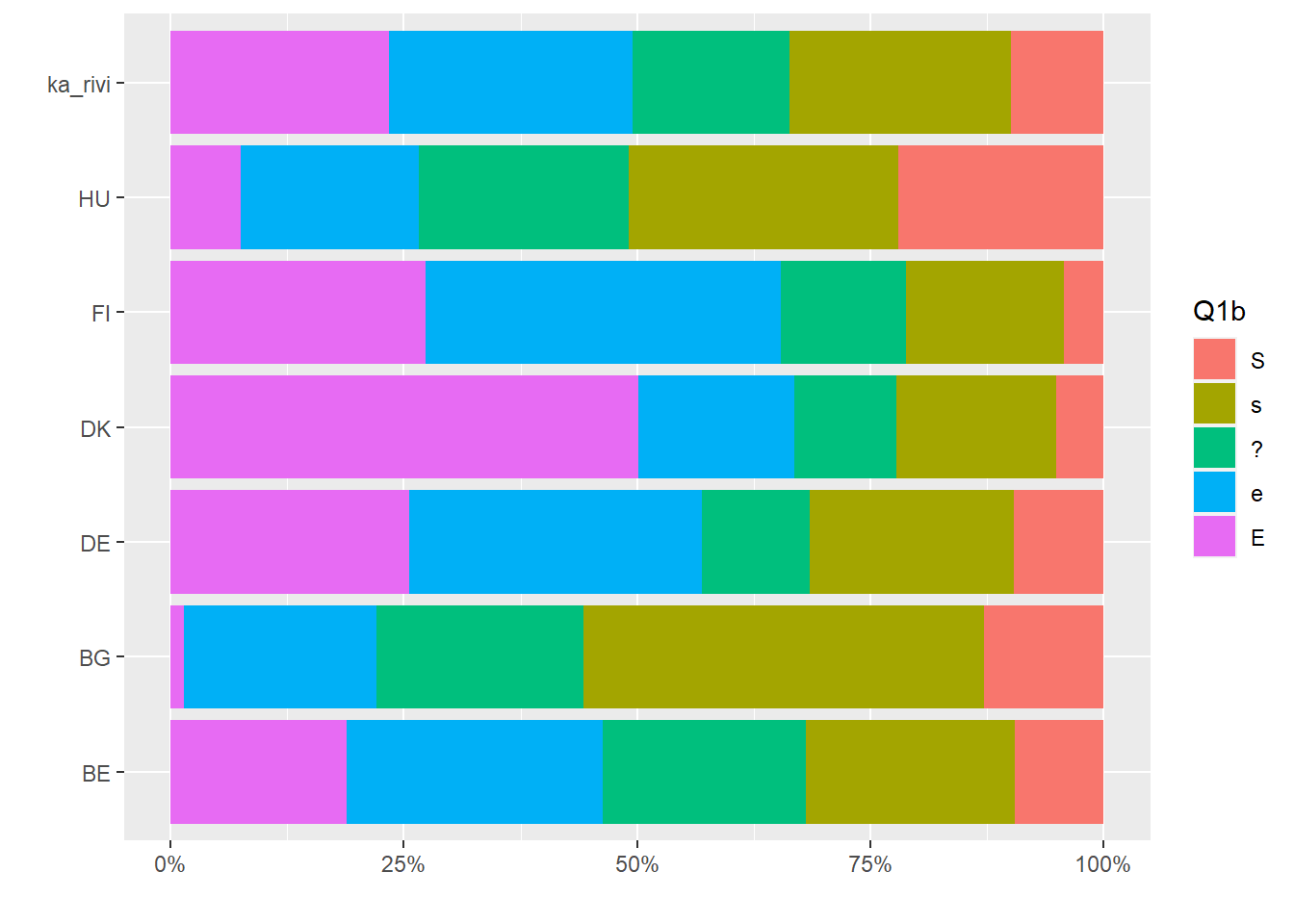
Kuva 3.2: Q1b: riviprofiilit ja keskiarvorivi

Kuvasta 3.2 esimerkiksi näkee, että Tanska (DK) näyttäisi poikkeava keskiarvorivistä paljon, samoin Bulgaria. Bulgarian massa on kuitenkin aineiston pienin (11,31 %), Tanskan taas kohtalainen (17 %). Sarakeprofiilikuvassa 3.1 täysin eri mieltä - vastaus (E) on selvästi erilainen ja sen massa on suuri (23 %). Kaikki luvut ovat suhteellisia, havaintojen lukumäärä ei vaikuta tulkintaan periaatteessa mitenkään.

Mikä on rivien ja sarakkeiden yhteys?

Kahden luokittelumuuttujan riippuvuutta voidaan testata \(\chi^{2}\) - testillä. Riippumattomuushypoteesin mukainen odotettu solufrekvenssi on taulukon 3.1 reunajakaumien alkioiden tulo.

Testisuure saadaan laskemalla yhteen jokaisen solun havaittujen ja odotettujen frekvenssien erotukset muodossa

\[\begin{equation} \chi^{2} = \frac{(havaittu - odotettu)^2} {odotettu}. \tag{3.1} \end{equation}\]

Tämä voidaan esittää korrespondenssianalyysin esittelyyn sopivammalla tavalla parilla muunnoksella, jolloin saamme riveittäin vastaavat termit rivisummalla painotettuna.

\[\begin{equation} rivisumma \times \frac{(havaittu \: riviprofiili - odotettu \: riviprofiili)^2} {odotettu \: riviprofiili}. \tag{3.2} \end{equation}\]

Kun jaamme nämä tekijät havaintojen kokonaismäärällä \(n\), rivisumma muuntuu rivin massaksi, ja niiden summa muotoon \(\frac{\chi^{2}}{n}\).

\[\begin{equation} \frac{\chi^{2}}{n} = \phi^{2}. \tag{3.3} \end{equation}\]

Jakajassa ei ole vapausastekorjausta (n-1), korrespondenssianalyysi on deskriptiivistä data-analyysiä.

Tunnusluku \(\phi^{2}\) on korrespondenssianalyysissä kokonaisinertia (total inertia). Se kuvaa, kuinka paljon varianssia taulukossa on ja inertia on riippumaton havaintojen lukumäärästä. Tilastotieteessä tunnusluvulla on useita vaihtoehtoisia nimiä (esim. mean square contingency coefficient) ja sen neliöjuurta kutsutaan \(\phi\) - kertoimeksi.

Korrespondenssianalyysin ratkaisussa käytetään suhteellisten frekvenssien taulukkoa.

Frekvenssitaulukossa kahden rivin (esimerkiksi rivien 1 ja 3) euklidinen etäisyys on

\[\begin{equation} \sqrt{(p_{11} - p_{31})^2 + (p_{12} - p_{32})^2 + (p_{13} - _{33})^2+ (p_{14} - _{34})^2+ (p_{15} - _{35})^2}. \tag{3.4} \end{equation}\]

Rivien \(\chi^{2}\) - etäisyys on painotettu euklidinen etäisyys, jossa painoina ovat riviprofiilin odotetut arvot. Ne ovat riippumattomuushypoteesin mukaisesti riviprofiilien keskiarvoprofiilin vastaavat alkiot \(r_{i}\) .

\[\begin{equation} \sqrt{\frac{(p_{11} - p_{31})^2} { r_{1}} + \dots + \frac{(p_{15} - p_{35})^2} {r_{5}}} \tag{3.5} \end{equation}\]

Inertia voidaan esittää rivien ja keskiarvorivin (sentroidin) \(\chi^{2}\) -etäisyyksien neliöiden painotettuna summana, jossa painoina ovat rivien massat \(m_{i}\) ja summa lasketaan yli rivien \({i}\).

\[\begin{equation} \phi^{2} = \sum_{i} (massa \: m_{i}) \times (profiilin \: i \: \chi^{2} - etäisyys \: sentroidista)^{2} \tag{3.6} \end{equation}\]

Korrespondenssianalyysin kolme peruskäsitteen “tripletti” – profiili, massa ja \(\chi^{2}\) - etäisyys – on esitelty. “Triplettiä” täydentää “kvartetti”, johon inertia kuuluu.

Rivi- ja sarakeprofiilien taulukoista huomaa, että keskiarvoprofiilien alkiot ovat massoja. Rivien keskiarvoprofiilin alkiot ovat sarakemassoja, ja sama pätee riveille. Tämä rivi- ja sarakeongelmien duaalisuus on yksinkertaisen korrespondenssianalyysin keskeinen idea (CAiP, s. 57). Rivi- tai sarakeongelman ratkaisu tuottaa saman tuloksen.

Ratkaisun dimensio on sarakkeiden tai rivien lukumäärä vähennettynä yhdellä, pienempi kahdesta vaihtoehdosta. Se on myös kokonaisinertian teoreettinen maksimi.

Korrespondenssianalyysi on läheistä sukua pääkomponenttianalyysille. Etäisyysmitta on khii2-etäisyys (käytän tekstissä tätä kirjoitusasua) ja tässä massat ovat mukana painoina. Ratkaisussa etsitään haluttu yleensä kaksiulotteinen ratkaisu (taso), joka minimoi pisteiden khii2-etäisyyksien poikkeamien summan eli on mahdollisimman lähellä pisteitä. Alkuperäisen täyden dimension (full space) data projisoidaan tälle tasolle.

3.2 Symmetrinen kartta

Korrespondenssianalyysi kuvaa taulukon riippuvuudet karttana. Symmetrinen kartta on yleisin ja useiden ohjelmistojen oletuskartta.

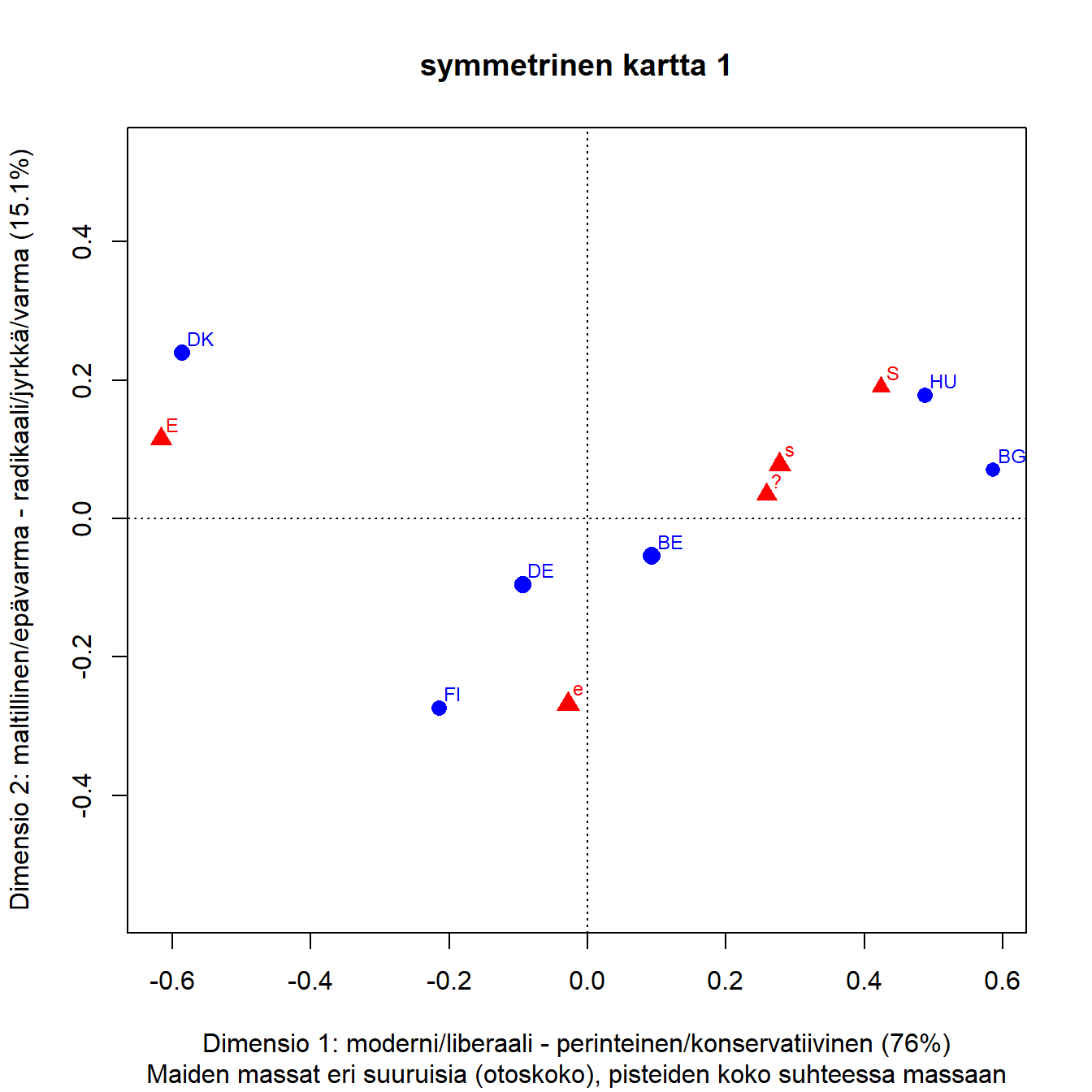
Kuva 3.3: Q1b: lapsi kärsii jos äiti on töissä

Akselien prosenttimerkinnät kertovat, kuinka paljon aineiston inertiasta eli hajonnasta on kaksiulotteisessa projektiossa saatu kuvattua akseleille.

Akselit ovat sisäkkäisiä (nested). Ensimmäinen akseli saa aina suurimman osan inertiasta, tässä 76 prosenttia. Kun toinen akseli kuvaa 15 prosenttia koko inertiasta, on kartalla esitetty 91 prosenttia aineiston hajonnasta. Loput 9 prosenttia jää 3. ja 4. dimensiolle. Nämä ”selitysosuudet” ovat samantapainen laskelma kuin perinteisen regressiomallin ”selitetty” vaihtelu ja ”jäännösvaihtelu”.

Akselien tulkinta on korrespondenssianalyysin perustehtävä. Kontrastit määrittävät akselien tulkinnan. Benzacrin ohjeen mukaan ( LeRoux ja Rouanet (2004), s.49) katsotaan mitä on oikealla ja mitä vasemmalla. Akselien tulkinta perustuu siihen, mitä yhteistä on kaikilla elementeillä, jotka ovat origon vasemmalla puolella ja vastaavasti origon oikealla puolella. Samalla tavalla tulkitaan toinen akseli, mitä on ylhäällä ja alhaalla. Tulkinta tehdään akseleiden suuntaan. Kuvan tulkintaa ei aloiteta pisteiden etäisyyksiä vertailemalla.

Kun taulukon rivit ovat havaintoja ja sarakkeet muuttujia, akselien tulkinta tehdään muuttujien avulla. Vasemmalla on E ja oikealla puolella samanmieliset vastaukset s ja S. Neutraali ”?” on s-vastausten vasemmalla puolella mutta kuitenkin oikealla. Kuvan perusteella ei voi sanoa kuinka paljon, kaikki erot ovat suhteellisia.

Sarakkeet ovat oikeassa järjestyksessä, mutta niiden koordinaatit x-akselilla eivät olen tasavälisiä. Jos muuttuja jostain syystä halutaan esittää välimatka- tai suhdeasteikon muuttujana koordinaatti ensimmäisellä dimensiolla on yksi vaihtoehto.

Ensimmäisen dimension tulkinta on aika selkeä. Toinen akseli on kontrasti lievemmän tai maltillisemman erimielisyyden (e) ja muiden vastausten kanssa. Se on 1. dimension suuntaan kaikkein lähimpänä origoa. Hieman varovaisemmin akselin voi tulkita maltillisen ja jyrkemmän tai varmemman mielipiteen kontrastiksi.

En jatkossa esitä kuvailevia akseleiden nimiä kuvissa, akseleiden tulkinta olisi kumminkin analyysin ensimmäinen tehtävä.

Maiden vertailu tehdään näiden akselien suuntaan. Sekä sarakepisteiden että rivipisteiden keskinäiset välimatkat approksimoivat optimaalisesti niiden khii2-etäisyyksiä. Sarake- ja rivipisteiden välisillä etäisyyksillä ei ole mitään suoraa tulkintaa. Pisteiden etäisyydet samassa pistepilvessä ovat suhteellisia, Saksa on konservatiivisempi kuin Suomi mutta emme tiedä kuinka paljon. Maiden järjestys oikealta vasemmalle on selkeä, Tanska on vasemmalla liberaalina ”ääripäänä”, oikealla taas Unkari ja Bulgaria. Pystyakselin suuntaan nähdään, että kaikkein ”maltillisin” mutta kuitenkin liberaali on Suomi, jyrkimmät mielipiteet löytyvät Unkarista ja Tanskasta.

Näitä tulkintoja voi vertailla edellä esitettyihin kahteen kuvaan rivi- ja sarakeprofiileista. Näkeekö niistä helposti saman riippuvuuden rakenteen? Kartta kertoo selvästi enemmän, mutta vaati ensin tulkinnan.

Kartta on approksimaatio neliulotteisen pistepilven hajonnalle. Vain origo on siinä tarkasti esitetty. Se on koko aineiston keskiarvopiste, ja pisteiden hajonta sen ympärillä kuvaa poikkeamaa riippumattomuushypoteesista.

Tärkeä geometrinen periaate on se, että kaukana on kaukana myös alkuperäisessä pistepilvessä, mutta kartalla lähellä olevat pisteet eivät välttämättä ole lähellä. Projektio kutistaa pisteiden etäisyyksiä.

Approksimaation laatu selviää korrespondenssianalyysin numeerisista tuloksista, samoin se miten rivi- ja sarakepisteen määrittävät akselit.

Kartoissa tärkein tekninen yksityiskohta on kuva- tai muotosuhde (aspect ratio). Akseleiden mittayksikön pitää olla sama eli muotosuhteen yksi. Jos kuvia tulostetaan useassa formaatissa kannattaa olla tarkkana. Kuvien on jo analyysivaiheessa oltava lukukelpoisia, ja symbolien kokoa joutuu isoissa aineistoissa säätämään. Tulosten esittäminen lopullisessa muodossa vaatii jo paljon vaivannäköä, tässä tutkielmassa esitetään vain datan analysoinnin valikoituja kuvia. Tutkielman karttojen ulkoasu ei ole paras mahdollinen, mutta tarkoitukseen riittävän hyvä. Graafinen data-analyysi on vaivatonta vasta sitten kun se tehty.

Vaatimukset datalle

Korrespondenssianalyysin sovelletaan yleisimmin frekvenssitaulujen analyysiin, lukumäärädataan (count data). Periaatteessa mikä tahansa data sopii, kunhan se voidaan järkevästi esittää suhteellisina lukumäärinä (relative amounts), siis suhdeasteikon (ratio scale) muuttujana. Tässä oleellista on tulkittavuus tutkimusongelman näkökulmasta. Välttämätön ehto on sama mittayksikkö: lukumäärä, rahayksikkö, pituusmitta kelpaavat (CAiP s. 15). Taulukon lukujen on oltava ei-negatiivisia (positiivisia, nolla sallittu).

Rajat ovat joustavia, kun mukaan otetaan erilaiset uudelleenskaalaukset ja transformaatiot. Tämä oli menetelmän perusidea jo Benzecrillä (CAiP, s. 201).

Menetelmää sovelletaan profiileihin, jotka painotetaan massoilla, ja profiilien etäisyyksiä mitataan khii2-etäisyysmitalla. Jos datan voi esittää tässä muodossa, menetelmää voi käyttää.

3.3 Asymmetrinen kartta ja ideaalipisteet

Symmetrisessä kartassa (Kuva 3.3) molemmat pisteparvet on esitetty pääkoordinaateissa (principal coordinates) ikään kuin päällekkäin, samassa kuvassa.

Toinen vaihtoehto on asymmetrinen kartta, jossa toinen pistejoukko esitetään standardikoordinaateissa ja toinen pääkoordinaateissa. Asymmetrisessä kartassa (Kuva 3.4) sarakkeet on esitetty standardikoordinaateissa ja rivit pääkoordinaateissa.

Sarakepisteitä kutsutaan ideaalipisteiksi, ne edustavat kuvitteellisia maita, joissa kaikki vastaukset ovat samoja. Matemaattisesti kartalle projisoidut ideaalipisteet ovat (tässä esimerkissä) neliulotteisen avaruuden verteksin (monikulmion) kärkipisteitä. Rivipisteet ovat tämän verteksin sisällä.

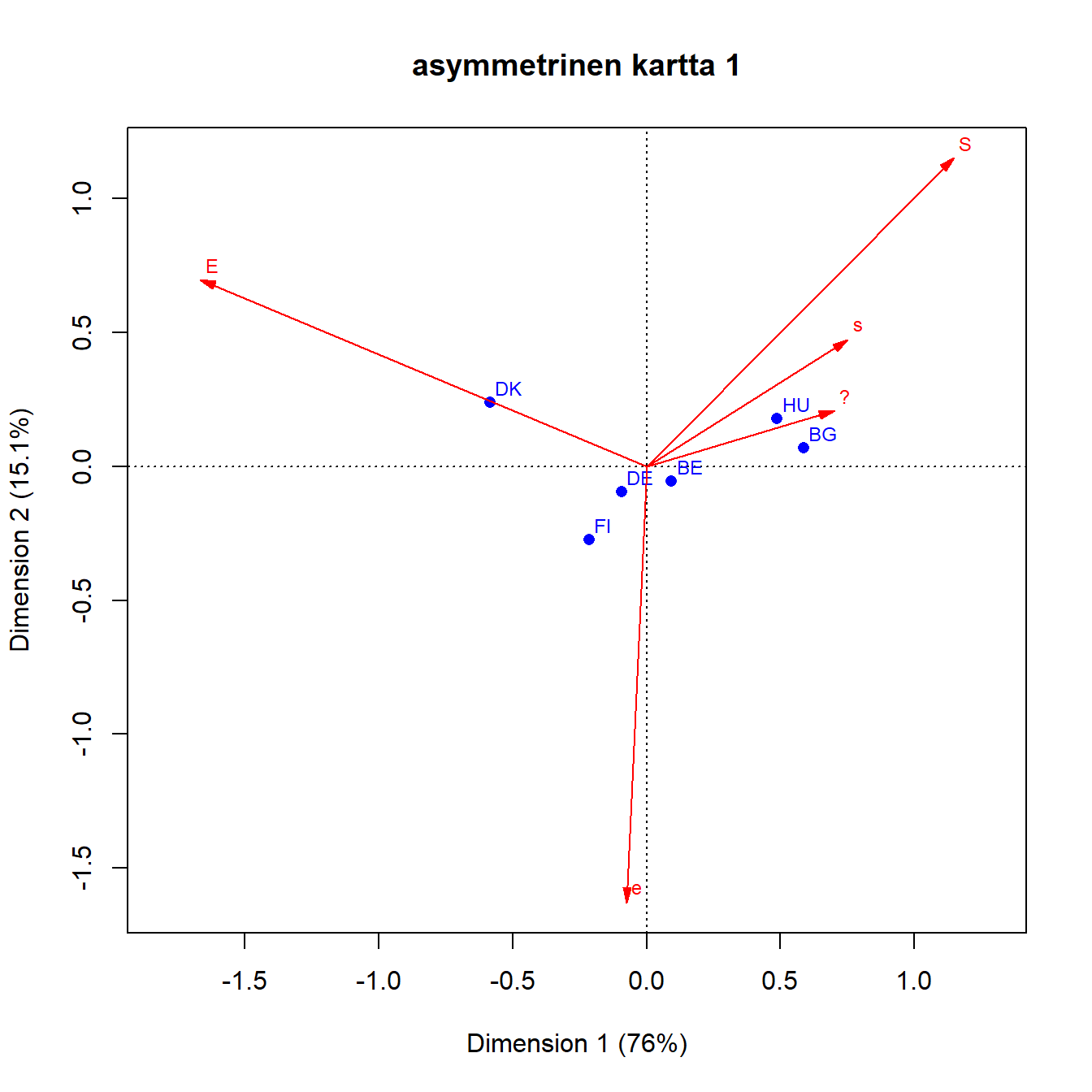
Kuva 3.4: Q1b: lapsi kärsii jos äiti on töissä

Sarakepisteet kuvaavat maksimi-inertiaa, ja rivipisteiden paljon pienempi hajonta kuvaa niiden poikkeamaa tästä hypoteettisesta tilanteesta. Sarakepisteet skaalautuvat origosta ulospäin. Asymmetrisessä kartassa rivi- ja sarakepisteiden etäisyydellä on tulkinta, samoin rivipisteiden välisellä etäisyydellä. Sarakepisteiden välisillä etäisyyksillä ei ole tulkintaa. Sarakepisteet on skaalattu ja mittakaavan ero symmetriseen karttaan näkyy selvästi.

Ideaalipisteiden tulkinnan voi varmistaa sarake kerrallaan, projisoimalla rivipisteet origon kautta piirretylle janalle. Kuvassa 3.5 nähdään mikä on maiden järjestys E-vastausvaihtoehdossa.

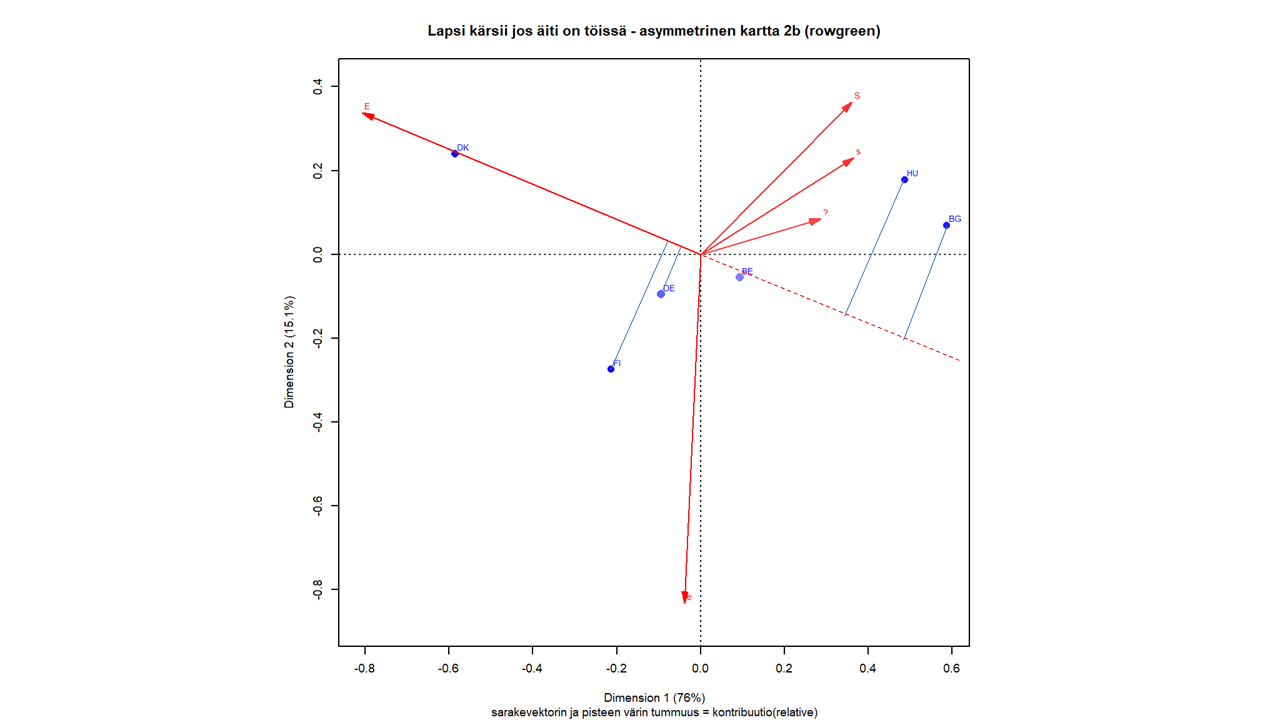
Kuva 3.5: Rivipisteiden projektiot

Asymmetrinen kartta antaa toisen näkökulman rivien ja sarakkeiden suhteeseen. Sen huono puoli on ideaalipisteiden karkaaminen kauas origosta ja rivipisteiden pakkautuminen pieneksi parveksi. Jos rivipisteiden hajonta on suuri, kuva on käytännöllinen. Kyselytutkimusaineistoissa näin ei yleensä ole.

3.4 Kontribuutiot kartalla

Kartassa (Kuva 3.3) on esitetty myös pisteiden massat. Tässä aineistossa pisteiden tai sarakesymbolien kokoerot eivät kovin selvästi erotu, mutta yleiskuvan ne kertovat.

Rivipisteiden ja sarakkeiden kontribuutiot voidaan esittää kartalla värisävyinä.

Kun kartalla pistejoukon inertia kuvataan akseleille, on jokaisella pisteellä oma osuutensa akseleiden kuvaamasta inertiasta. Absoluuttinen kontribuutio kertoo rivin tai sarakkeen osuuden akselin inertiasta. Vaikutuksessa on mukana pisteen massa.

Suhteellinen kontribuutio kertoo akselin osuuden pisteen inertiasta. Tämä tunnusluku kuvaa pisteen projektion laatua, kuinka hyvin se on kartalla esitetty.

Kontribuutiokartta on asymmetrinen kartta, jossa sarakevektorit on skaalattu kertomalla ne massojen neliöjuurilla. Näin sarakevektorit “kutistuvat” kohti origoa mutta vektorin pituus kertoo edelleen sen suhteellisen massan. Kartta sopii niin pienen kuin suuren inertian tilanteisiin (M. Greenacre 2006).

Absoluuttiset kontribuutiot

Absoluuttisten kontribuutioiden jakautumista akseleille voi varovaisesti päätellä sarakevektorin ja akseleiden välisistä kulmista. Mitä lähempänä sarakevektori on akselia, sitä suurempi on sen osuus akselin inertiasta. Samanlaisia päätelmiä voi tehdä myös rivipisteistä hahmottamalla niistä janan origoon.

Käsitteisiin palataan tarkemmin seuraavissa luvuissa ja teorialiitteessä, ja liian tarkkaan karttaa ei kannata tutkia. Numeeriset tulokset ovat yksityiskohdissa selkeämpiä.

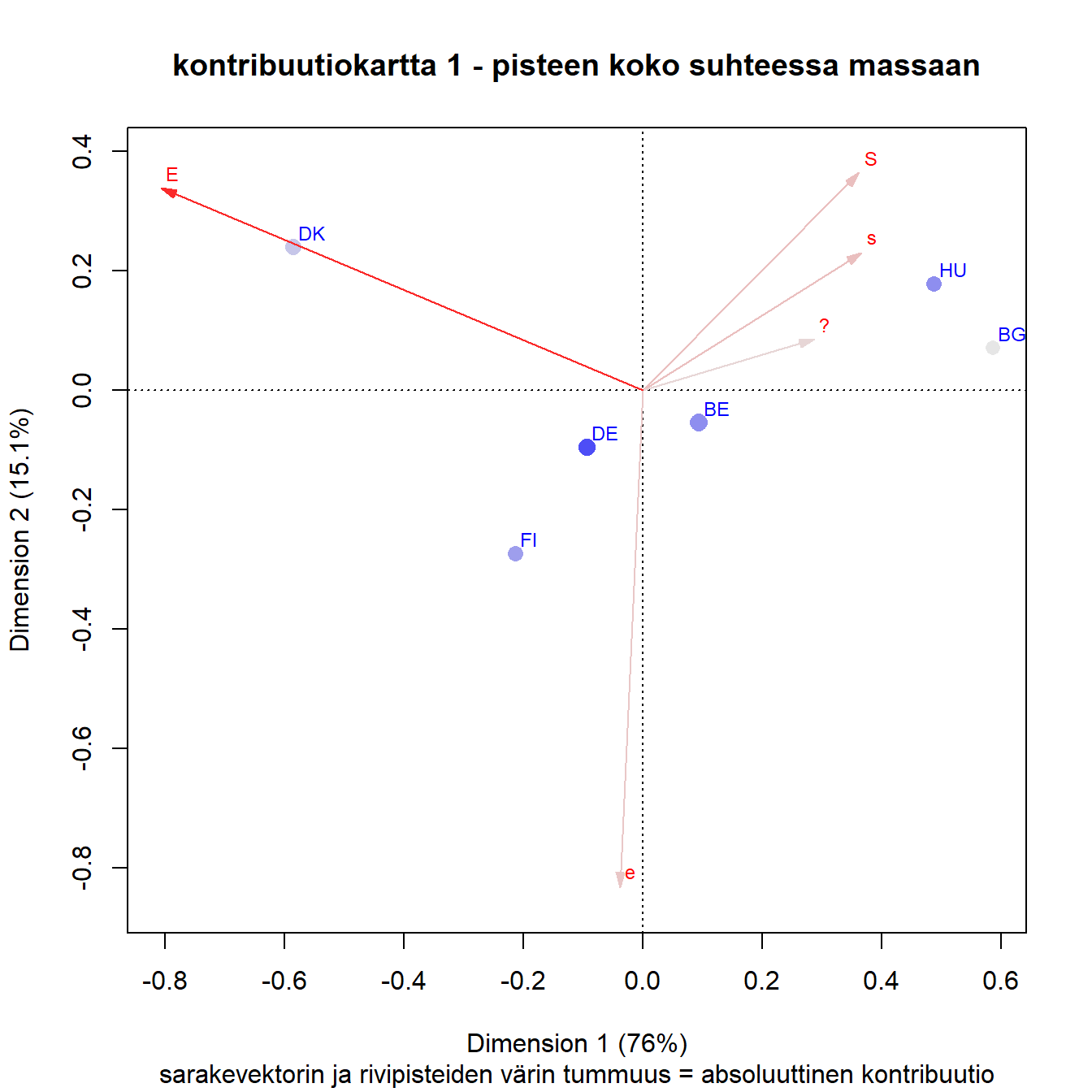
Kuva 3.6: Q1b: lapsi kärsii jos äiti on töissä

Sarakkeista ratkaisuun vaikuttaa selvästi eniten E, ja juuri ensimmäiseen dimensioon, joka selittää suurimman osan kokonaisinertiasta. Toista dimensiota määrittää vahvimmin e, mutta myös kaikki muut sarakkeet x-akselin yläpuolella. Samaa mieltä olevien (S ja s) vaikutus näyttäisi jakautuvan selvimmin molemmille dimensioille.

Vaikka massojen suhteellisia eroja ei kovin helposti pistekoosta erota, se näkyy epäsuorasti Saksan melko vahvana kontribuutiona. Bulgarian pieni kontribuutio näyttäisi olevan ensimmäiselle dimensiolle. Belgian kontribuutio ratkaisuun on pienempi kuin Saksan vaikka sen massa on hieman suurempi. Belgian ja Saksan pisteet ovat suhteellisesti lähempänä origoa jo suuren massansa ansiosta.

Suhteelliset kontribuutiot

Sarakkeiden laatu näyttäisi olevan hyvä, mutta rivipisteistä Saksa ja erityisesti Belgia erottuvat hieman heikommin esitettyinä.

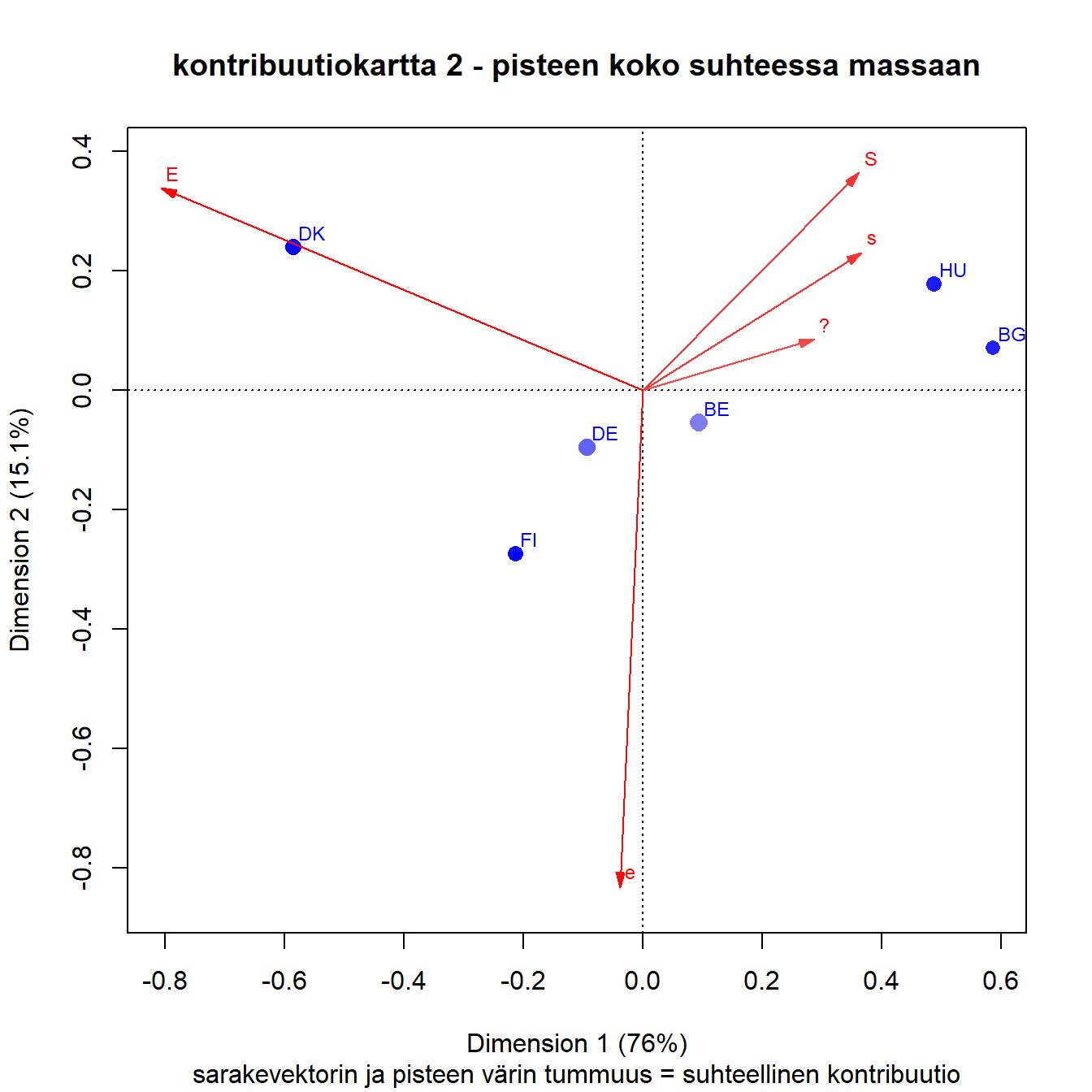
Kuva 3.7: Q1b: lapsi kärsii jos äiti on töissä

Massojen ja kontribuutioiden esittäminen kartoilla näyttää selkeimmin poikkeavat pisteet. Kontribuutioiden graafinen tarkastelu antaa myös yleiskuvan, jonka voi varmistaa numeerisista tuloksista.

Kaikki edellä esitetyt päättelyt perustuvat tietysti kaksiulotteiseen projektioon. Jos pisteet on esitetty hyvin eli niiden inertiasta (poikkeamasta keskiarvosta) suuri osa on kuvattu kartalle, rivipiste on sitä lähempänä ideaalipistettä mitä suurempi ideaalipisteen osuus on sen profiilissa.

3.5 Massat

Massat ovat korrespondenssianalyysin keskeinen käsite, ja niiden kaksoisrooli on menetelmässä tärkeä. Massat ovat normalisoiva muunnos khii2-etäisyysmitalle ja profiilien painoja.

Tässä jälkimmäisessä roolissa massat liittyvät tutkimusongelmaan, mitä halutaan vertailla? Kun vertaillaan eri maita, ei ole kovin perusteltua käyttää massoina eri maiden otoskokoja. Jos taas halutaan vertailla vaikkapa miesten ja naisten vastauksia on luonnollista normalisoida miesten ja naisten massat yhtä suuriksi. Rivi- ja sarakemassat ovat verrannollisia taulukon rivi- ja sarakesummiin, frekvenssitaulukon reunajakaumiin. Ne voidaan tutkimusongelmaan sopivalla tavalla skaalata uudelleen. Kun esimerkiksi vertaillaan viittä koulutustaso-ryhmää massat skaalataan verrannollisiksi niiden väestötason osuuksiin (CAiP, s. 23). Tällainen datan esikäsittely on normaali osa korrespondenssianalyysin soveltamista.

Jos massat halutaan vakioida osajoukoissa yhtä suuriksi, ratkaisu on yksinkertainen. Korrespondenssianalyysin taulukoksi otetaan riviprofiilitaulukko, jossa rivien summat ovat yksi.

Kuvassa 3.8 on tehty näin, ja kartta eroaa hämmästyttävän vähän maiden otoskokoja massoina käyttävästä kartasta 3.3.

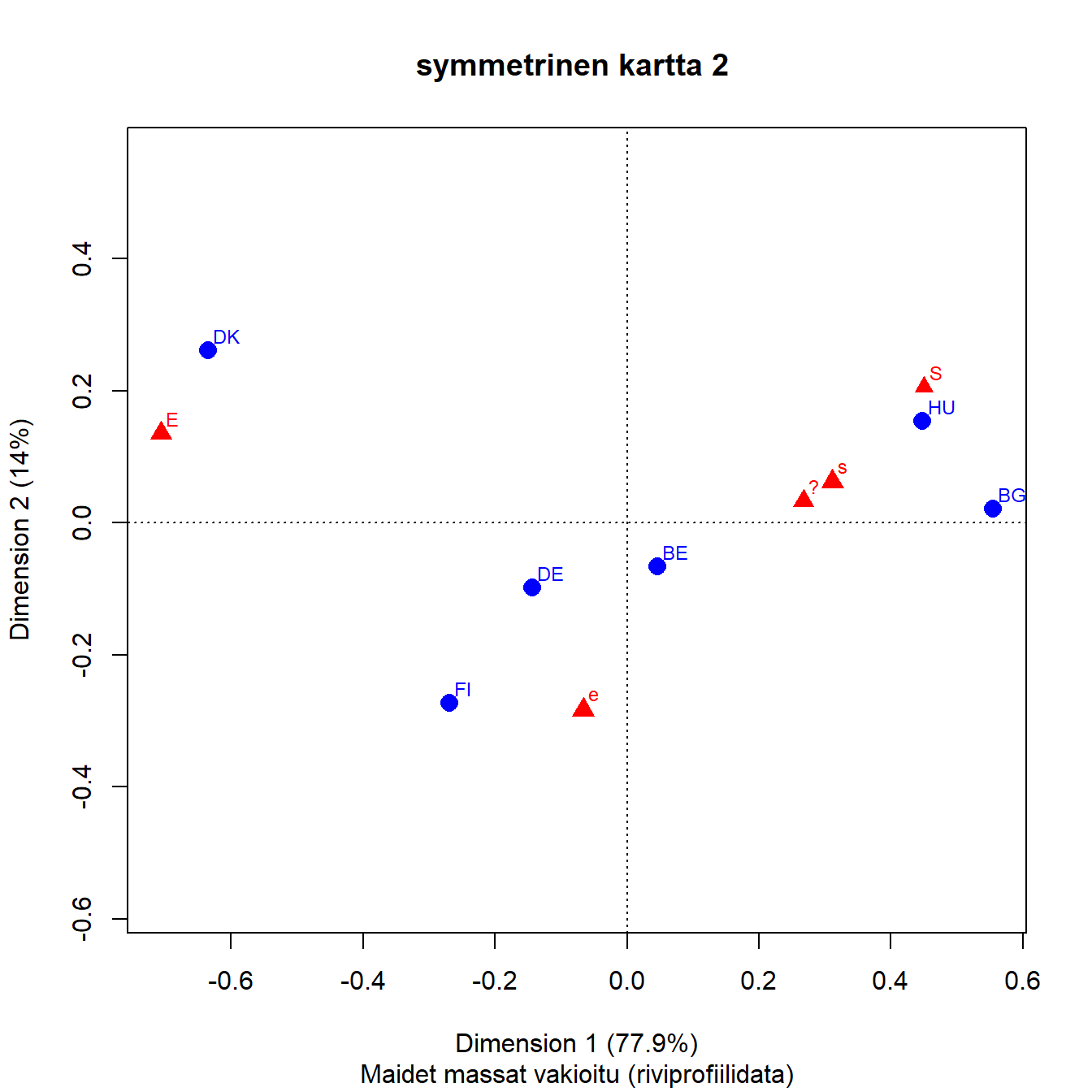
Kuva 3.8: Q1b: lapsi kärsii jos äiti on töissä

Pienimpien otosten maat (Bulgaria, Unkari) liikahtavat hieman origoa kohti, Bulgaria hieman enemmän kohti maltillista puolta y-akselin suuntaan.

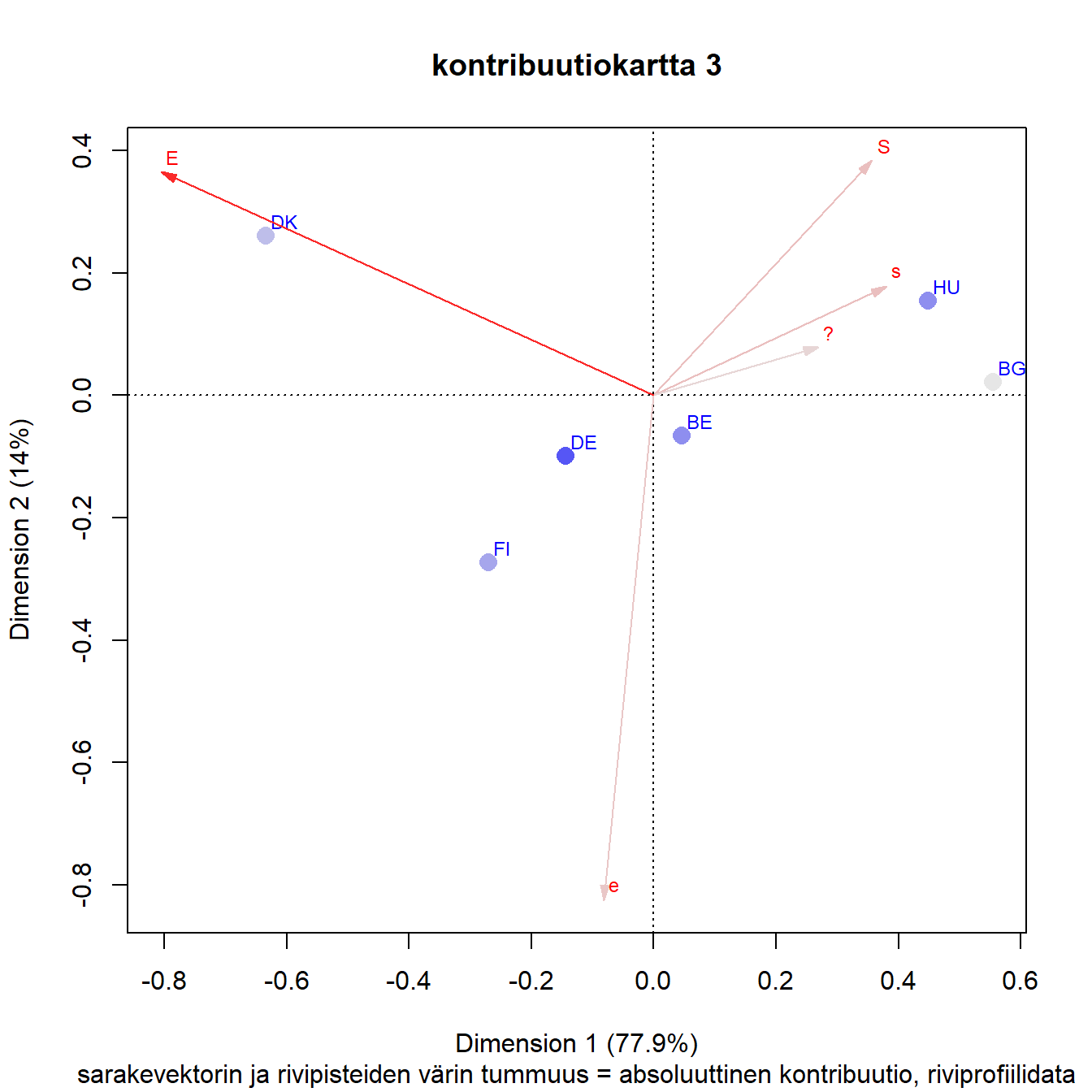
Kuva 3.9: Q1b: lapsi kärsii jos äiti on töissä

Kontribuutiokartta 3.9 ei juuri eroa edellä esitetystä kartasta 3.6.

En ole vakioinut vertailtavien ryhmien (tässä maat) suhteellisia osuuksia. Syy on yksinkertainen: esittelen menetelmää sen perusmuodossa ilman kovin täsmällisiä tutkimusongelmia. Oikeiden tutkimuskysymysten vastauksia pitää tietysti etsiä järkevillä massojen skaalauksella. Korrespondenssianalyysi on inertian dekomponointia, jakamista osiin.

3.6 Karttojen erot

Yksinkertaisen korrespondenssianalyysin peruskuva on symmetrinen kartta. Ehkä yllättäen sen “…tulkinta on edelleen menetelmän kaikkein kiistanalaisin aspekti” (CAiP s.295, M. Greenacre (2006)).

Sarake- ja rivipisteet esitetään siinä ikään kuin päällekkäin, samassa koordinaatistossa. Niiden pääkoordinaatit ovat kuitenkin eri pistejoukoista tai avaruuksista. Asymmetrisessä kartassa pisteet ovat samassa avaruudessa, ja ero on Greenacren mukaan vain skaalaus. Asymmetrisessä kartassa standardikoordinaateissa esitetyt ideaalipisteet skaalataan pääakselien suunnassa vastaavilla pääakselien inertioiden neliöjuurilla.

Kun akselien inertioiden (principal inertias) neliöjuuret eivät ole liian erisuuruisia, ideaalipisteiden suuntavektorit ovat lähes saman suuntaisia pääkoordinaateissa ja standardikoordinaateissa.

Jos pääinertioiden neliöjuuret ovat hyvin eri suuruisia, tulkintaongelmia voi tulla, mutta niillä ei käytännössä ole merkitystä. Siksi Greenacre pitää skaalausdebattia akateemisena kiistana, käytännön sovelluksissa sillä ei ole merkitystä. Greenacre (1989) kommentoi skaalausta perusteellisesti, kiista on ollut aika sitkeä mutta lienee laantunut.

Symmetrinen kartta on hyvä vaihtoehto, sillä asymmetrisessä kartassa skaalaus vie ideaalipisteet usein kauas ja pääkoordinaateissa esitetyt pisteet pakkautuvat kuvan keskelle. Jos dataa tulkitaan asymmetrisesti kontribuutiokartta on hyvä vaihtoehto. Silloin rivipisteiden khii2-etäisyydet esitetään optimaalisesti ja sarakkeiden suuntavektoreille projisoiduilla pistellä on kaksoiskuvatulkinta.

Greenacren mukaan kartoilla voi tavoitella kolmea eri asiaa. Kuvassa voi esittää rivipisteiden etäisyydet, sarakepisteiden etäisyydet tai rivi- ja sarakepisteiden etäisyydet. Jälkimmäinen on kaksoiskuvien (biplot) ns. skalaaritulo-ominaisuus. Rivi- ja sarakepisteen skalaaritulo “palauttaa” alkuperäisen datan, tässä tapauksessa taulukon solun.

Edellä mainituista tavoitteista vain kaksi voidaan optimaalisesti esittää yhtä aikaa.

Symmetrisessä kartassa khii2-etäisyydet rivipisteiden välillä ja sarakepisteiden välillä esitetään optimaalisesti. Rivi- ja sarakepisteiden välisiä etäisyyksiä ei esitetä optimaalisesti, mutta ne voidaan tulkita kohtalaisen hyvin, jos pääakselien inertioiden neliöjuuret eivät ole liian erisuuruisia.

Asymmetrisessä kartassa pääkoordinaateissa esitetyn pistejoukon etäisyydet kuvataan optimaalisesti, standardikoordinaateissa esitetyt pisteet ovat “ääriprofiileja”, verteksin kulmapisteitä. Rivi- ja sarakepisteiden etäisyydet esitetään optimaalisesti, mutta sarakepisteiden etäisyyksillä ei ole suoraa tulkintaa,

Kontribuutiokartta on muunnelma asymmetrisestä kartasta. “Ääriprofiilit” vedetään kohti origoa kertomalla ne massojen neliöjuurilla. Näin kuva selkenee, ja “kutistetun” pisteen etäisyys origosta kertoo sen kontribuution pääakseleille. Näiden pisteiden välisillä etäisyyksillä ei ole suoraa tulkintaa.

Jako standardi- ja pääkoordinaatteihin on suora seuraus korrespondenssianalyysin matemaattisesta ratkaisusta. Greenacre esittelee kaksoiskuvia käsittelevässä kirjassaan (Greenacre 2010) selkeästi koordinaattien yhteyden ratkaisualgoritmiin, singulaariarvohajotelmaan.

Koordinaattien yhteys voidaan esittää kahtena yksinkertaistettuna kaavana (M. Greenacre ja Primicerio (2013), s.174):

\[\begin{equation} pääkoordinaatit = standardikoordinaatit \times \sqrt{pääakselien \: inertiat} \tag{3.7} \end{equation}\]

\[\begin{equation} kontribuutiokoordinaatit = \sqrt{massat} \times standardikoordinaatit \tag{3.8} \end{equation}\]

Luku 4 Täydentävät pisteet

Edellisessä luvussa kuviin listättiin informaatiota värisävyinä (kontribuutiot) ja rivi- ja sarakepisteiden kokoa muuntelemalla (massat). Täydentävät pisteet (supplementary points,CAiP s. 89-) ovat rivejä tai sarakkeita, jotka lisätään karttaan. Mikä tahansa rivi tai sarake voidaan lisätä kuvaan, jos se on järkevästi vertailukelpoinen kartan määrittäneiden profiilien kanssa.

Tällainen piste on kartan laskennassa passiivinen, sillä on sijainti kartalla mutta ei massaa eikä vaikutusta inertiaan. Passiivisilla pisteillä ei ole vaikutusta (kontribuutiota) kartan pääakseleihin.

Täydentävillä pisteillä on kolme yleistä käyttötarkoitusta. Kartalle voidaan lisätä profiili, joka on jollain lailla sisällöllisesti erilainen kuin muut. Esimerkkiaineistossa kartalle voisi lisätä joitain Euroopan ulkopuolisia maita. Vaikka nämä riviprofiilit eivät vaikuta kartan akseleiden määräytymiseen, ne voidaan esittää kuuden maan määrittämässä “avaruudessa”. Projektion laatu (suhteelliset kontribuutiot) voidaan myös esittää.

Toinen käyttötapaus on pienen massan profiili. Tällaisella pisteellä voi olla iso vaikutus ratkaisuun, mutta passiivisena pisteenä se sijoitetaan muiden pisteiden määrittämälle kartalle. Jo sisällöllisistä syistä pienen massan pisteiden esitystä kannattaa harkita, ne sijaitsevat kaukana origosta ja huonontavat kuvan laatua.

Kolmas mahdollisuus on jakaa pistejoukkoja osajoukkoihin ja esittää niiden summaprofiili täydentävänä pisteenä. Summaprofiili on osiensa painotettu (barysentrinen) keskiarvo. Kun se esitetään passiivisena pisteenä, havaintoja ei oteta ratkaisuun kahta kertaa. Profiilien yhdistämiseen liittyy korrespondenssianalyysin tärkein ominaisuus, jakaumaekvivalenssi (distributional equivalence). Se on ollut menetelmän kehittämisen tärkein tavoiteltu ominaisuus. Profiileiltaan samanlaiset rivit voidaan yhdistää, analyysin tulokset eivät muutu. Khii2-etäisyysmitta on ainoa etäisyysmitta, joka toteuttaa tämän periaatteen.

LeRoux ja Rouanet (2004) esittelevät menetelmän matemaattiset perusteet ja jakaumaekvivalenssin perusteellisesti. Havainnollinen esitys löytyy Greenacren oppikirjasta (CAiP).

Täydentävien profiilien lisääminen vaatii jo yksinkertaisia matriisioperaatioita. Korrespondenssianalyysi on käytännössä matriisien muokkausta tutkimusongelman tarpeisiin.

4.1 Saksan ja Belgian alueet

Saksan ja Belgian aineistossa on mukana aluejako: entiset Itä- ja Länsi-Saksa (dE,dW), Flanderi (bF), Vallonia (bW) ja Bryssel (bB).

Taulukko 4.1: Q1b vastaukset, Saksan ja Belgian alueet
	S	s	?	e	E	Total
bF	5.04	23.81	25.89	30.83	14.43	100.00
bW	10.82	21.02	18.57	24.08	25.51	100.00
bB	17.03	20.94	16.63	23.87	21.53	100.00
BG	12.81	42.89	22.26	20.63	1.41	100.00
dW	11.40	26.82	11.83	32.13	17.82	100.00
dE	5.85	11.33	10.97	29.80	42.05	100.00
DK	5.04	17.15	10.95	16.71	50.14	100.00
FI	4.23	16.94	13.42	38.11	27.30	100.00
HU	21.97	28.89	22.57	19.06	7.52	100.00
All	9.95	23.76	16.79	26.10	23.41	100.00

Aineistoon lisätään passiiviisina riveinä Saksan ja Belgian maaprofiilit (DE, BE). Maiden massoja ei skaalata yhtä suuriksi, otoskoot vaikuttavat ratkaisuun.

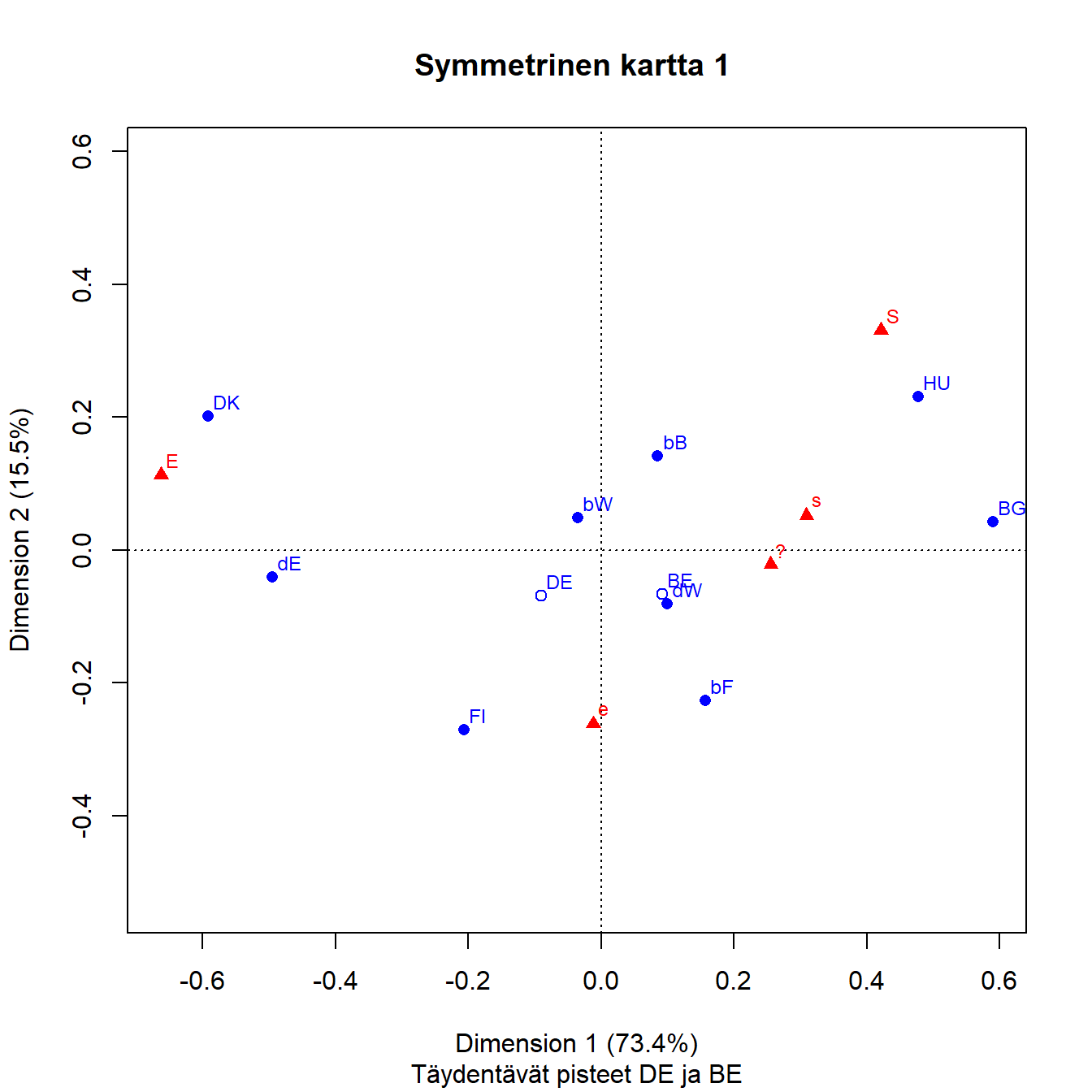
Kuva 4.1: Q1b: Saksan ja Belgian aluejako

Saksan ja Belgian täydentävät pisteet ovat osiensa barysentrisiä keskiarvoja, etäisyys on sitä pienempi mitä suurempi on osuus. Saksan piste sijaitsee siksi lähempänä Länsi-Saksan pistettä. Jos karttaa vertaa kuvaan 3.3 ei eroja juuri ole. Saksan ja Belgian osien sijoittuminen on kiinnostava. Itäinen Saksa on selvästi liberaalilla puolella, ensimmäisellä dimensiolla lähinnä Tanskaa. Läntinen Saksa on ensimmäisellä dimensiolla konservatiivisella puolella Belgian maapisteen tasolla. Belgian alueista Vallonia (bW) on liberaalilla puolella mutta kaikkein eniten oikealla. Bryssel ja Flanderi ovat konservatiivisella puolella, toinen Länsi-Saksaa liberaalimpi ja toinen konservatiivisempi. Belgian osat hajoavat toiseen suuntaan kuin Saksan, liberaalein Flanderi on myös kaikkein maltillisin ja Bryssel vastaavasti tiukempien mielipiteiden puolella. Sarakepisteiden suhteelliset sijainnit toisiinsa nähden eivät oleellisesti muutu.

Bryssel ja Vallonia näyttävä olevan hyvin lievästi U-muotoisen maapisteiden parven sisällä. Tämä kaariefekti tai Guttman-efekti on kartoissa yleinen. Se on tavallaan ratkaisun geometriasta. Rivipisteiden pilvi on sarakkeiden ideaalipisteiden virittämän verteksin sisällä, ja ainoa reitti verteksin kulmasta toiseen kulkee tasolla kaarevasti (CAiP, s. 127). Voi myös sanoa, että kaariefektin taustalla on järjestysasteikon muuttujan korrelaatio ((LeRoux ja Rouanet 2004), s. 220). Kaaren sisäpisteet ovat usein polarisoituneita ensimmäisen dimension “ääripäävastausten” välillä. Tässä vaikutus on heikko, taulukossa 4.1 ei mitään selvää polarisaatiota näy.

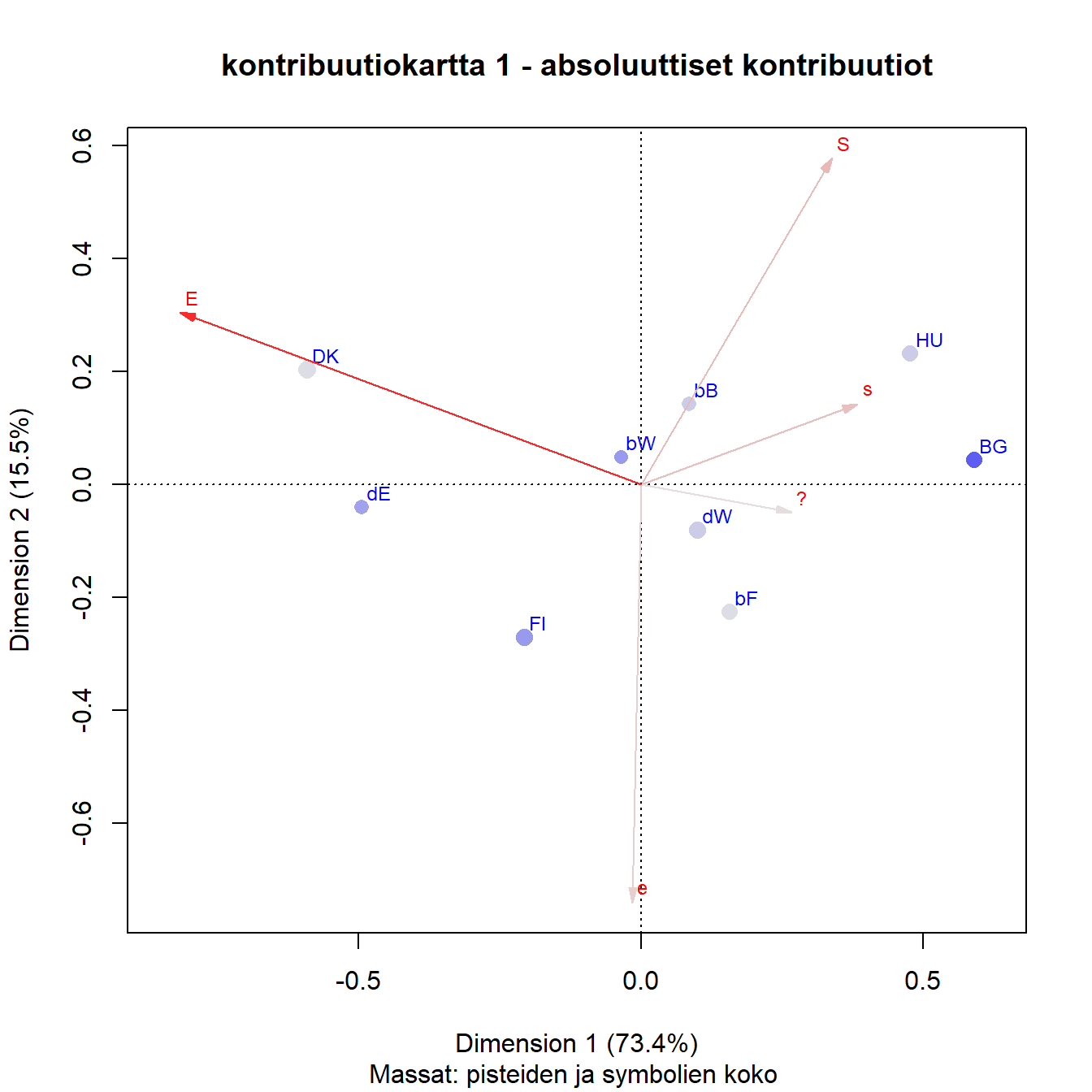
Kuva 4.2: Q1b: Saksan ja Belgian aluejako

Kontribuutiokartasta täydentävät pisteet on jätetty pois, ne eivät vaikuta ratkaisuun. Saksan ja Belgian osien massat ovat tietenkin pienempiä.

Sarakkeiden kontribuutiot ovat samantapaiset kuin alkuperäisessä kartassa 3.6. Rivipisteiden kontribuutioista osa on selvästi pienempiä, erityisesti Länsi-Saksa kaksi Belgian aluetta (bB, bF). Kuvan perusteella ei voi sanoa johtuuko tämä pelkästään massojen pienentymisestä.

Unkarin ja Bulgarian kontribuutiot muuttuvat eri suuntiin, Unkarin pienenee ja Bulgarian kasvaa.

4.2 Korrespondenssianalyysin numeeriset tulokset

Korrespondenssianalyysin numeeriset tulokset ovat tärkeitä tulkinnan varmistamiselle ja antavat tarkemman kuvan ratkaisusta. Nämä tulokset ovat erilaisia kokonaisinertian dekomponointeja. Kokonaisinertia (total inertia) profiilien ja keskiarvoprofiilin khii2-etäisyyksien massoilla painotettu summa (kaava (3.6)). Se kuvaa profiilipisteiden hajontaa ideaalipisteiden verteksin sisällä. Maksimi-inertia saavutetaan kun profiilit ovat verteksien kärkipisteissä, jokaisessa profiilissa on vain yksi luokittelumuuttujan arvo. Inertia on sama kuin ratkaisun dimensio, tässä esimerkissä 4 (sarakkeiden lukumäärä - 1). Numeeristen tulosten esittelyn tärkein lähde on CAiP, luku 11 ja liite B.

R-paketti “ca” listaa numeeriset tulokset suppeasti (print) ja laajemmin (summary). Alla on laajempi tulostus tutkielman esimerkin tilanteesta.

Ensimmäisenä on listattu kokonaisinertia pääakseleittain. Tässä suhteelliset luvut on esitetty prosentteina. Muut luvut on luettavuuden vuoksi skaalattu, joko kerrottu tuhannella tai esitetty “permills” (summa on 1000).

## 
## Principal inertias (eigenvalues):
## 
##  dim    value      %   cum%   scree plot               
##  1      0.154101  73.4  73.4  ******************       
##  2      0.032489  15.5  88.9  ****                     
##  3      0.014294   6.8  95.7  **                       
##  4      0.008944   4.3 100.0  *                        
##         -------- -----                                 
##  Total: 0.209828 100.0                                 
## 
## 
## Rows:
##       name   mass  qlt  inr    k=1 cor  ctr    k=2 cor  ctr  
## 1  |    bF |  124  650   69 |  157 212   20 | -226 438  195 |
## 2  |    bW |   60  388    3 |  -36 137    0 |   48 252    4 |
## 3  |    bB |   63  481   17 |   85 127    3 |  142 354   39 |
## 4  |    BG |  113  878  215 |  590 874  255 |   43   5    6 |
## 5  |    dW |  143  345   33 |  100 208    9 |  -81 138   29 |
## 6  |    dE |   67  966   82 | -495 960  107 |  -41   7    3 |
## 7  |    DK |  170  971  327 | -591 869  387 |  202 102  214 |
## 8  |    FI |  136  957   79 | -206 352   38 | -271 605  307 |
## 9  |    HU |  122  927  177 |  477 751  181 |  231 176  201 |
## 10 | (*)BE | <NA>  512 <NA> |   92 338 <NA> |  -66 173 <NA> |
## 11 | (*)DE | <NA>  418 <NA> |  -90 265 <NA> |  -68 153 <NA> |
## 
## Columns:
##     name   mass  qlt  inr    k=1 cor ctr    k=2 cor ctr  
## 1 |    S |   99  816  167 |  421 505 115 |  331 311 335 |
## 2 |    s |  238  781  143 |  309 759 147 |   52  22  20 |
## 3 |      |  168  594   88 |  255 589  71 |  -22   4   2 |
## 4 |    e |  261  871   98 |  -12   2   0 | -262 870 550 |
## 5 |    E |  234  999  505 | -663 971 667 |  113  28  93 |

Rivi- ja sarakeprofiileista esitetään samat tiedot. Ensimmäisessä kolmen sarakkeen joukossa kerrotaan pisteen massa, laatu (qlt) ja inertiakontribuutio.

Inertiakontribuutio (inr) on suhteellinen osuus kokonaisinertiasta. Aktiivisia rivejä on 9, joten tasaisesti jaettu inertia olisi noin 110. Tanska, Bulgaria ja Unkari “selittävät” suurimman osan inertiasta. Belgian ja Saksan alueiden kontribuutiot ovat pieniä. Nämä inertiaosuudet ovat osuuksia kokonaisinertiasta alkuperäisessä neljässä ulottuvuudessa.

Laatu kertoo, miten hyvin piste on esitetty kartalla, miten suuri osa sen inertiasta on esitetty kartalla. Pisteen inertia on sen massalla painotettu poikkeama aineiston keskiarvosta, ja jos tämä poikkeama saadaan kartassa näkymään piste on esitetty hyvin.

Kaksiulotteinen kartta, kuten tässä, on yleisin valinta, laatu kerrotaan valitulle dimensioiden määrälle. Laatu ei riipu massasta, vaan pisteen ja kartan akseleiden välisistä kulmista (kts. teorialiite). Saksan osien ero laadussa on iso, Itä-Saksalla se on erittäin hyvä ja Länsi-Saksalla huono. Belgian alueista Vallonia on huonoimmin esitetty, ja vain Flanderin laatu on kohtuullisen hyvä. Kovin hyvä ei ole täydentävien maapisteidenkään laatu.

Kaksi seuraavaa kolmen sarakkeen ryhmää kertovat tulokset valituille dimensioille eli ratkaisulle. Molempien dimensioiden (“k=1”, “k=2”) pääkoordinaattien (x 1000) lisäksi raportoidaan dimension suhteellinen kontribuutio pisteen inertiaan (“cor”). Nämä tunnusluvut summautuvat laaduksi (qlt), ja ne voidaan tulkita korrelaation neliöiksi (kts. teorialiite).

Erityisesti Belgian alueiden projektion laatu on huonompi ensimmäisellä dimensiolla. Itä-Saksa ja Bulgaria taas ovat hyvin esitettyjä vain ensimmäisellä dimensiolla eivätkä juuri ollenkaan korreloi toisen dimension kanssa.

Pisteen absoluuttinen kontribuutio kertoo sen osuuden dimension inertiasta (summa 1000). E-sarake “selittää” ensimmäisen dimension inertiasta noin 66 prosenttia, ja dimensio saman verran kokonaisinertiasta. Absoluuttinen kontribuutio riippuu massasta ja siitä paljonko piste poikkeaa koko aineiston keskiarvopisteestä.

Numeerisista tuloksista voidaan varmistaa akseleiden tulkinta sarakkeiden avulla. Sarakkeet ovat hyvin esitettyjä tasossa, ainoastaan neutraali vaihtoehto on heikommin kuvattu, mutta sillä ei ollut roolia tulkinnassa.

E-sarakkeen vaikutuksen suunta ensimmäisellä dimensiolla näkyy pääkoordinaatin etumerkistä (k1 = -663), ja sen kontrastina ovat S- ja s- sarakkeet positiiviseen suuntaan. Toinen dimensio on kontrasti S- ja e-sarakkeiden välillä ja ne selittävät akselin inertian. Kaikki tämä voitiin päätellä kuvasta, ja numeeriset tulokset vahvistavat tulkinnan. Sarake S on ainoa, jonka kontribuutio on merkittävä molemmille dimensioille.

Jos pisteen kontribuutio akselille on iso, akselin suhteellinen kontribuutio (cor) pisteen inertiaan on suuri. Kääntäen tämä ei päde, piste voi olla akselilla hyvin esitetty mutta kontribuutio on silti pieni.

4.3 Esimerkki kolmiulotteisesta kartasta

Belgian ja Länsi-Saksan pisteet on esitetty huonosti kaksiulotteisella kartalla. Kolmiulotteinen ratkaisu näyttää miten ne sijoittuvat kolmannen akselin suunnassa. Tässä tarkastelu on vain diagnostiikkaa. Toisenlainen esimerkki on tutkimus Ranskan politiikan dimensiosta (“French political space”) 1990-luvun lopulla (LeRoux ja Rouanet 2004, 365). Siinä Ranskan poliittiset puolueet sijoitetaan kolmelle sisällöllisesti perustellulle dimensiolle.

Kolmannen dimension hajonnan voi esittää kahtena karttana.

Ensimmäisen ja kolmannen dimension kuvassa (Kuva 4.3) näkyy pisteparven hajonta tärkeimmän dimension ympärillä. Sarakepisteiden järjestys säilyy samana, samoin maapisteiden oikealta vasemmalle. Kaikki pisteet paitsi Vallonia hajoavat kolmannen akselin suuntaan. Belgian kahden pisteen (bB ja bF) eron havaitsee helposti, samoin Unkarin ja Bulgarian.

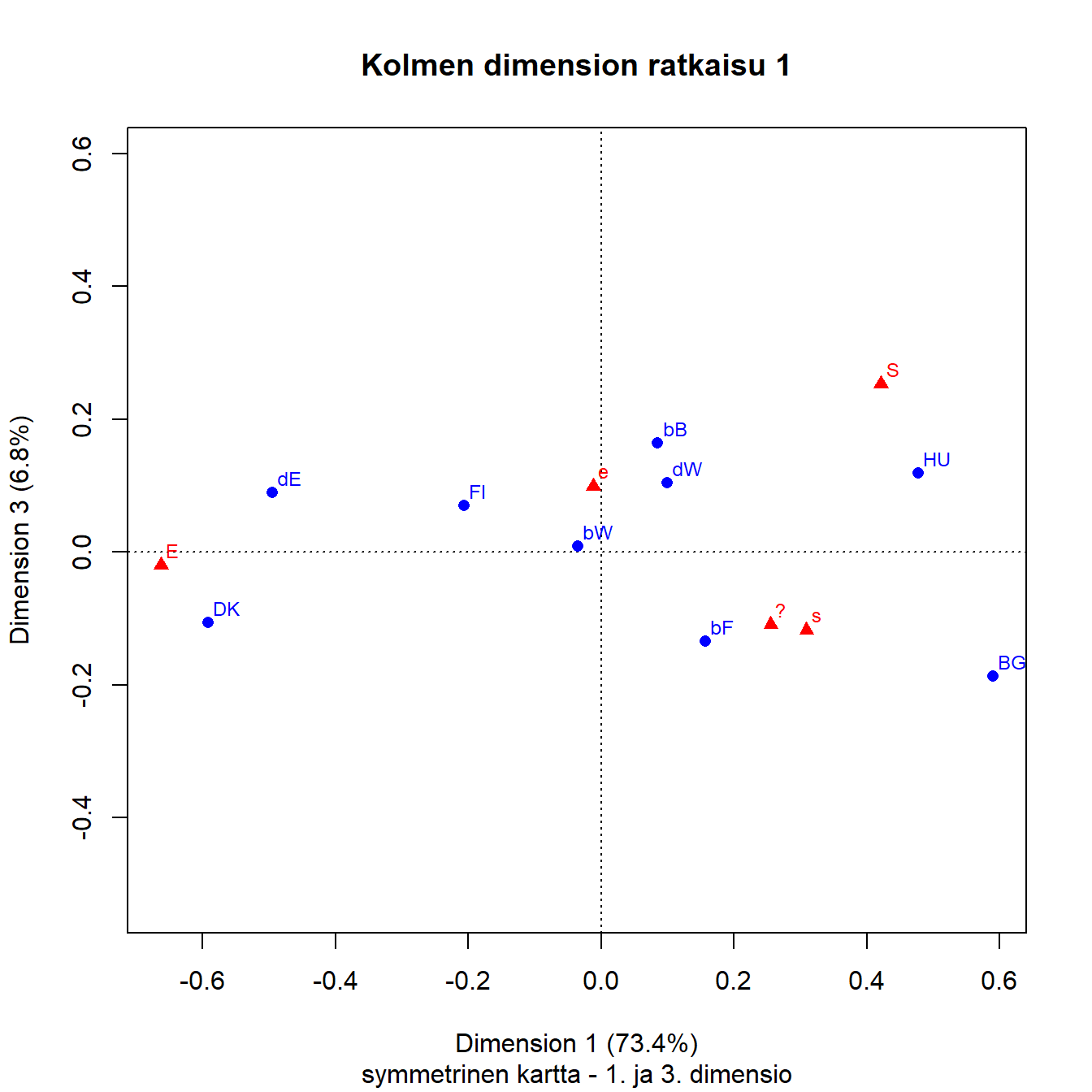
Kuva 4.3: Q1b: Saksan ja Belgian aluejako

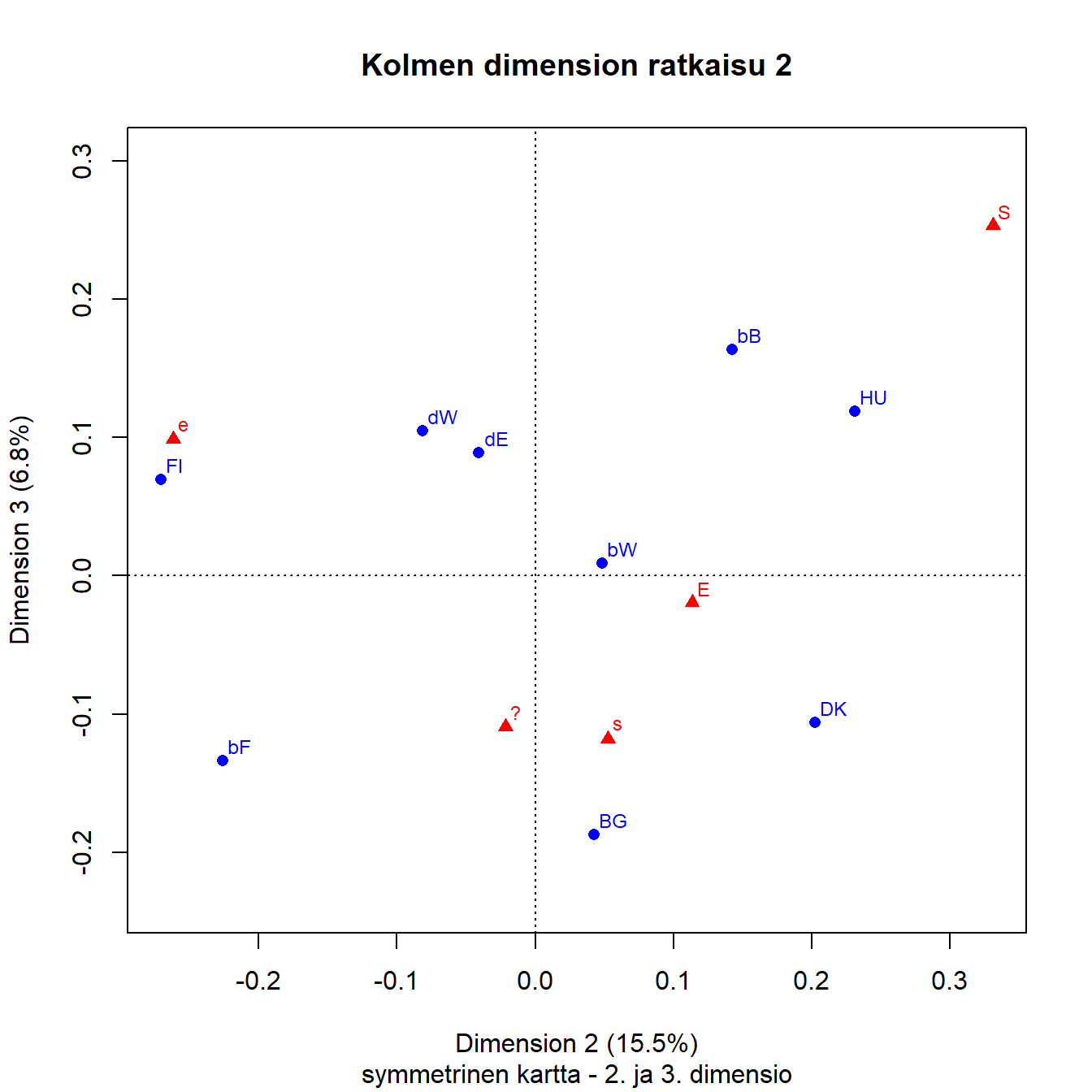
Kuva 4.4: Q1b: Saksan ja Belgian aluejako

Toisen ja kolmannen dimension kartalla (Kuva 4.4) on esitetty noin viidesosa kokonaisinertiasta. Tässäkin kuvassa Brysselin (bB) ja Unkarin pisteet ovat kontrastina Flanderin, Bulgarian ja Tanskan pisteille.

Diagnostisessa tarkastelussa on helpompaa käyttää dynaamisia kolmiulotteisia kuvia. R-ympäristössä saa grafiikkaikkunaan tulostettua kolmiulotteisen kuvan, jota voi käännellä ja katsoa eri kulmista. Näin saa paljon helpommin käsityksen kolmannen dimension hajonnasta.

Tässä on tyydyttävä kahteen kuvakaappaukseen (ks. alla kuvat 4.5 ja 4.6).

Kuva 4.5: Saksan ja Belgian aluejako - 3d-kuva1

Kuva 4.6: Saksan ja Belgian aluejako - 3d-kuva2

Miten kaksiulotteisessa kartassa huonosti esitettyjen pisteiden analyysiä voisi jatkaa? Siihen nämä kartat eivät suoraan anna mitään vastausta. Vaihtoehtoisia tapoja esitellään seuraavissa luvuissa.

Luku 5 Yhteisvaikutusmuuttujat

Yksinkertaisin tapa tutkia taustamuuttujien yhteisvaikutuksia on yhdistää kaksi muuttujaa uudeksi luokittelumuuttujaksi (“interactive coding”). Miehet ja naiset on seuraavaksi luokiteltu kuuteen ikäluokkaan (1=15-25, 2 =26-35, 3=36-45, 4=46-55, 5=56-65, 6= 66 tai vanhempi).

Poikkileikkausaineistossa vastaajan ikä kertoo myös ikäluokan (kohortin). Vastaajat ovat kokeneet kaksi suurta mullistusten vuotta elämänsä eri vaiheissa. Kaksi nuorinta ikäluokkaa on ollut 1990 alle 14-vuotiaita ja vanhin ikäluokka yli 44-vuotiaita. Finanssikriisin vuonna 2008 toiseksi nuorin ikäluokka on ollut 22-31 vuotiaita, ja kaksi vanhinta yli 51-vuotiaita. Pelkän ikävaikutuksen analyysi edellyttäisi vähintään kahden aineiston yhdistämistä.

Kolmen muuttujan yhteisvaikutusmuuttajaan yhdistän vastaajan maan. myös maa. Käytännössä kolmen luokittelumuuttujan yhdistäminen tekee taulukosta jo huteron, joissain soluissa havaintojen määrä pienenee. Kaikissa soluissa on sentään viisi havaintoa tai enemmän. Pienten massojen profiilien ja harvinaisten kategorioiden vaikutukset on kuitenkin arvioitava, ne voivat joskus, mutta onneksi harvoin, määrittää sitä liikaa.

5.1 Ikä ja sukupuoli

Ikäjakauma painottuu kaikissa maissa jonkin verran vanhempiin ikäluokkiin. Nuorempien ikäluokkien osuus on (alle 26-vuotiaat ja alle 26-35 - vuotiaat) varsinkin Bulgariassa (BG) ja Unkarissa (HU) pieni.

Ikäluokilla on luonnollinen järjestys, niiden pisteet voidaan yhdistää nuorimmasta vanhimpaan.

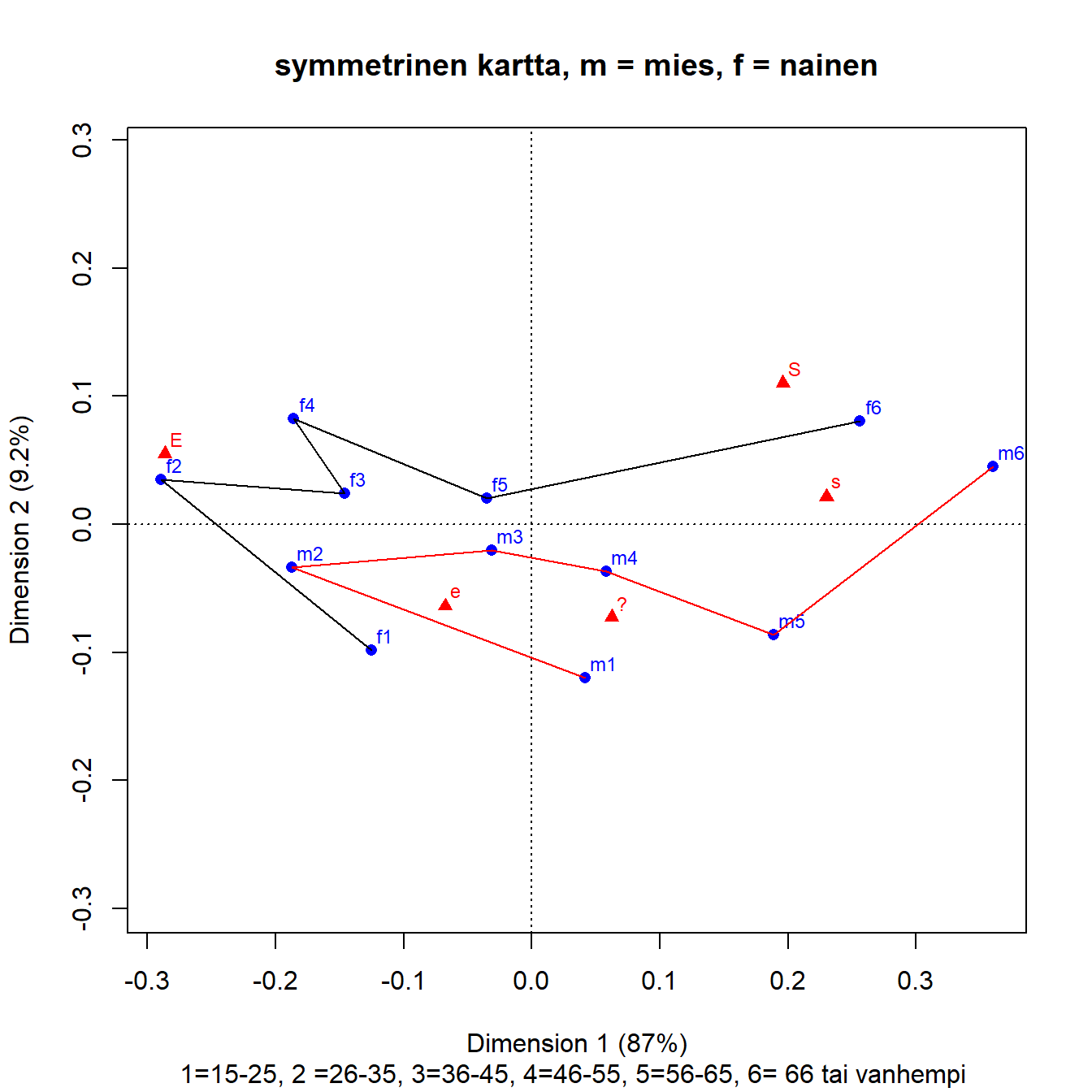
Kuva 5.1: Q1b: ikäluokka ja sukupuoli

Ratkaisu on melko yksiulotteinen, ensimmäinen dimensio kuvaa 87 prosenttia kokonaisinertiasta. Dimensioiden tulkinta on suurin piirtein sama kuin edellisissä kartoissa, mutta S-sarake on kiusallisesti s-sarakkeen vasemmalla puolella. Numeerisista tuloksista näkee (ks. tuloste alla), että sarakkeiden s ja E osuus kokonaisinertiasta (sarake inr) on 768. Niiden kontribuutio x-akselille on yhteensä vielä suurempi (849). Muut sarakkeet taas kontribuoivat y-akselin inertiaan, mutta sen osuus kokonaisinertiasta on vain 9 prosenttia. Kun sarakkeet kuitenkin ovat aika hyvin esitettyjä (qlt), voidaan x- akseli tulkinta hieman karkeammin samaa mieltä - eri mieltä - tasolla samaksi liberaalien ja konservatiivisten asenteiden ulottuvuudeksi. Toinen dimensio kuvaa tiukempaa samanmielisyyttä (S), kontrastina neutraali (?) ja maltillinen erimielisyys (s).

## 
## Principal inertias (eigenvalues):
## 
##  dim    value      %   cum%   scree plot               
##  1      0.037448  87.0  87.0  **********************   
##  2      0.003977   9.2  96.2  **                       
##  3      0.001041   2.4  98.6  *                        
##  4      0.000590   1.4 100.0                           
##         -------- -----                                 
##  Total: 0.043055 100.0                                 
## 
## 
## Rows:
##      name   mass  qlt  inr    k=1 cor ctr    k=2 cor ctr  
## 1  |   f1 |   60  990   36 | -125 614  25 |  -98 376 145 |
## 2  |   f2 |   83  997  163 | -289 983 185 |   35  14  25 |
## 3  |   f3 |   91  984   47 | -146 958  52 |   24  26  13 |
## 4  |   f4 |  101 1000   97 | -186 836  93 |   82 164 172 |
## 5  |   f5 |   98  879    4 |  -35 658   3 |   20 221  10 |
## 6  |   f6 |  100  951  176 |  256 866 175 |   80  85 162 |
## 7  |   m1 |   57  659   32 |   42  72   3 | -120 587 205 |
## 8  |   m2 |   66  977   57 | -187 946  62 |  -34  30  19 |
## 9  |   m3 |   78  457    5 |  -31 318   2 |  -20 139   8 |
## 10 |   m4 |   89  674   14 |   58 482   8 |  -37 192  30 |
## 11 |   m5 |   89  988   90 |  189 818  85 |  -86 170 166 |
## 12 |   m6 |   89  978  277 |  360 963 307 |   45  15  45 |
## 
## Columns:
##     name   mass  qlt  inr    k=1 cor ctr    k=2 cor ctr  
## 1 |    S |   99  915  128 |  196 695 102 |  110 220 304 |
## 2 |    s |  238  969  304 |  230 961 336 |   21   8  27 |
## 3 |      |  168  777   46 |   62 330  17 |  -73 447 223 |
## 4 |    e |  261  897   58 |  -68 473  32 |  -64 424 268 |
## 5 |    E |  234  997  464 | -286 962 513 |   55  35 177 |

Rivien massat ovat melko samankokoisia, mutta kolmen ryhmän (f2, f6 ja m6) osuus kokonaisinertiasta on 616 ja niiden kontribuutio ensimmäiselle dimensiolle on 567. Vain 36-45-vuotiaiden miesten (m3) piste on huonosti esitetty (qlt = 457). Tulkinta on hankalaa miesten ja naisten nuorimman ryhmän osalta, vaikka efekti kartalla on iso. Molempien osuus kokonaisinertiasta on pieni (inr). Nuoret naiset (f1) on kuvattu kartalla erittäin hyvin. Nuorten miesten (m1) esityksen laatu on heikompi, ja kaikista suurin kontribuutio on vain y-akselille. Kun muut ikäryhmät (paitsi f3) ovat ikäjärjestyksessä vasemmalta oikealle, voi nuorimpien ja vanhimpien ikäryhmien sijainnin tulkita osittain toisen dimension (varma mielipide - epävarma mielipide) avulla.

Selvästi kaikissa ikäluokissa miehet ovat konservatiivisempia kuin naiset. Nuorin ikäluokka on vähemmän varma mielipiteistään kuin vanhin. Yksi mahdollinen selitys kartan tulkinnan ongelmille on se, että maiden väliset erot mielipiteissä ovat paljon suurempia kuin sukupuolten väliset maiden sisällä (ISSP 1994 aineisto, CAiP, s.126).

5.2 Ikä, sukupuoli ja maa

Ikäluokan, sukupuolen ja maan yhteisvaikutusmuuttuja lisää kuvapisteiden määrää. Kuvasta 5.2 saa jotenkin selvää, kun sen suurentaa mutta pisteitä on selvästi liikaa. Joitain muuttujien nimiä voisi lyhentää, kuva-alaa voisi rajata joihinkin osiin mutta osajoukon korrespondenssianalyysi tarjoaa pätevimmän vaihtoehdon.

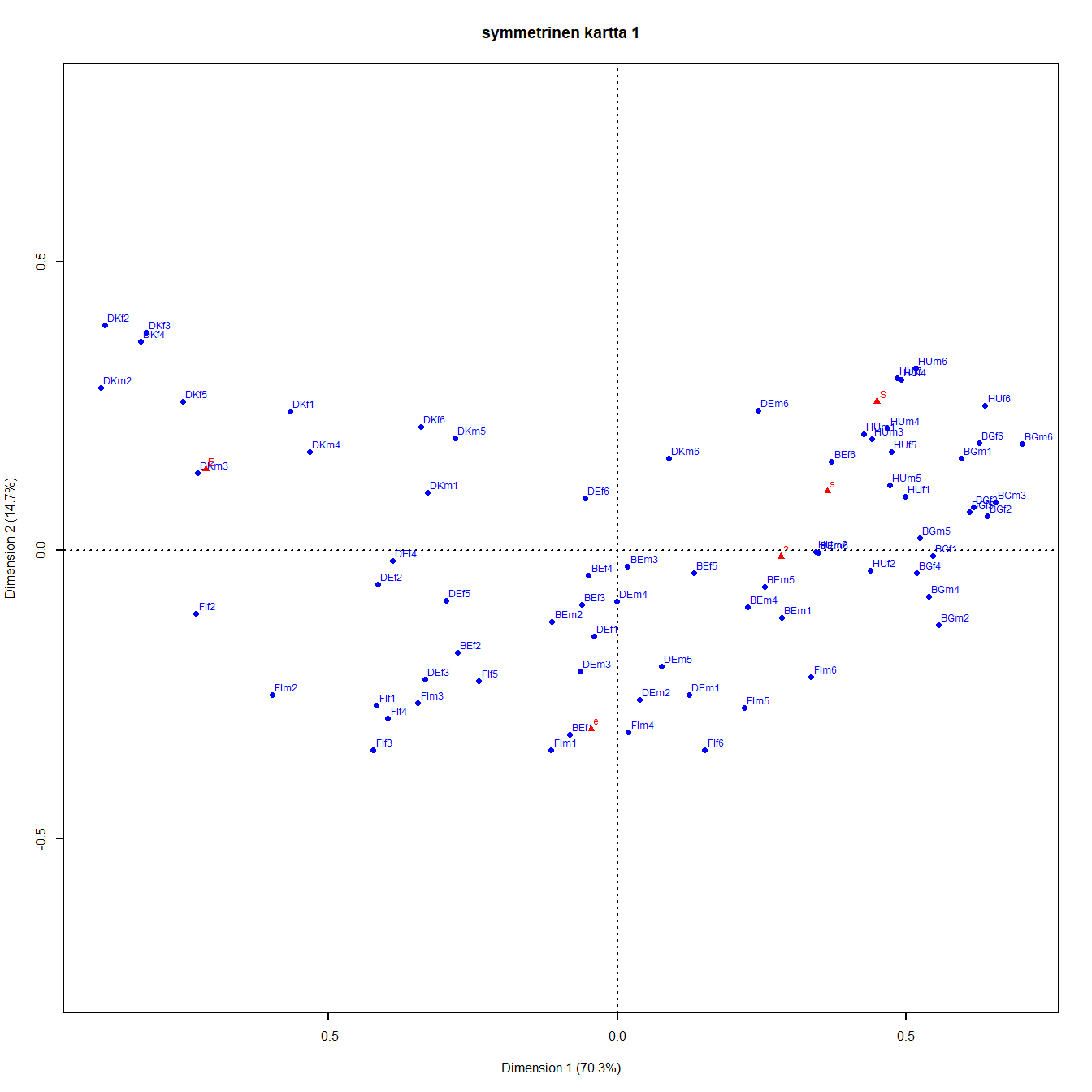
Kuva 5.2: Q1b: ikäluokka ja sukupuoli maittain

Sarakkeiden järjestys vasemmalta oikealle ja ylhäältä alas on sama kuin edellisissä kartoissa. Dimensioiden tulkinta on sama, osuus inertiasta pienenee x-akselilla noin 6 prosenttiyksikköä. Pisteiden järjestys liberaalista konservatiiviseen alkaa Tanskan ja Suomen pisteistä, sitten tulevat Saksan ja Belgian pisteet ja konservatiivisimpia ovat oikeassa laidassa Unkari ja Bulgaria. Toisella akselilla maltillisia ja neutraaleja ovat karkeasti Suomen pisteet ja lähes kaikki Saksan ja Belgian pisteet. Eri maiden osajoukkojen suhteita on hankalampi hahmottaa, erityisesti kartan oikealla laidalla.

Numeeristen tulosten taulukko on pitkä (ks. alle), mutta kartan informaatio pitää varmistaa. Numeeriset tulokset eivät ole pelkkää diagnostiikkaa ja kartan esittämien riippuvuuksien varmistamista. Niistä näkee myös tarkemmin mahdolliset kiinnostavat piirteet datassa. Regressiomallien tulosten raporteissa diagnostiikka on usein liitteenä, mutta eksploratiivisessa data-analyysissä se ohjaa analyysiä eteenpäin.

Tässä voi nähdä myös todennäköisyysteoriaan perustuvan tilastollisen mallintamisen vahvan puolen, aineiston rakenne ja muuttujien yhteydet saadaan parhaassa tapauksessa esitettyä paljon tiiviimmin.

## 
## Principal inertias (eigenvalues):
## 
##  dim    value      %   cum%   scree plot               
##  1      0.184895  70.3  70.3  ******************       
##  2      0.038751  14.7  85.0  ****                     
##  3      0.024006   9.1  94.1  **                       
##  4      0.015502   5.9 100.0  *                        
##         -------- -----                                 
##  Total: 0.263154 100.0                                 
## 
## 
## Rows:
##      name   mass  qlt  inr    k=1 cor ctr    k=2 cor ctr  
## 1  | BEf1 |   14  678    9 |  -83  43   1 | -320 635  38 |
## 2  | BEf2 |   24  914   11 | -278 650  10 | -177 264  20 |
## 3  | BEf3 |   21  320    3 |  -62  96   0 |  -95 224   5 |
## 4  | BEf4 |   24  164    3 |  -50  92   0 |  -44  71   1 |
## 5  | BEf5 |   23  332    5 |  133 304   2 |  -40  28   1 |
## 6  | BEf6 |   23  832   17 |  371 710  17 |  153 121  14 |
## 7  | BEm1 |   11  429    9 |  284 367   5 | -117  62   4 |
## 8  | BEm2 |   17  372    5 | -113 169   1 | -125 203   7 |
## 9  | BEm3 |   20  108    1 |   17  29   0 |  -29  79   0 |
## 10 | BEm4 |   22  966    5 |  225 812   6 |  -98 154   5 |
## 11 | BEm5 |   22  728    8 |  255 686   8 |  -63  42   2 |
## 12 | BEm6 |   26  788   15 |  348 788  17 |   -5   0   0 |
## 13 | BGf1 |    5  531   11 |  547 531   8 |   -9   0   0 |
## 14 | BGf2 |    8  860   14 |  640 853  17 |   59   7   1 |
## 15 | BGf3 |   12  815   21 |  617 804  24 |   75  12   2 |
## 16 | BGf4 |   10  932   12 |  519 927  15 |  -39   5   0 |
## 17 | BGf5 |   14  880   23 |  609 870  28 |   66  10   2 |
## 18 | BGf6 |   18  921   32 |  627 846  39 |  186  74  16 |
## 19 | BGm1 |    5  940    7 |  596 878   9 |  159  62   3 |
## 20 | BGm2 |    6  830    9 |  557 788  11 | -130  43   3 |
## 21 | BGm3 |    8  709   19 |  655 698  19 |   83  11   1 |
## 22 | BGm4 |    8  771   11 |  540 754  12 |  -81  17   1 |
## 23 | BGm5 |   10  979   11 |  524 977  15 |   21   2   0 |
## 24 | BGm6 |    9  692   27 |  701 647  24 |  184  45   8 |
## 25 | DEf1 |   13  425    3 |  -41  29   0 | -149 395   7 |
## 26 | DEf2 |   15  938   10 | -415 919  14 |  -60  19   1 |
## 27 | DEf3 |   19  846   13 | -333 582  11 | -224 264  24 |
## 28 | DEf4 |   23  985   13 | -390 982  19 |  -18   2   0 |
## 29 | DEf5 |   17  839    7 | -297 772   8 |  -87  67   3 |
## 30 | DEf6 |   23  116    8 |  -56  32   0 |   90  84   5 |
## 31 | DEm1 |   13  912    4 |  124 180   1 | -250 732  20 |
## 32 | DEm2 |   13  766    4 |   38  16   0 | -259 749  22 |
## 33 | DEm3 |   15  737    4 |  -64  63   0 | -210 674  17 |
## 34 | DEm4 |   21  137    5 |   -1   0   0 |  -89 137   4 |
## 35 | DEm5 |   19  603    5 |   76  75   1 | -202 529  20 |
## 36 | DEm6 |   22  849   12 |  244 427   7 |  242 422  34 |
## 37 | DKf1 |   10  991   15 | -567 839  18 |  241 152  15 |
## 38 | DKf2 |   14  991   49 | -888 831  58 |  389 160  53 |
## 39 | DKf3 |   17  963   53 | -816 793  60 |  377 170  61 |
## 40 | DKf4 |   18  977   57 | -826 820  66 |  362 157  61 |
## 41 | DKf5 |   16  998   38 | -753 894  48 |  258 105  27 |
## 42 | DKf6 |   12  808    9 | -340 579   8 |  214 229  14 |
## 43 | DKm1 |   15  981    7 | -329 898   9 |  100  83   4 |
## 44 | DKm2 |   13  989   43 | -895 900  55 |  282  89  26 |
## 45 | DKm3 |   13  982   28 | -728 950  38 |  134  32   6 |
## 46 | DKm4 |   15  941   19 | -534 855  24 |  170  86  11 |
## 47 | DKm5 |   13  643    9 | -281 435   6 |  194 208  13 |
## 48 | DKm6 |   15  355    5 |   89  85   1 |  158 270   9 |
## 49 | FIf1 |   12  980   11 | -417 693  11 | -269 287  21 |
## 50 | FIf2 |   12  927   26 | -730 907  34 | -110  21   4 |
## 51 | FIf3 |   12  984   13 | -423 590  11 | -346 394  36 |
## 52 | FIf4 |   14  991   14 | -398 644  12 | -292 347  32 |
## 53 | FIf5 |   17  952    8 | -240 502   5 | -227 450  23 |
## 54 | FIf6 |   11  835    7 |  151 134   1 | -347 701  35 |
## 55 | FIm1 |    7  787    5 | -115  78   1 | -347 710  22 |
## 56 | FIm2 |    9  977   14 | -598 832  17 | -250 146  14 |
## 57 | FIm3 |    9  998    6 | -345 629   6 | -265 369  16 |
## 58 | FIm4 |   13  837    6 |   19   3   0 | -316 834  33 |
## 59 | FIm5 |   12  734    7 |  220 289   3 | -273 446  23 |
## 60 | FIm6 |    9  911    6 |  336 637   6 | -220 274  12 |
## 61 | HUf1 |    7  723    9 |  499 698   9 |   93  25   1 |
## 62 | HUf2 |   11  689   11 |  438 685  11 |  -35   4   0 |
## 63 | HUf3 |   12  808   18 |  484 586  15 |  298 222  27 |
## 64 | HUf4 |   11  768   18 |  491 564  15 |  296 204  25 |
## 65 | HUf5 |   12  850   13 |  474 753  14 |  170  97   9 |
## 66 | HUf6 |   13  671   34 |  637 581  28 |  251  90  21 |
## 67 | HUm1 |    6  935    5 |  426 766   6 |  201 170   6 |
## 68 | HUm2 |    9  381   11 |  344 381   6 |   -2   0   0 |
## 69 | HUm3 |   13  957   12 |  441 803  13 |  193 154  12 |
## 70 | HUm4 |   10  999   10 |  468 830  12 |  211 169  11 |
## 71 | HUm5 |   13  942   12 |  472 891  15 |  113  51   4 |
## 72 | HUm6 |    8  726   15 |  517 529  11 |  315 197  20 |
## 
## Columns:
##     name   mass  qlt  inr    k=1 cor ctr    k=2 cor ctr  
## 1 |    S |   99  653  155 |  450 492 109 |  258 162 171 |
## 2 |    s |  238  741  174 |  364 687 170 |  102  54  63 |
## 3 |      |  168  535   96 |  284 534  73 |  -11   1   1 |
## 4 |    e |  261  941  103 |  -45  20   3 | -310 921 646 |
## 5 |    E |  234 1000  471 | -714 962 645 |  141  37 119 |

Tuloksista nähdään, että sarakkeet on kohtalaisen hyvin esitetty, heikoimmin neutraali vaihtoehto (qlt = 535). Kun sen suhteellinen kontribuutio (cor) on vain 1 toisella dimensiolla jää loppuosa x-akselille. Maltillisuuden dimensiota määrittää e-sarake (ctr = 646), ja vain sitä. Ensimmäistä dimensiota määrittää vahvimmin E-sarake (ctr = 645) liberaaliin ja samaa mieltä olevien sarakkeet (s, S) konservatiiviseen suuntaan.

Kun aineistossa on 72 riviä, on inertian suhteellisen kontribuution keskiarvo noin 14. Tämän ylittäviä kontribuutiota on Bulgarian naisilla (BGf2, BGf3, BGf5 ja BGf6), kaikilla konservatiiviseen suuntaan. Sama pätee Unkarin naisille, muuten naisten ikäluokat kontribuoivat yleensä liberaaliin suuntaan. Suomen pisteiden absoluuttiset kontribuutiot ovat lähes pelkästään toiselle dimensiolle maltilliseen suuntaan. Tanska taas kontribuoi vahvasti jyrkempien mielipiteiden suuntaan.

5.3 Stabiilisuus

Tarkastelen tässä vain ratkaisustabiiliutta (solution stability). Siinä data on annettu, ja ratkaisun numeerisista tuloksista nähdään miten pisteet määrittävät akselit. Ratkaisu on stabiili niiden pisteiden suhteen, jotka eivät vaikuta siihen.

Ulkoinen stabiilius on laajempi käsite, siinä huomioidaan esimerkiksi datan suhde johonkin perusjoukkoon (CAiP, s. 225).

Korrespondenssianalyysiä ja erityisesti khii2- etäisyysmittaa on arvosteltu siitä, että se on liian herkkä harvinaisille luokittelumuuttujan arvoille. Yhteenvetoartikkelissaan M. Greenacre (2006) tarttuu ”vaikuttavien poikkeavien havaintojen myyttiin”, ja pitää sitä lähes aina perusteettomana.

Harvinaiset kategoriat ovat usein kartalla kaukana origosta, mutta jokaisella pisteellä on massa ja näillä poikkeavilla havainnoilla (outlier) se on pieni. Niinpä niiden vaikutuskin on vaatimaton.

Harvinaisten kategorioiden vaikutus voi olla suuri, joten numeerisista tuloksista on tarkistettava, onko hyvin pienen massan pisteillä suuri kontribuutio ratkaisuun. Käytännössä näin voi käydä esimerkiksi silloin, kun jonkun harvinaisen luokittelumuuttujan arvon havainnot ovat keskittyneet muutamaan profiiliin, joissa niiden osuus on suuri (CAiP, s 298). Luvussa 7 nähdään, miten melko vähäinen määrä puuttuvia vastauksia kasaantuu samaan vastaajien osajoukkoon ja mitä seurauksia sillä on.

Stabiiliutta voi helposti kokeilla määrittelemällä joitain pisteitä täydentäviksi pisteiksi.

En löytänyt kartan 5.2 numeerisista tuloksista pienen massan pisteitä, joilla on merkittävä kontribuutio akseleihin.

Luku 6 Osajoukon korrespondenssianalyysi

Graafisessa data-analyysissä kuvien on oltava selkeitä, mutta korrespondenssianalyysin kartat ovat usein liian täynnä pisteitä. Ongelmaa voi lieventää jättämällä pois ratkaisuun vain vähän vaikuttavia pisteitä, keksimällä mahdollisimman lyhyitä symboleja muuttujille tai rajaamalla kuvaa. Ongelma on kuitenkin syvempi, usein kartta kertoo aika yllätyksettömän ja ilmeisen tarinan. Kiinnostavammat yhteydet pysyvät piilossa ylemmissä dimensioissa. MCA-kartan perusongelma on se, että siinä yritetään esittää monia erityyppisiä yhteyksiä simultaanisesti ja nämä yhteydet eivät ole “isolated to particular dimensions” (Greenacre ja Pardo artikkelikokoelmassa (M. Greenacre ja Blasius 2006), s. 198).

Osajoukon korrespondenssianalyysi (subset CA, subset MCA) on yksi vastaus tähän pulmaan. Teoreettiset perusteet on esitetty Greenacren ja Pardon artikkelissa (M. Greenacre ja Pardo 2006). Artikkelin laajennetussa versiossa (emt.) esimerkkiaineistona on ISSP:n 1994 data. Selkeä oppikirjaesitys on CAiP (ss. 161-).

Eräs sovelluskohde yhteiskuntatieteellisissä kyselyaineistoissa on puuttuvien vastausten analyysi, johon palataan seuraavassa luvussa.

Osajoukon korrespondenssianlyysin idea on säilyttää koko aineiston massat ja khii2-etäisyyksien painot mutta analysoida vain osaa aineistosta. Koko aineiston sentroidi säilyy kartan keskipisteenä. Osajoukkojen inertioiden summa on koko aineiston inertia.

Osajoukon voi valita havaintojen tai muuttujien suhteen. Täydentäviä pisteitä voi helposti lisätä kartalle, jos ne eivät kuulu siihen joukkoon, josta osajoukko on valittu. Osajoukon profiilit muuttuvat, niiden summa ei enää ole yksi ja barysentristä periaatetta ei voi suoraan käyttää täydentävän pisteen koordinaattien laskemiseen. Tässä esimerkissä emme voi suoraan ca-paketin avulla sijoittaa esimerkiksi maapisteitä kartoille.

Kartan 5.2 avulla aineiston voi jakaa kahteen ryhmään. Suomi, Tanska ja Saksa ovat pääakselin oikealla puolella. Bulgaria ja Unkari ja Belgian kanssa ovat toinen ryhmä.

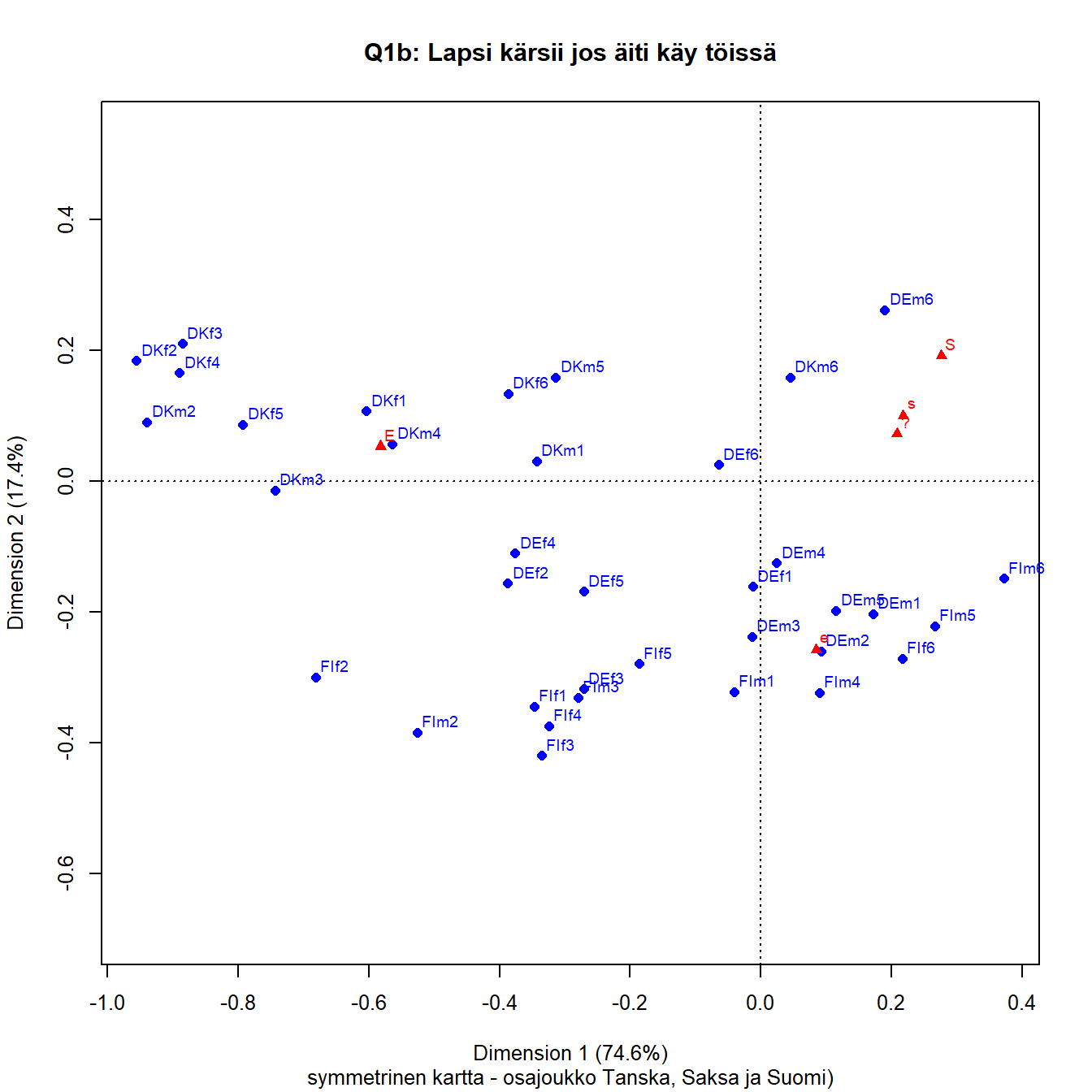
Kuva 6.1: Ikä, sukupuoli ja maa:Tanska-Saksa-Suomi

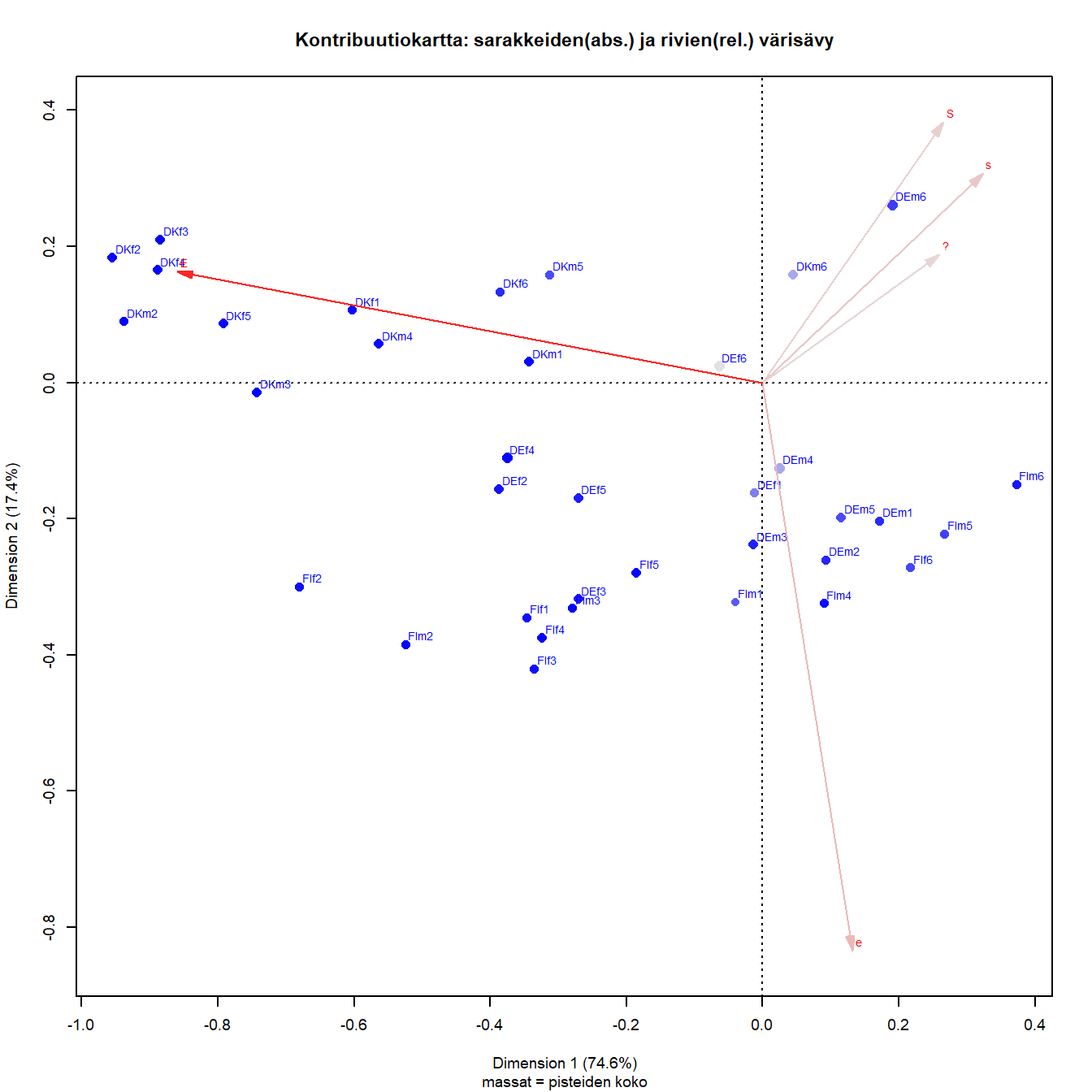
Kuva 6.2: Ikä, sukupuoli ja maa:Tanska-Saksa-Suomi

Karttoja 6.1 ja 6.2 joutuu katsomaan aika tarkkaan ennen kuin uskoo, että akseleiden skaalaus on akateeminen pulma vailla käytännön merkitystä (kts. luku 3.4). Dataa analysoidaan graafisesti, ja kuvat näyttävät erilaisilta. Pääakselien inertioiden neliöjuuret eivät poikkea toisistaan huomattavasti (0.327 ja 0.158), joten sarakkeiden etäisyyksiä voisi tulkita myös kontribuutiokuvista.

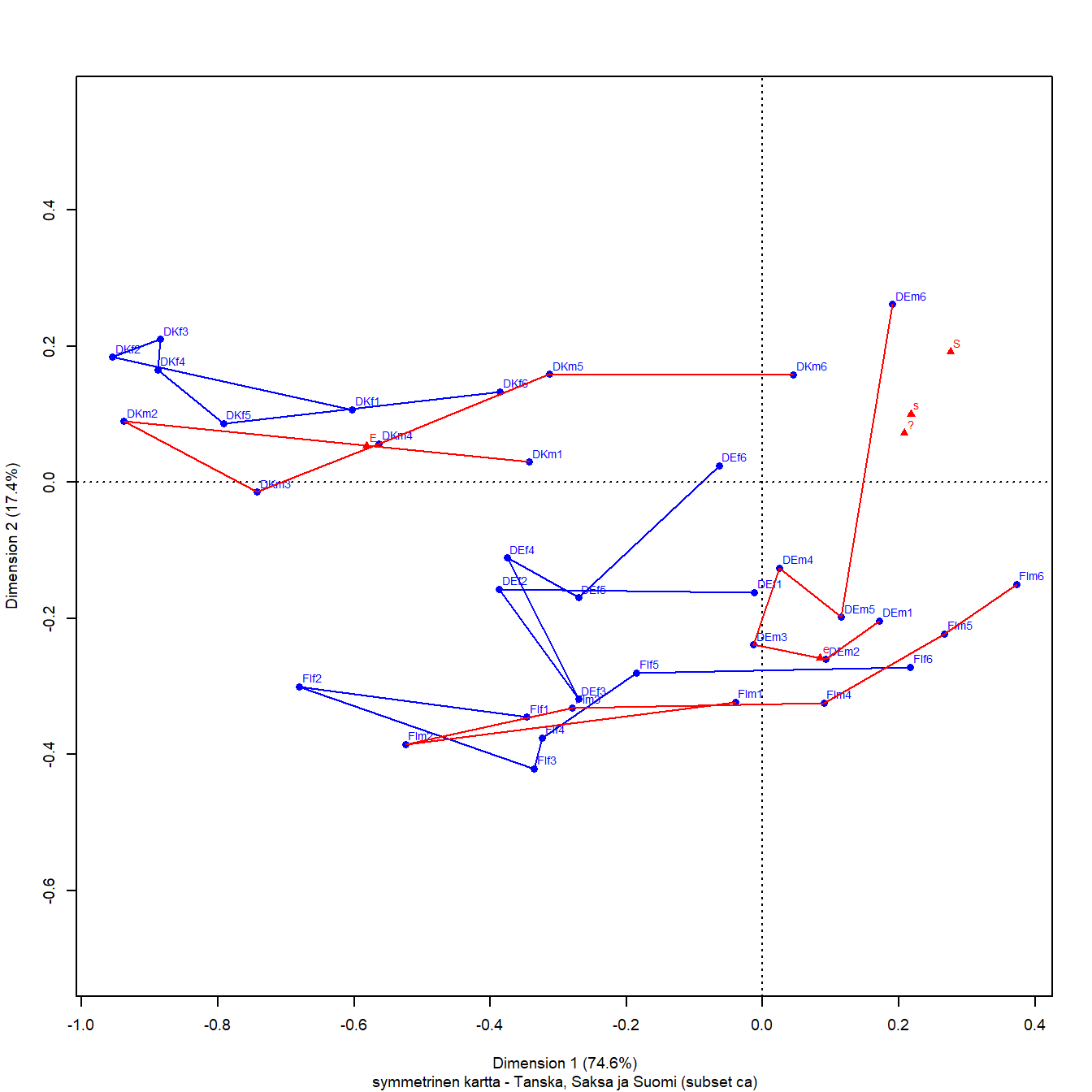
Kuva 6.3: Ikä, sukupuoli ja maa:Tanska-Saksa-Suomi

## 
## Principal inertias (eigenvalues):
## 
##  dim    value      %   cum%   scree plot               
##  1      0.107090  74.6  74.6  *******************      
##  2      0.024985  17.4  92.0  ****                     
##  3      0.006594   4.6  96.6  *                        
##  4      0.004882   3.4 100.0  *                        
##         -------- -----                                 
##  Total: 0.143551 100.0                                 
## 
## 
## Rows:
##      name   mass  qlt  inr    k=1 cor ctr    k=2 cor ctr  
## 1  | DEf1 |   13  467    5 |  -12   3   0 | -162 464  13 |
## 2  | DEf2 |   15  930   19 | -387 799  21 | -157 131  14 |
## 3  | DEf3 |   19  919   25 | -271 385  13 | -318 533  76 |
## 4  | DEf4 |   23  993   25 | -376 913  30 | -111  80  11 |
## 5  | DEf5 |   17  893   13 | -271 641  11 | -169 252  19 |
## 6  | DEf6 |   23   48   15 |  -64  42   1 |   24   6   1 |
## 7  | DEm1 |   13  827    8 |  172 345   3 | -203 482  21 |
## 8  | DEm2 |   13  855    8 |   93  96   1 | -260 759  34 |
## 9  | DEm3 |   15  874    7 |  -13   3   0 | -238 871  34 |
## 10 | DEm4 |   21  285    8 |   25  11   0 | -126 274  13 |
## 11 | DEm5 |   19  684   10 |  116 174   2 | -198 510  30 |
## 12 | DEm6 |   22  750   22 |  190 260   8 |  261 490  61 |
## 13 | DKf1 |   10  979   27 | -603 949  35 |  107  30   5 |
## 14 | DKf2 |   14  996   89 | -955 960 115 |  184  36  18 |
## 15 | DKf3 |   17  985   98 | -885 933 122 |  210  53  29 |
## 16 | DKf4 |   18  983  104 | -889 950 132 |  165  33  20 |
## 17 | DKf5 |   16 1000   69 | -792 988  92 |   86  12   5 |
## 18 | DKf6 |   12  834   17 | -386 745  17 |  133  89   9 |
## 19 | DKm1 |   15  978   13 | -342 971  17 |   30   7   1 |
## 20 | DKm2 |   13  997   79 | -938 988 104 |   90   9   4 |
## 21 | DKm3 |   13  989   52 | -743 989  69 |  -14   0   0 |
## 22 | DKm4 |   15  962   36 | -563 952  45 |   57  10   2 |
## 23 | DKm5 |   13  682   16 | -314 543  12 |  159 139  13 |
## 24 | DKm6 |   15  291    9 |   45  22   0 |  158 269  15 |
## 25 | FIf1 |   12  951   20 | -346 478  13 | -345 474  55 |
## 26 | FIf2 |   12  941   48 | -680 788  50 | -300 153  42 |
## 27 | FIf3 |   12  952   24 | -335 370  12 | -420 582  82 |
## 28 | FIf4 |   14  999   25 | -323 426  14 | -375 573  82 |
## 29 | FIf5 |   17  982   14 | -185 299   6 | -280 683  55 |
## 30 | FIf6 |   11  704   13 |  217 274   5 | -271 430  33 |
## 31 | FIm1 |    7  624    8 |  -40  10   0 | -323 614  30 |
## 32 | FIm2 |    9  984   26 | -525 640  22 | -385 344  52 |
## 33 | FIm3 |    9  990   12 | -279 412   6 | -331 578  38 |
## 34 | FIm4 |   13  944   11 |   90  67   1 | -324 877  54 |
## 35 | FIm5 |   12  722   14 |  267 426   8 | -222 295  23 |
## 36 | FIm6 |    9  911   11 |  373 785  12 | -150 126   8 |
## 
## Columns:
##     name   mass  qlt  inr    k=1 cor ctr    k=2 cor ctr  
## 1 |    S |   99  731  107 |  276 493  71 |  192 238 147 |
## 2 |    s |  238  832  114 |  218 688 105 |  100 144  94 |
## 3 |      |  168  647   88 |  208 576  68 |   73  70  35 |
## 4 |    e |  261  992  135 |   85  96  17 | -258 896 697 |
## 5 |    E |  234 1000  556 | -582 992 739 |   53   8  27 |

Tulkintaa

Kolmen maan osajoukon ratkaisussa 2. dimensiolla (maltillinen liberaali - tiukka konservatiivi) on inertiasta 17 prosenttia, edellä ollut paljon yksiulotteisempia ratkaisuja. Huono kvaliteetti (qlt) on ryhmillä DEf1 (467) ja DEf6 (48), DEm4 (285). Tanskan havainnoista vanhimmat miehet (DKm6,291) ovat kaikkein huonoimmin esitettyjä ratkaisussa, ja hieman nuoremmatkin (DKm5, 682). Suomen aineistossa vain nuoret miehet (FIm1, 624) on esitetty kartalla huonosti. Kaksi dimensiot selittävät osajoukon kokonaishajonnasta 92 prosenttia, mutta muutaman ryhmän hajonta on muissa dimensioissa. Saksan naisten iäkkäin ikäluokka (DEf6) ja keski-ikäisen miehet (DEm4) vain näyttävät olevan lähekkäin origon tuntumassa, samoin muutama muu huonosti tasoon sijoitettu piste. Huonosti kuvatuista pisteistä kuva ei oikeastaan mitään muuta.

Sarakkeet on esitetty kohtalaisen hyvin, ja symmetrisessä kartassa tärkeimmälle dimensioille projisoidut sarakepisteet ovat odotetussa järjestyksessä.

Kontribuutiokartasta nähdään, että tärkein kontrasti on tiukan erimielisyyden (E) ja kaikkien muiden vastausvaihtoehtojen välillä. Epävarmojen tai maltillisten (e) kontrasti hallitsee toista dimensiota, erityisesti S- ja s- kategorioiden kanssa. Samalla kuvasta näkee (ja numeerisista tuloksista voi vahvistaa), että S-piste on on lähempänä (kulma on pienempi) pystyakselia. Kontribuutio on suurempi (147 vs. 71 x-akselille). Toisaalta x-akseli selittää selvästi suurimman osan kaikkien muiden sarakepisteiden inertiasta, ja y-akseli taas lähes täysin e-pisteen inertian.

Kartasta 6.3 nähdään, että naisten ikäluokat ovat kaikissa maissa liberaalimpia kuin vastaavat miesten ikäluokat. Nuorin ikäluokka on konservatiivisemmalla puolella ja samalla toisella dimensiolla maltillisemmalla puolella. Vanhemmat ikäluokat ovat konservatiivisempia.

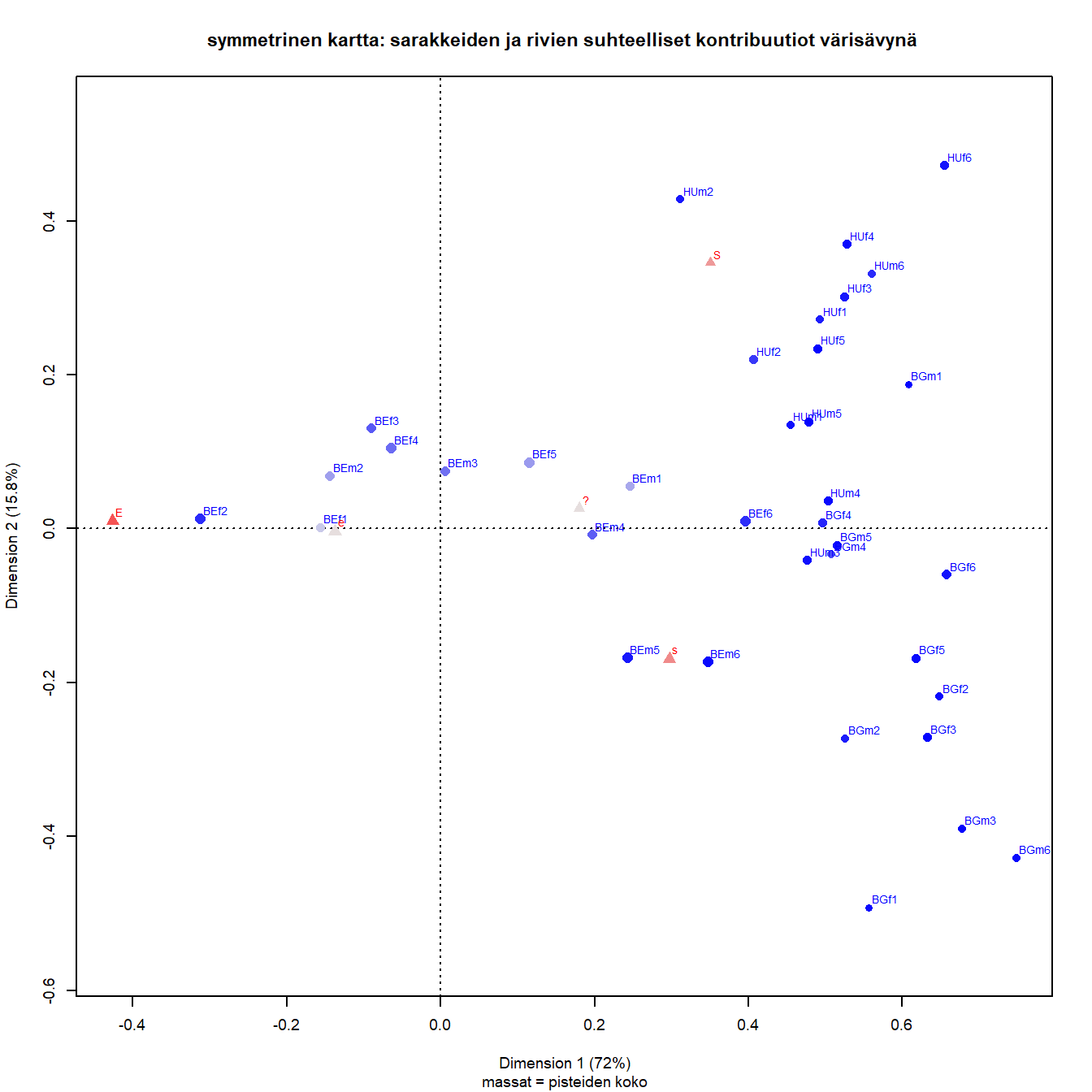
Kuva 6.4: Ikä, sukupuoli ja maa: Belgia-Bulgaria - Unkari

Belgian, Unkarin ja Bulgarian kartalla ensimmäisen dimension tulkinta pysyy samana, mutta nyt molemmat erimieliset (E, e) vastauskategoriat ovat selvästi vasemmalla liberaalilla puolella. Ne ovat lähes x-akselin päällä, kun ensimmäisen osajoukon kartalla e-sarake oli oikealla ja alhaalla kontrastina S- ja s- vastauksille ja myös neutraalille vaihtoehdolle. Kartan toinen dimensio erottelee nyt tiukasti ja lievemmin samaa mieltä olevat, neutraali vaihtoehto jää väliin.

Belgian nuoremmat ikäluokat ovat liberaalilla puolella, ja kiinnostavasti kaksi vanhinta miesten ryhmää on pystysuunnassa kaikkein maltillisimpia. Bulgarian ja Unkarin pisteen ovat tiukasti konservatiivisella puolella. Vaihtelua on maltillisemman ja jyrkemmän konservatiivisuuden välillä pystysuuntaan. Toisen dimension kontrasti on myös hieman yllättäen Bulgarian nuorimpien naisten (BGf1) Unkarin vanhimpien naisten (HUf6) välillä.

Kuvan 6.3 tapaan ei Bulgarian ja Unkarin ikäluokkia kannata yhdistää. Järjestys toki löytyy, mutta ei ollenkaan niin selkeä. Saksan naisten ikäluokkakuva alkaa erkaantua hieman Suomen ja Tanskan hyvin samanlaisista kuvioista. Saksan miehillä on jo eroja paljon toisen dimension suuntaan, Unkarin ja Bulgarian osajoukkojen erot ovat lähes pelkästään pystysuoria.

Suhteellinen kontribuutio eli pisteen laatu (numeerisissa tuloksissa “cor”) on esitetty värisävynä. Sarakkeista e ja “?” on esitetty huonosti, riveistä Belgian nuorimmat miehet ja naiset.

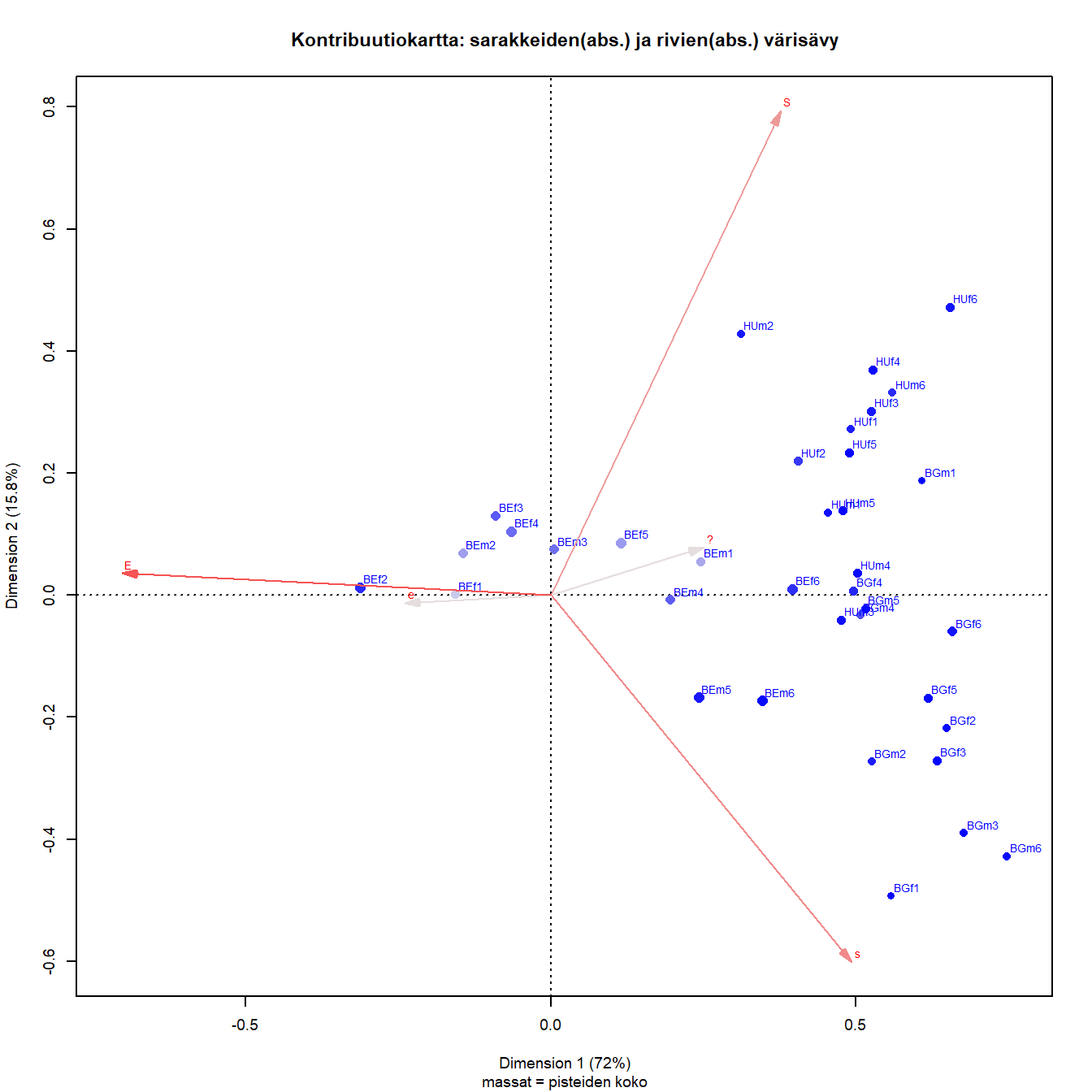
Kuva 6.5: Ikä, sukupuoli ja maa: Belgia-Bulgaria - Unkari 2

Kontribuutiokartta 6.5 eroaa kartasta 6.2 kolmen akselin (E, S ja s) erilaisella vaikutuksella ratkaisuun. Konservatiiviset sarakepisteet ovat vaikuttavampia kuin E, maltillinen liberaali (s) ja neutraali vaihtoehto vaikuttavat vähemmän.

Listataan vielä toisen osajoukon ratkaisun numeeriset tulokset.

## 
## Principal inertias (eigenvalues):
## 
##  dim    value      %   cum%   scree plot               
##  1      0.086111  72.0  72.0  ******************       
##  2      0.018841  15.8  87.8  ****                     
##  3      0.011172   9.3  97.1  **                       
##  4      0.003477   2.9 100.0  *                        
##         -------- -----                                 
##  Total: 0.119602 100.0                                 
## 
## 
## Rows:
##      name   mass  qlt  inr    k=1 cor ctr    k=2 cor ctr  
## 1  | BEf1 |   14  152   19 | -156 152   4 |    2   0   0 |
## 2  | BEf2 |   24  826   24 | -313 824  28 |   13   1   0 |
## 3  | BEf3 |   21  623    7 |  -90 201   2 |  130 422  19 |
## 4  | BEf4 |   24  556    6 |  -65 155   1 |  105 401  14 |
## 5  | BEf5 |   23  355   11 |  115 227   3 |   86 128   9 |
## 6  | BEf6 |   23  810   37 |  396 810  41 |   10   0   0 |
## 7  | BEm1 |   11  288   21 |  246 274   8 |   55  14   2 |
## 8  | BEm2 |   17  333   11 | -144 271   4 |   68  61   4 |
## 9  | BEm3 |   20  531    2 |    6   4   0 |   75 528   6 |
## 10 | BEm4 |   22  620   11 |  197 618  10 |   -8   1   0 |
## 11 | BEm5 |   22  917   18 |  243 620  15 | -168 297  33 |
## 12 | BEm6 |   26  977   33 |  347 782  36 | -173 195  41 |
## 13 | BGf1 |    5  979   23 |  557 549  18 | -492 430  63 |
## 14 | BGf2 |    8  974   32 |  649 875  38 | -219  99  20 |
## 15 | BGf3 |   12 1000   46 |  633 844  54 | -271 155  45 |
## 16 | BGf4 |   10  847   25 |  496 847  30 |    7   0   0 |
## 17 | BGf5 |   14  961   50 |  618 894  62 | -168  66  21 |
## 18 | BGf6 |   18  939   71 |  658 931  92 |  -60   8   4 |
## 19 | BGm1 |    5  999   15 |  608 912  19 |  188  87   9 |
## 20 | BGm2 |    6  892   21 |  526 703  20 | -273 189  25 |
## 21 | BGm3 |    8  994   41 |  677 746  43 | -390 247  64 |
## 22 | BGm4 |    8  669   25 |  508 666  23 |  -34   3   0 |
## 23 | BGm5 |   10  949   24 |  516 947  32 |  -22   2   0 |
## 24 | BGm6 |    9  978   58 |  748 737  60 | -428 241  89 |
## 25 | HUf1 |    7  888   20 |  493 681  19 |  271 207  26 |
## 26 | HUf2 |   11  762   25 |  406 589  20 |  220 173  27 |
## 27 | HUf3 |   12  916   39 |  525 688  37 |  301 227  56 |
## 28 | HUf4 |   11  970   40 |  528 651  36 |  370 319  81 |
## 29 | HUf5 |   12  985   29 |  490 802  32 |  234 183  34 |
## 30 | HUf6 |   13  933   75 |  655 614  64 |  472 319 151 |
## 31 | HUm1 |    6  948   12 |  455 871  14 |  135  77   6 |
## 32 | HUm2 |    9  902   24 |  312 313  10 |  428 589  90 |
## 33 | HUm3 |   13  945   26 |  477 938  33 |  -41   7   1 |
## 34 | HUm4 |   10  965   22 |  503 960  29 |   36   5   1 |
## 35 | HUm5 |   13  993   26 |  478 916  33 |  139  77  13 |
## 36 | HUm6 |    8  839   33 |  560 622  29 |  331 217  46 |
## 
## Columns:
##     name   mass  qlt  inr    k=1 cor ctr    k=2 cor ctr  
## 1 |    S |   99  944  214 |  351 479 142 |  346 465 630 |
## 2 |    s |  238  942  247 |  297 711 244 | -169 231 362 |
## 3 |      |  168  435  107 |  180 426  63 |   26   9   6 |
## 4 |    e |  261  640   65 | -138 639  57 |   -4   0   0 |
## 5 |    E |  234  966  368 | -426 965 494 |   10   1   1 |

Kahden osajoukon inertioiden summa on sama kuin koko aineiston (0.144 + 0.12 = 0.263). Selitysasteet nousevat hieman, ja aineiston riippuvuuden rakenteesta saadaan esiin selviä eroja. Osajoukkojen analyysi täydentää ja tarkentaa yleiskuvaa (ks. Kuva 5.2).

Belgian pisteistä osalla on huono kvaliteetti (BEf1, BEf5, BEm1, BEm2). Bulgaria ja Unkari hyvin esitetty. Belgia on pulmallinen tapaus, ehkä taas omissa dimensioissaan. Belgian poikkeavuus (annetulla aluejaolla) on kiinnostava havainto, korrespondenssianalyysin tavoite ei ole pelkästään kohtuullisen luotettava yleiskuva taulukon riippuvuuksista. Poikkeavat havainnot eivät ole ongelma, vaan datan ominaisuus.

Luku 7 Monimuuttujakorrespondenssianalyysi (MCA)

Usean muuttujan samanaikainen analyysi voidaan korrespondenssianalyysissä jakaa kahteen erilaiseen tutkimusasetelmaan. Ensimmäisessä tutkitaan kahden erilaisen muuttujaryhmän välisiä suhteita, toisessa yhden homogeenisen muuttujaryhmän sisäisiä suhteita.

Esimerkkiaineistossa haastateltavien vastaukset substanssikysymyksiin ovat oma ryhmänsä ja taustamuuttujat toinen ryhmä. Kahden muuttujaryhmän välisiä suhteita voidaan tutkia rakentamalla yhdistetty matriisi useasta kahden muuttujan ristiintaulukoinnista. Tämä pinottujen ja yhdistettyjen (stacked and concatenated) taulukoiden menetelmä (CAiP s. 129) ei kerro muuttujaryhmien sisäisistä yhteyksistä, joita edellä analysoitiin vuorovaikutusmuuttujien avulla.

Toinen asetelma on keskenään homogeenisten muuttujien välisten suhteiden analyysi. Monimuuttujakorrespondenssianalyysi (multiple correspondence analysis, MCA) soveltuu hyvin kyselytutkimusten vastausten analyysiin. MCA - kartoilla voidaan esittää myös havainnot, mutta usein on järkevämpää käyttää kartalla taustamuuttujien keskiarvopisteitä. Keskiarvopisteisiin voi simuloimalla lisätä luottamusellipsit (CAiP, s. 299).

Esitän molemmista analyyseistä yhden esimerkin. MCA-esimerkissä otan käyttöön kaikki aineiston havainnot ja useita vastausmuuttujia, puuttuvat tiedot ovat mukana yhtenä luokittelumuuttujan arvona.

Yksinkertaisen korrespondenssianalyysin yleistys usean muuttujan samanaikaiseen analyysiin ei ole aivan yksikertainen asia. Geometrinen tulkinta ei ole läheskään niin selkeä kuin yksinkertaisessa korrespondenssianalyysissä. Silti MCA toimii käytännössä usein hyvin juuri kyselytutkimusten analyysissä. MCA-kartat esittävät luokittelumuuttujien arvot kartalla optimaalisesti. Jokainen rivipiste (havainto) sijoittuu kartalle valitsemiensa vastausvaihtoehtojen keskiarvopisteeseen. MCA-kartalla nämä luokittelumuuttujien arvoja vastaavat sarakepisteet maksimoivat rivipisteiden hajonnan kartalla (Greenacre ja Hastie 1987 , s. 444-445).

7.1 Pinotut ja yhdistetyt taulukot

Pinottujen taulukoiden idea on esitetty kuvassa 7.1. Taulukossa kaksi “selitettävää” muuttujaa on ristiintaulukoitu kolmen taustamuuttujan kanssa.

Jos reunajakaumat ovat samat eli puuttuvia tietoja ei ole, taulukon kokonaisinertia on osataulukoiden inertioiden keskiarvo. Taulukon analyysi on yhden kysymyksen ja yhden taustamuuttujan parittaisten suhteiden analyysiä, yksi pari kerrallaan.

Pierre Bourdieun tunnettu tutkimus La Distiction (1979) sovelsi tätä menetelmää. Ranskan väestö luokitellaan ammattiryhmiin ja taulukoidaan useiden elämäntapaa kuvaavien muuttujien kanssa. Taulukot yhdistetään pinoamalla ne päällekkäin (M. Greenacre ja Blasius (2006) , s.21).

Kuva 7.1: Pinotut ja yhdistetyt taulut - periaate

Seuraavassa esimerkissä “selitettäviä” luokittelumuuttujia on vain yksi. Tällainen pinotun taulun analyysi on eräänlainen kaikkien siihen kuuluvien taulukoiden “keskiarvokartta” (CAiP, s 136). Kysymyksen Q1b vastausten ristiintaulukointi ikäluokan ja sukupuolen kanssa liitetään maarivien taulukkoon.

Pisteiden määrä kartoilla kasvaa, ja muuttujanimiä joudutaan tiivistämään. Toinen tekninen detalji on kartan kääntäminen. Kuvat kääntyvät herkästi akselien ympäri, vertailun helpottamiseksi koordinaattien etumerkkejä joutuu joskus muuttamaan (kts. Liite 3: R-koodi).

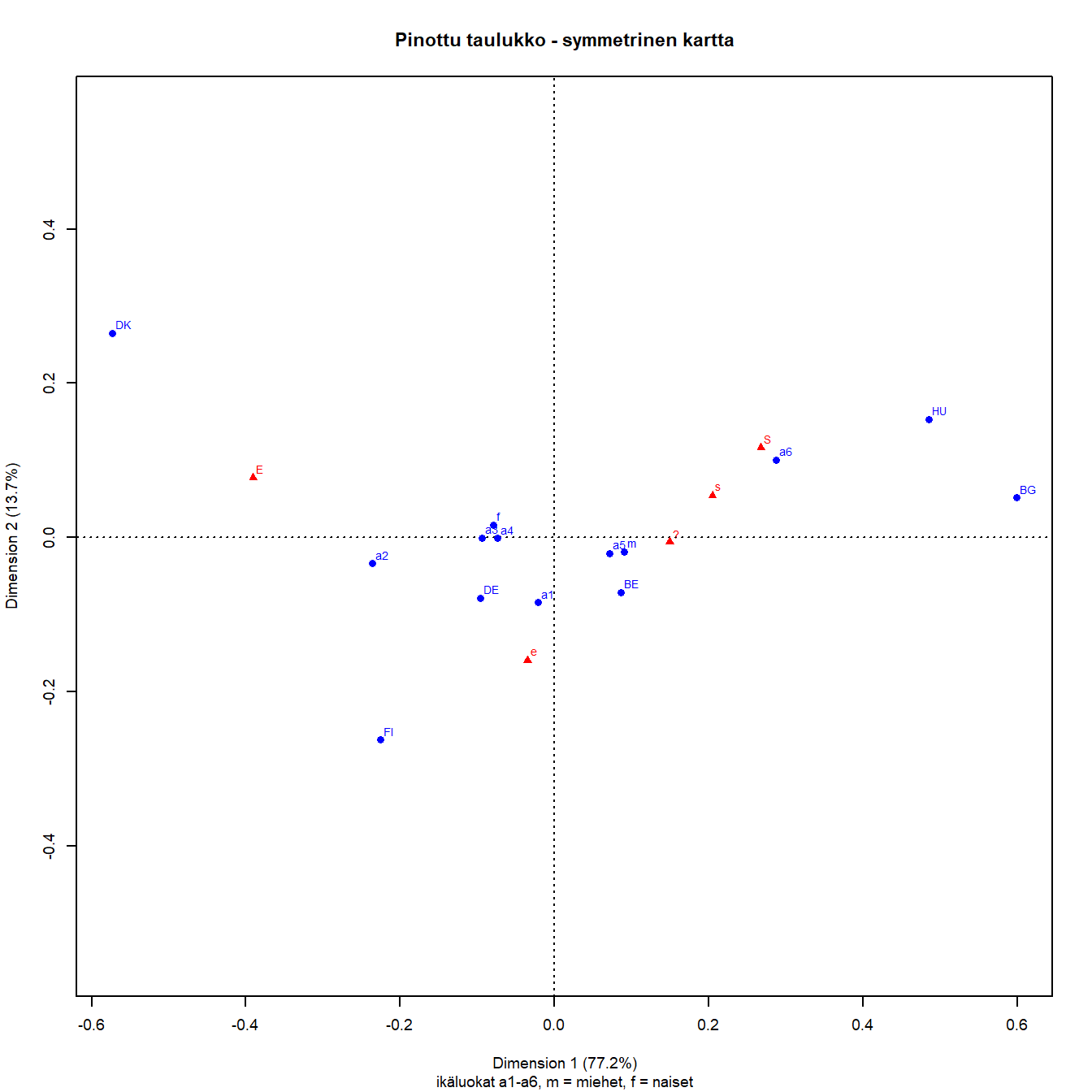
Kuva 7.2: Q1b: Lapsi kärsii jos äiti käy työssä

Kuvassa 7.2 on esitetty pinotun taulukon kartta. Tulkinta ei muutu, eikä maapisteiden sijaintikaan.

Koko aineiston kartassa ikäluokkapisteet ja sukupuolipisteet ovat pakkautuneet maapisteitä tiiviimmin origon ympärille. Ikäluokkapisteiden (koko aineiston keskiarvot) selvä kontrasti on vanhimman (a6) ja toiseksi nuorimman välillä 1. dimension suuntaan.

Ikäluokkapisteet ovat koko aineiston keskiarvopisteitä, niiden sijaintia voi tulkita pistejoukko kerrallaan kuten maapisteidenkin. Naispiste on tiukassa nipussa ikäluokkien a3 ja a4 kanssa aivan origon vasemmalla puolella. Miesten keskiarvopiste on hieman origosta oikealle, yhdessä ikäluokan a5 kanssa.

Lisäpisteet on hyvin esitetty, niiden etäisyyksiä voi luotettavasti arvioida kuvasta. Poikkeus on nuorin ikäluokka (a1, qlt = 501). Inertian osuudet (inr) ovat yhtä vaatimattomia kuin Belgian (28) ja Saksan (29), (m =20, f = 17, a2 = 40, a6 = 83), samoin kontribuutiot akseleiden inertiaan. 1. dimension kontribuutio (ctr) on suuri (>800) kaikilla paitsi nuorimmalla ikäryhmällä (a1) jolla 2. dimension selittää lähes puolet sen inertiasta (470). En esitä numeerisia tuloksia tarkemmin.

Karttaa 7.2 voi verrata karttaan 5.1, jossa on esitetty iän ja sukupuolen yhteisvaikutusmuuttuja. Pinottu taulu on vaihtoehtoinen tapa, ja kartasta 7.2 voi päätellä samat asiat: miehet ovat konservatiivisempia kuin naiset, iäkkäämmät ovat konservatiivisempia kuin nuoret. Nuorin ikäluokka poikkeaa muista.

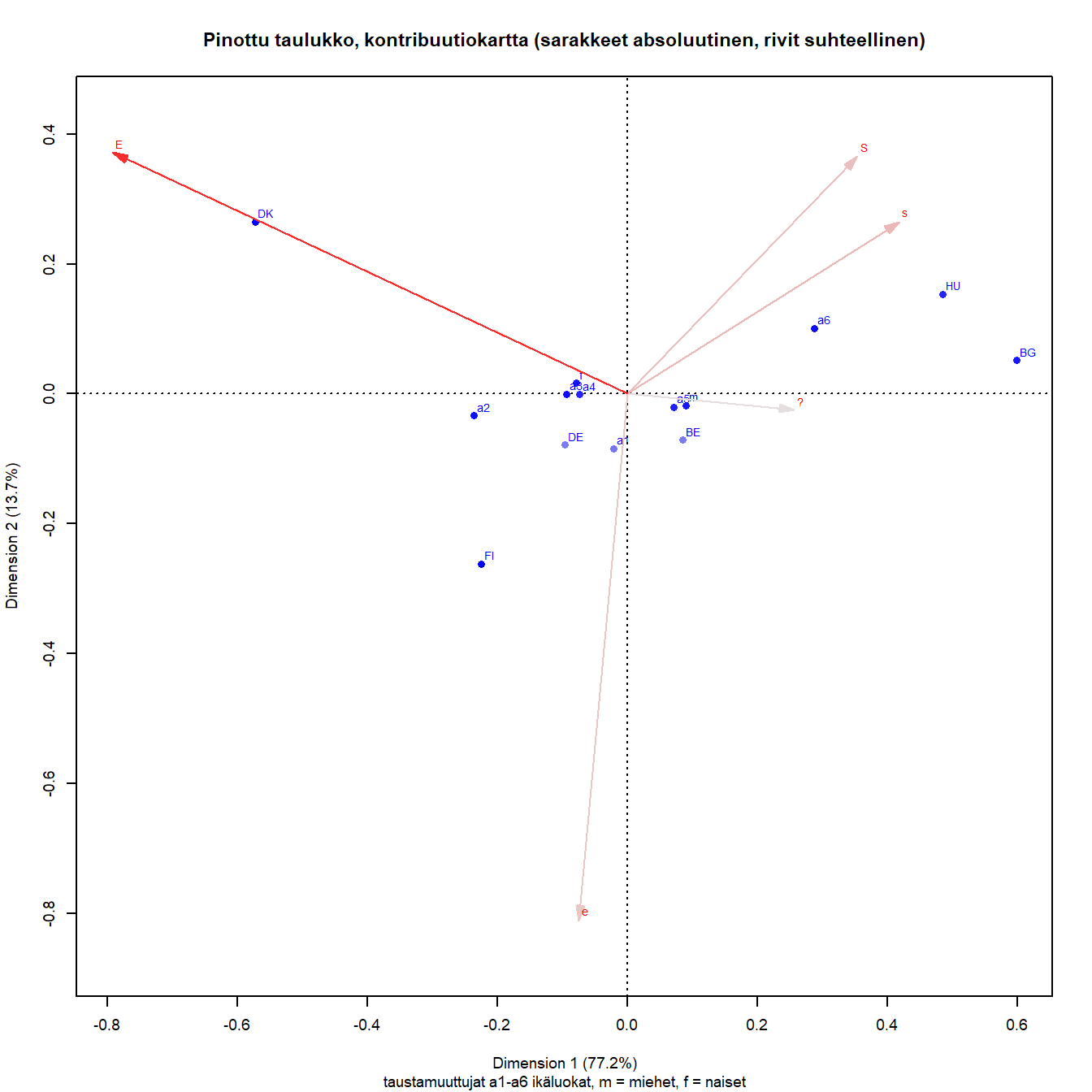
Kuva 7.3: Q1b: Lapsi kärsii jos äiti käy työssä

Kontribuutionkartan (Kuva 7.3) sarakkeista E-sarake (täysin eri mieltä) määrittää akseleita vahvasti, kontrastina kaksi konservatiivista vastausta (S ja s) ja myös neutraali vaihtoehto (e). Numeeriset tulokset kertovat, että ikäluokat vaikuttavat juuri ensimmäiseen tärkeimpään dimensioon.

Belgian ja Saksan pisteet on esitetty kartassa huonosti, samoin nuorin ikäluokka. Muiden pisteiden sijaintia voidaan arvioida myös sarakkeiden ja rivipisteiden välillä. Ikäluokkien kontrasti on selvä toiseksi nuorimman (a2) ja vanhimman (a6) välillä.

Kontribuutiokartalla voi arvioida hieman tarkemmin ikäluokkien ja vastausvaihtoehtojen yhteyttä sarake kerrallaan. Maltillisesti eri mieltä olevien osuus on suhteellisesti suurin nuorimmassa ikäluokassa. Jos a1 - pisteen projisoi konservatiivisen S-vastauksen janalle se ei ikäluokista konservatiivisin. Ikäluokat a2 ja a6 ovat ääripäitä, muut ikäluokat sijoittuvat lähelle toisiaan mutta liberaalille puolelle.

Esimerkkiaineistossa ei ole puuttuvia tietoja. Ne olisivatkin pulmallisia, varianssin dekomponointi ei onnistu, jos reunajakaumat ovat alitaulukoissa selvästi erilaisia.

Matriisien yhdistely on monipuolinen laajennus. Eräs kiinnostava malli on ABBA, kahden rakenteeltaan samanlaisen matriisin yhdistäminen lohkoina. Nimi kertoo yhdistetyn matriisin rakenteen (block circulant matrix), päällekkäin pinotut A ja B liitetään toiseen pinottuun matriisiin B ja A. Matriiseilla on samat rivit ja sarakkeet, esimerkiksi miesten ja naisten vastausprofiilit yhteen kysymykseen maittain luokiteltuina. Kokonaisinertia saadaan dekomponoitua ryhmien sisäiseen ja väliseen hajontaan kahdelle kartalle. Toinen kuvaa maiden välisiä eroja ja toinen maiden sisäisiä sukupuolten välisiä eroja (CAiP ss. 177-).

7.2 Monimuuttujakorrespondenssianalyysi (MCA)

MCA on yhdistettyjen (”pinottujen”) taulukoiden erikoistapaus, samantyyppiset muuttujat taulukoidaan keskenään. Tulos riippuu siis vain muuttujien parittaisista yhteyksistä.

Tätä ”supertaulukkoa” kutsutaan Burtin matriisiksi. Indikaattorimatriisi on toinen tapa esittää data. Indikaattorimatriisin sarakkeet ovat luokittelumuuttujan arvoja (kategorioita) ja rivit yksittäisiä vastausprofiileja. Profiilissa on rivi nollia ja ykkösiä, 1 valitun vaihtoehdon sarakkeessa.

En tässä jaksossa esitä numeerisia tuloksia, mutta niiden tutkimisella voi jatkaa analyysiä.

Tavoite on tutkia seitsemän kysymyksen vastausvaihtoehtojen yhteyksiä, miten ne asettuvat kaksiulotteiselle kartalle. Aikaisemmissa luvuissa etsittiin yhteyksistä uusia piirteitä ja tarkennettiin analyysiä. Nyt hahmotetaan ison aineiston muuttujien välisiä yhteyksiä ja erityisesti puuttuvien tietojen ongelmaa.

Koko datassa (kts. luku 2) on 32823 havaintoa 25 maasta. Niistä täydellisiä on 71 prosenttia. Jos valitaan kuusi taustamuuttujaa (edu, sosta, urbru, maa, ika, sp) ja seitsemän kysymystä, täydellinen havaintoja on 81 prosenttia.

Pelkissä kysymyksissä (Q1a, Q1b, Q1c, Q1d, Q1e, Q2a, Q2b) puuttuvia tietoja on 14 prosentissa havaintoja (4554). Kaikkien puutteellisten havaintojen poistamien (”listwise delete”) on sitä huonompi vaihtoehto mitä enemmän muuttujia on.

Kaikissa kysymyksissä on viisi vastausvaihtoehtoa ja kuudes kategoria puuttuvalle tiedolle.

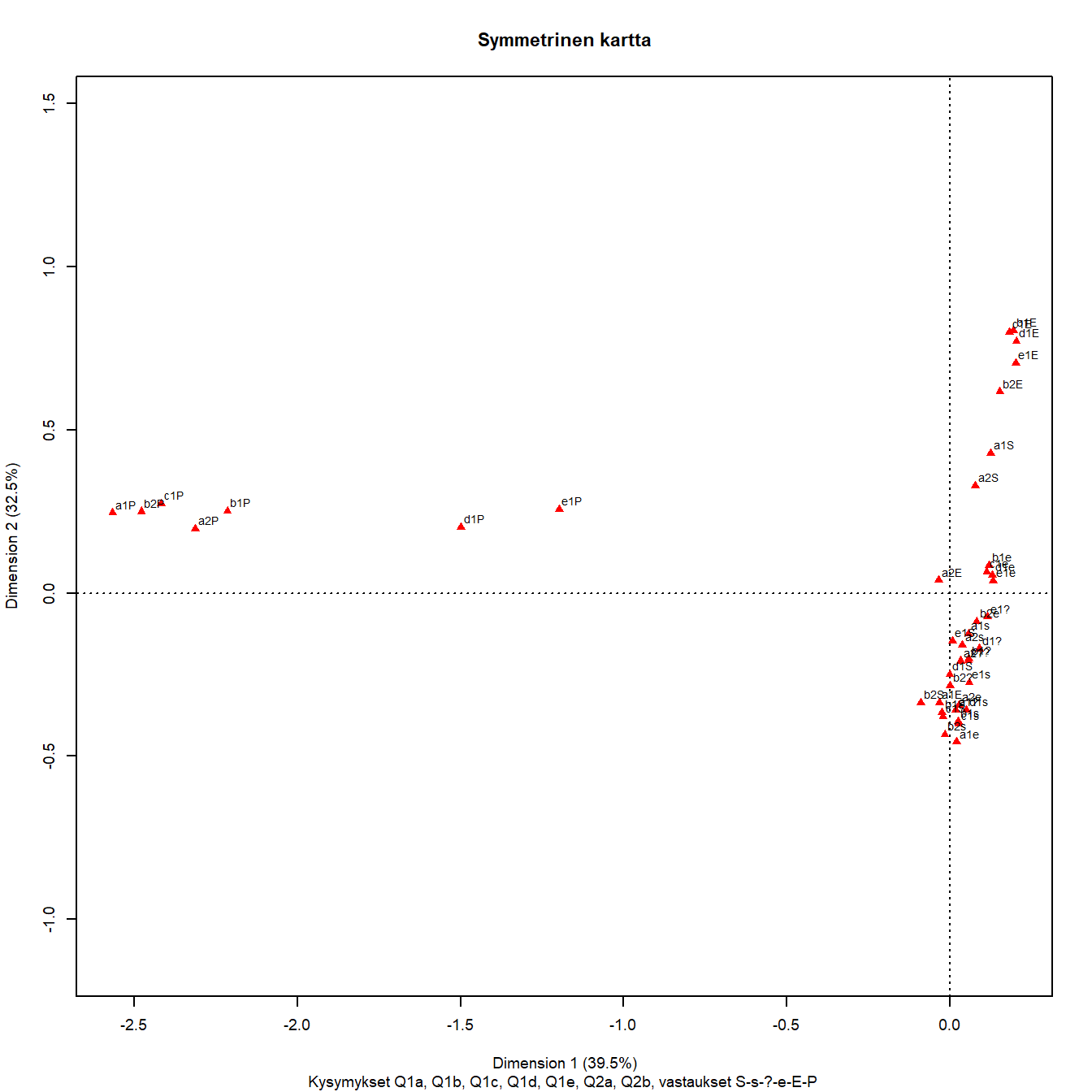
Kuva 7.4: MCA: Seitsemän kysymystä - 25 maata, kartta 1

Kuvasta 7.4 nähdään, että inertian selitysosuudet ovat paljon pienempiä, ja ratkaisu on selvästi kaksiulotteinen. Puuttuvat vastaukset erottuvat omana ryhmänä, ja varsinaiset vastaukset ovat pakkautuneet y-akselin oikealle puolelle. Niiden erot näkyvät vain toisessa dimensiossa. Ensimmäinen dimensio kuvaa vastaamattomuutta, kontrastina kaikki vastauskategoriat. Kokonaisinertiaa on korjattu pienemmäksi (ns. adjusted inetia, kts. liite 1).

Pystyakselin suuntaan kontrasti näyttäisi olevan konservatiiviset ylhäällä, modernit ja liberaalimmat alhaalla. Pisteitä on vaikea erottaa toisistaan.

Karttaa voi parantaa lisäämällä siihen vastaajien pisteet.

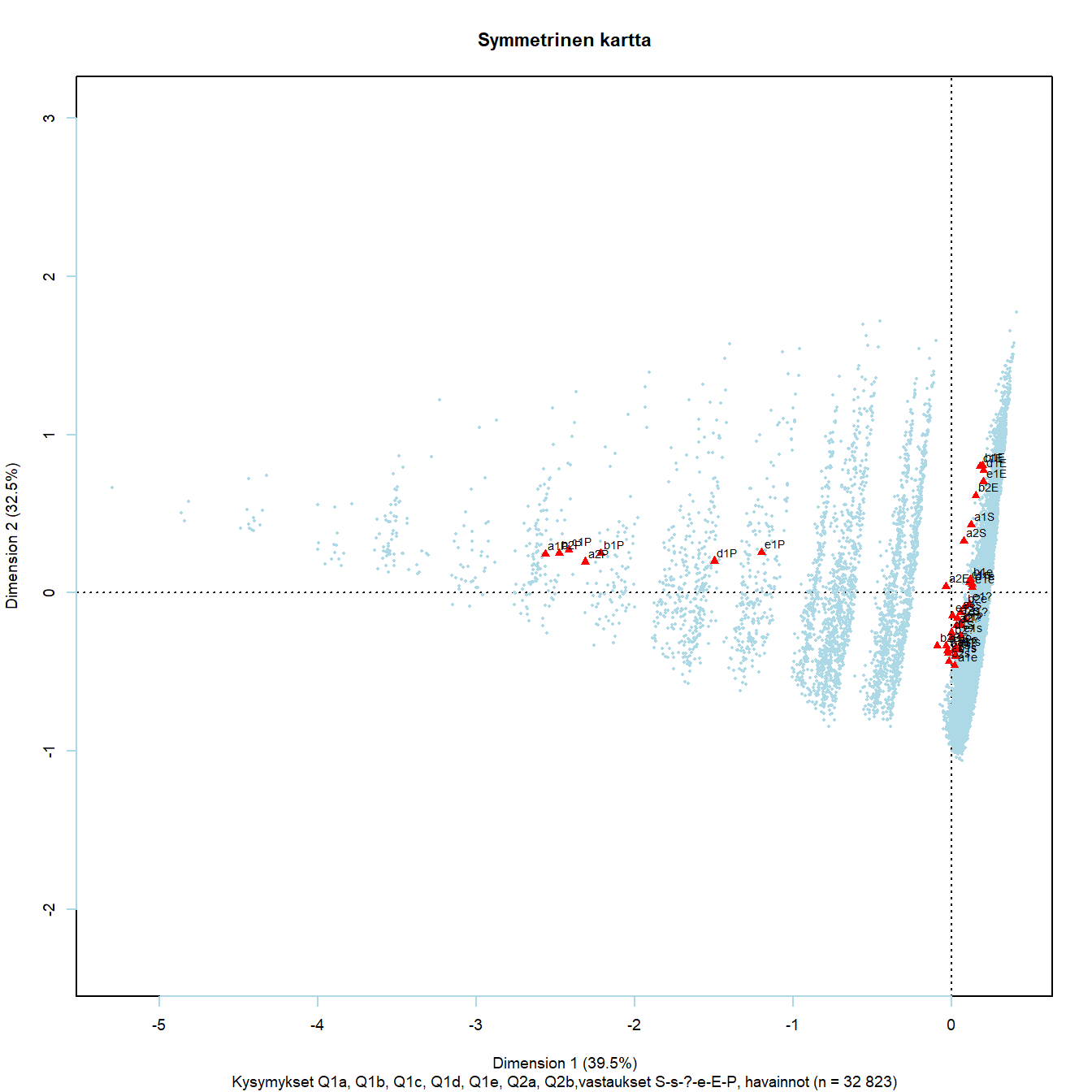
Kuva 7.5: MCA: Seitsemän kysymystä - 25 maata, kartta 2

Kuvassa 7.5 jokainen havainto on sarakevektoreiden keskiarvopiste. Sarakevektoreita ei voi tulkita yhtä selkeästi kuin yksinkertaisessa korrespondenssianalyysissä. Ne eivät edusta kysymystä vaan kysymyksen yhtä vastauskategoriaa.

Pistepilven muoto näyttää, miten pienenevä joukko vastaajia lähestyy kiilana puuttuvien tietojen pisteitä. Kaikkiin kysymyksiin vastanneet ovat massana kuvan oikeassa laidassa. Pistepilvet oikealta vasemmalle kuvaavat kuinka moneen kysymykseen on jätetty vastaamatta.

Osajoukon MCA

Osajoukon MCA sopii hyvin sekä puuttuvien tietojen että täydellisten vastausten analyysiin. Asymmetrisessä kartassa sarakkeet skaalautuvat pois origosta, ja näkyvät paremmin. Kuvaan 7.6 on piirretty havaintopisteet, joista voi hahmottaa havaintojen sijoittumista kartalla.

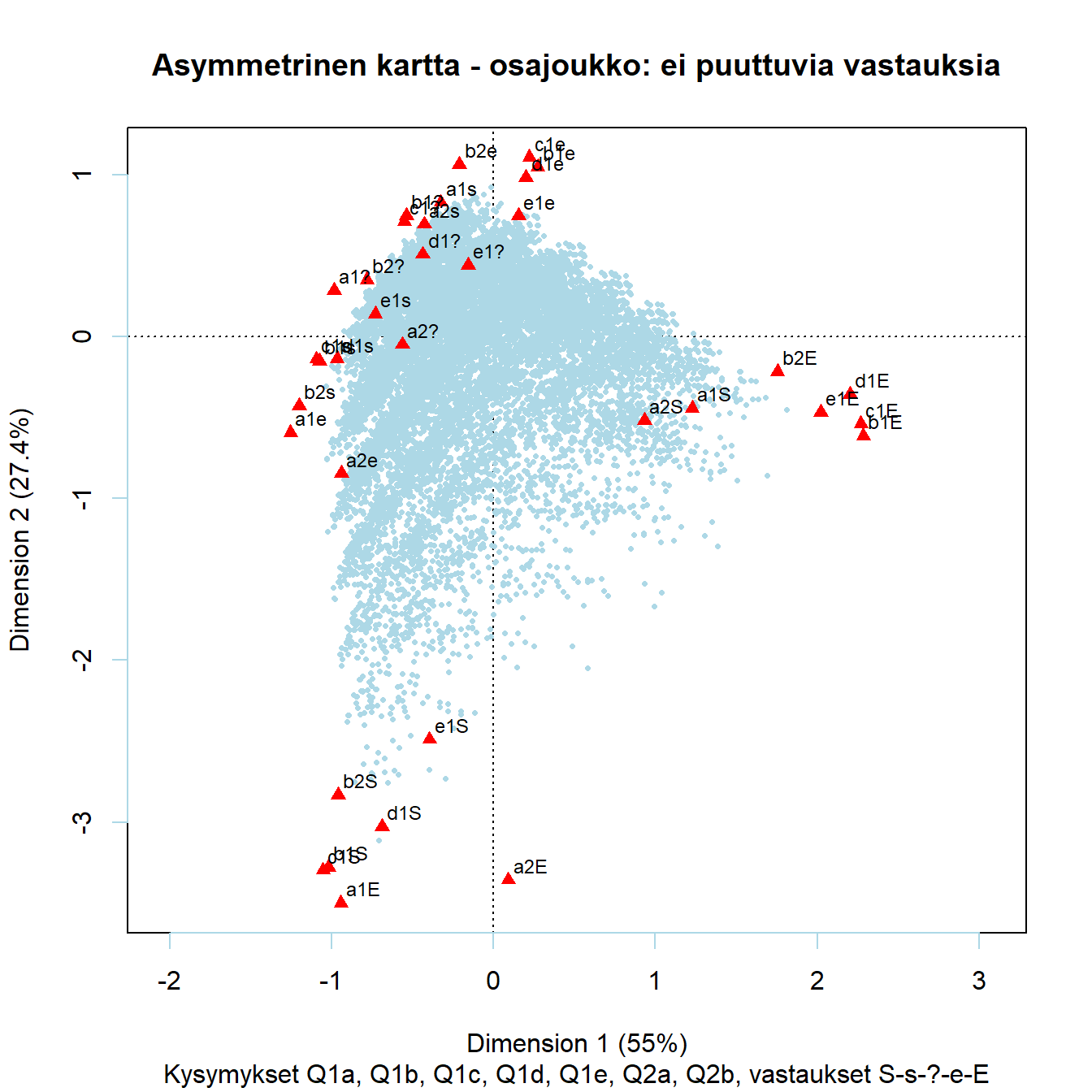
Kuva 7.6: MCA: Seitsemän kysymystä - 25 maata, kartta 3

Kontrasti on “ääripäiden” välillä, vahvat mielipiteet (S ja E) hallitsevat vasenta alakulmaa ja oikeaa laitaa x-akselin tuntumassa. Maltilliset vastaukset ja neutraali vaihtoehto ovat ylhäällä vasemmalla. Liberaalit vastaukset ovat oikealla ylhäällä ja jokaiselle löytää vastinparin vasemmalta alhaalta, konservatiivien kulmasta. Konservatiivisten vastausten joukosta lähimpänä liberaalia ryvästä on “e1S” (“Kotirouvana oleminen on aivan yhtä antoisaa kuin ansiotyön tekeminen” - täysin samaa mieltä). Vastaavasti “a2S” (“Sekä miehen että naisen tulee osallistua perheen toimeentulon hankkimiseen” - täysin samaa mieltä) on lähimpänä konservatiivista kulmaa. Molemmat “ääripäiden maltilliset” pisteet ovat myös omassa ryhmässään lähimpänä maltillisten ja neutraalien vastausten ryhmää.

Karttaan voi hahmotella diagonaalin suuntaisen akselin vahvojen mielipiteiden ryppäiden välille. Muut vastaukset ovat mukaisesti näiden välisellä kaarevalla linjalla (Guttman-efekti).

Greenacre (2010) (s. 139-) analysoi lähes samoja kysymyksiä ISSP-datalla 2002. Tulokset ovat hyvin samantapaisia. Karttaa 7.6 vastaavan kuvan jatkoanalyysi on vasemman yläkulman pisteiden tarkempi analyysi. Greenacre havaitsee, että nämä neutraalit ja maltilliset vastaukset eivät ole hyvin esitettyjä kaksiulotteisella kartalla, vaan ne karkaavat korkeampiin ulottuvuuksiin (“dimensions of middleness”).

Tässä aineistossa kolmiulotteinen MCA antaa samantapaisia viitteitä, mutta vain osa keskikategorioista on huonosti esitetty myös siinä. Huono kvaliteetti on vain osalla sarakkeita (e1? 475, c1? 71 ja b1? 573).

Luku 8 Yhteenveto

Tutkielman data-analyysi päättyi vaiheeseen, josta voi jatkaa laajan aineiston analyysiä. Analyysin kysymykset näyttävät erottelevan hyvin ja johdonmukaisesti vastaajat konservatiivisen ja liberaalimman modernimman mielipiteen välillä. Neutraali vaihtoehto ja ”dimensios of middleness” kannattaa huomioida. Puuttuvat tiedot voi korrespondenssianalyysissä analysoida omana osajoukkona ja päättää miten menettelee.

Korrespondenssianalyysi sopii hyvin yksinkertaisen kahden luokittelumuuttujan riippuvuuksien visualisointiin. Kuvan oikea analyysi onnistuu pienellä harjoittelulla. Tämä ei ole mitätön asia, taulukoita on kaikkialla. Menetelmä laajenee joustavasti myös mutkikkaampiin tutkimusasetelmiin.

Useiden muuttujien samanaikainen analyysi onnistuu kahdella tavalla, taulukoita yhdistelemällä tai monimuuttujakorrespondenssianalyysillä (MCA). Tulkinta muuttuu vaativammaksi, mutta MCA-esimerkki luvussa 7 esittää myös menetelmän pätevyyden.

Aineiston sisällöllisesti tärkeät muuttujat ovat järjestysasteikon muuttujia. Tutkimusasetelmissa vertailtiin eri ryhmiä ja kuvattiin niiden yhteyksiä vastauskategorioihin. Korrespondenssianalyysi on luokitteluasteikon muuttujille sopiva menetelmä, järjestysasteikon muuttujien ”oikeita etäisyyksiä” voidaan arvioida.

Data-analyysi osoitti, että maiden tai muiden ryhmien vertailu ei ole niin yksinkertaista kuin ehkä luullaan. Blasius ja Thiessen (2006) tutkivat MCA-menetelmällä ISSP:n 1994 kerättyä aineistoa. He osoittavat, että datan laatu ja rakenne vaihtelee paljon maiden välillä (”…both the quality of the data, as well as its underlying structure - and therefore meaning - vary considerably between countries.”).

Datan laadun ja rakenteen lisäksi järjestysasteikon käyttöön liittyy yleisempi ongelma. Voiko vastaajien ryhmiä vertailla keskenään järjestysasteikollisen muuttujan jonkinlaisilla keskiarvoilla? Bond ja Lang (2018) osoittavat että tämä onnistuu vain harvoin. “Our goal is not to provide a litany of concerns – which can be done for most social scientific metrics – but rather to establish that standard happiness measures cannot rank the average happiness of two groups without strong additional assumptions about the underlying distribution of happiness. We expect that even if we achieve consensus on these assumptions, many comparisons will remain unranked.” Korrespondenssianalyysillä vertailun voi tehdä ilman jakaumaoletuksia, katsoa miltä data näyttää.

Lähteet

Blasius, Jörg, ja Victor Thiessen. 2006. ”Assessing Data Quality and Construct Comparability in Cross-National Surveys”. European Sociological Review 22 (3): 229–42. http://www.jstor.org/stable/3806519.

Bond, Timothy N., ja Kevin Lang. 2018. ”The Sad Truth About Happiness Scales”. Journal of Political Economy 127 (4): 1629–40. https://doi.org/10.1086/701679.

Ferragina, Emanuele, ja Martin Seeleib-Kaiser. 2015. ”Determinants of a Silent (R)evolution: Understanding the Expansion of Family Policy in Rich OECD Countries”. Social Politics: International Studies in Gender, State and Society 22 (1): 1–37. https://doi.org/10.1093/sp/jxu027.

Gendall, Phil, ja Martin von Randow. 2016. ”International Social Survey Programme , ISSP 2012 - Family and Changing Gender Roles IV, Study Monitoring Report”. https://dbk.gesis.org/dbksearch/sdesc2.asp?no=5900&db=e&doi=10.4232/1.12661.

GESIS. 2016. ”ISSP 2012 - Family and Changing Gender Roles IV, Variable Report”. GESIS. https://doi.org/10.4232/1.12661.

Greenacre, Michael. 2003. ”Singular value decomposition of matched matrices”. Journal of Applied Statistics 30 (10): 1101–13. https://doi.org/10.1080/0266476032000107132.

———. 2006. ”Tying up the loose ends in simple, multiple, joint correspondence analysis”. Teoksessa Compstat 2006 - Proceedings in Computational Statistics, toimittanut Alfredo Rizzi ja Maurizio Vichi, 163–85. Heidelberg: Physica-Verlag HD.

———. 2013. ”Contribution Biplots”. Journal of Computational and Graphical Statistics 22 (1): 107–22. https://doi.org/10.1080/10618600.2012.702494.

———. 2017. ”Multiple Correspondence Analysis (MCA): Theory and Practice, spring 2017 (University of Helsinki )”. https://moodle.helsinki.fi/course/search.php?search=correspondence+analysis.

Greenacre, Michael, ja Jörg Blasius. 2006. Multiple correspondence analysis and related methods. Boca Raton (FL): Chapman; Hall/CRC. https://helka.finna.fi/Record/helka.2018050.

Greenacre, Michael, ja Trevor Hastie. 1987. ”The Geometric Interpretation of Correspondence Analysis”. Journal of the American Statistical Association 82 (398): 437–47. https://doi.org/10.1080/01621459.1987.10478446.

Greenacre, Michael J. 1989. ”The Carroll-Green-Schaffer Scaling in Correspondence Analysis: A Theoretical and Empirical Appraisal”. Journal of Marketing Research 26 (3): 358–65. https://doi.org/10.1177/002224378902600310.

———. 2010. Biplots in Practice. Bilbao, Spain: Fundacion BBVA. https://www.fbbva.es/microsite/multivariate-statistics/biplots.html.

———. 2017. Correspondence analysis in practice. Third edition. Boca Raton, Florida: CRC Press. https://helka.finna.fi/Record/helka.3029760.

———. 2018. Compositional data analysis in practice. Boca Raton, Florida: CRC Press. http://bvbr.bib-bvb.de:8991/F?func=service&doc_library=BVB01&local_base=BVB01&doc_number=030915862&sequence=000001&line_number=0001&func_code=DB_RECORDS&service_type=MEDIA.

Greenacre, Michael, ja Rafael Pardo. 2006. ”Subset Correspondence Analysis: Visualizing Relationships Among a Selected Set of Response Categories From a Questionnaire Survey”. Sociological Methods & Research 35 (2): 193–218. https://doi.org/10.1177/0049124106290316.

Greenacre, Michael, ja Raul Primicerio. 2013. Multivariate Analysis of Ecological Data. Bilbao: Fundacion BBVA. https://www.fbbva.es/microsite/multivariate-statistics/maed.html.

ISSP. 2016. ”ZA5900: International Social Survey Programme: Family and Changing Gender Roles IV - ISSP 2012 - data ja dokumentaatio (selattava versio)”. https://zacat.gesis.org/webview/index.jsp?object=http://zacat.gesis.org/obj/fStudy/ZA5900.

”ISSP 2012 - Family and Changing Gender Roles IV Basic Questionnaire”. 2011. https://dbk.gesis.org/dbksearch/sdesc2.asp?no=5900&db=e&doi=10.4232/1.12661.

LeRoux, Brigitte, ja Henry Rouanet. 2004. Geometric data analysis: from correspondence analysis to structured data analysis. Dordrecht: Kluwer Academic Publishers.

McNamara, Amelia, ja Nicholas J. Horton. 2018. ”Wrangling Categorical Data in R”. The American Statistician 72 (1): 97–104. https://doi.org/10.1080/00031305.2017.1356375.

Mustonen, Seppo. 1995. Tilastolliset monimuuttujamenetelmät. Helsinki: Survo Systems. http://www.survo.fi/mustonen/monim.pdf.

Nenadic, O., ja M. Greenacre. 2007. ”Correspondence Analysis in R, with two- and three-dimensional graphics: The ca package”. Journal of Statistical Software 20 (3): 1–13. http://www.jstatsoft.org.

Scholz, Evi, Regina Jutz, Jonas Edlund, Ida Öun, ja Michael Braun. 2014. ”ISSP 2012 Family and Changing Gender Roles IV: Questionnaire Development”. https://explore.openaire.eu/search/publication?articleId=od______1272::0a6c70387bf644137af3cb2bc69b0df6.

Smith, Tom W. 2015. ”International Social Survey Programme”. International Encyclopedia of the Social & Behavioral Sciences (Second Edition). https://doi.org///doi-org.libproxy.helsinki.fi/10.1016/B978-0-08-097086-8.44080-8.

Tilastokeskus. 2012. ”ISSP 2012 - Family and Changing Gender Roles IV Questionnaire (Finnish)”. Tilastokeskus. https://zacat.gesis.org/webview/index.jsp?object=http://zacat.gesis.org/obj/fStudy/ZA5900.

Vehkalahti, Kimmo. 2008. Kyselytutkimuksen mittarit ja menetelmät. Helsinki: Tammi. https://helka.finna.fi/Record/helka.2120450.

Walter, Jessica. 2018. ”The adequacy of measures of gender roles attitudes: a review of current measures in omnibus surveys”. Quality & Quantity 52 (2): 829–48. https://doi.org/10.1007/s11135-017-0491-x.

Xie, Yihui. 2016. bookdown: Authoring Books and Technical Documents with R Markdown. Chapman; Hall/CRC. https://bookdown.org/yihui/bookdown/.

Liite 1: Korrespondenssianalyysin teoriaa

Korrespondenssianalyysin perusyhtälöt ja kaavat

Perusyhtälöt on esitetty teoksen “Correspondece Analysis in Practice”(M. J. Greenacre 2017) liitteen “Theory of Correspondece Analysis” mukaisesti.

Datamatriisilla \(\boldsymbol{N}\) on \(I\) riviä ja \(J\) saraketta (\(I x J\)). Alkiot ovat ei-negatiivisia ja samassa mitta-asteikossa. Jos mitta-asteikko on intervalli- tai suhdeasteikko, mittayksiköiden on oltava samoja (esim. euroja, metrejä). Tietyin ehdoin myös negatiiviset luvut ovat sallittuja (LeRoux ja Rouanet 2004, 60).

Taulukon alkioiden summa on \(\sum_{i} \sum_{j}n_{ij} = n\), missä \(i = 1, \dots , I\) ja \(j = 1, \dots , J\).

Korrespondenssimatriisi \(\boldsymbol{P}\) saadaan jakamalla matriisin \(\boldsymbol{N}\) alkiot niiden summalla \(n\) .

Merkitään matriisin \(\boldsymbol{P}\) rivisummien vektoria \(\boldsymbol{r}\) (= \((r_{1}, \dots, r_{I})\)) ja sarakesummien vektoria \(\boldsymbol{c}\) (= \((c_{1}, \dots, c_{J})\)). Niitä vastaavat diagonaalimatriisit ovat \(\boldsymbol{D_r}\) ja \(\boldsymbol{D_c}\).

Matriisin transpoosi merkitään yläindeksillä \(T\), ja \(\boldsymbol{1}\) on sopivan dimension vektori, jonka alkiot ovat ykkösiä.

Korrespondenssianalyysin ratkaistaan singulaariarvohajotelman (singular value decomposition, SVD) avulla.

Singulaariarvohajotelma tuottaa ratkaisun, kun sitä sovelletaan standardoituun residuaalimatriisiin \(\boldsymbol{S}\).

\[\begin{equation} \boldsymbol{S} = \boldsymbol{D_r}^{-1/2}(\boldsymbol{P} - \boldsymbol{r}\boldsymbol{c}^T)\boldsymbol{D_c}^{-1/2} . \tag{8.1} \end{equation}\]

Residuaalimatriisi voidaan esittää myös ns. kontingenssi-suhdelukujen (contingency ratio) avulla kahdella tavalla.

\[\begin{equation} \boldsymbol{D_r}^{-1} \boldsymbol{P} \boldsymbol{D_c}^{-1} = \left( \frac{p_{ij}} {r_{i} c{j}} \right) , \tag{8.2} \end{equation}\]

\[\begin{equation} \boldsymbol{S} = \boldsymbol{D_r}^{1/2} (\boldsymbol{D_r}^{-1} \boldsymbol{P} \boldsymbol{D_c}^{-1} - \boldsymbol{1}\boldsymbol{1}^{T} ) \boldsymbol{D_c}^{-1/2} \;\;\; . \tag{8.3} \end{equation}\]

Toinen esitystapa on hyödyllinen, kun tarkastellaan CA:n yhteyksiä muihin läheisiin menetelmiin. Näitä ovat esimerkiksi “suhteellisten osuuksien datan” analyysi (log ratio analysis of compositiona data), moniulotteinen skaalaus, lineaarinen diskriminanttianalyysi, kanoninen korrelaatioanalyysi, pääkomponenttianalyysi, kaksoiskuvat ja muut SVD-hajotelmaan perustuvat dimensioiden vähentämisen menetelmät.

Samat kaavat voi esittää myös alkiomuodossa:

\[\begin{equation} s_{ij} = \frac{p_{ij}-r_{i}c_{j}} { \sqrt{r_{i}c_{j} } } , \tag{8.4} \end{equation}\]

\[\begin{equation} s_{ij} = \sqrt{r_{i}} \left( \frac{p_{ij}}{r_{i}c_{j}} \right) \sqrt{c_{j}} \;\;\; . \tag{8.5} \end{equation}\]

Alkiomuodossa esitetyistä kaavoista näkee rivi- ja sarakeratkaisujen sidoksen. Ratkaisujen duaalisuus on teoreettinen tulos, jonka voi perustella täsmällisesti algebrallisen geometrian avulla. Käytännössä rivi- ja sarakeongelman duaalisuus tarkoittaa sitä, että vain toinen ongelma on ratkaistava.

Singulaariarvohajotelma matriisille \(\boldsymbol{S}\) on

\[\begin{equation} \boldsymbol{S} = \boldsymbol{U} \boldsymbol{D_{\alpha}} \boldsymbol{V}^{T} , \tag{8.6} \end{equation}\]

missä \(\boldsymbol{D_{\alpha}}\) on diagonaalimatriisi, jonka alkiot ovat singulaariarvot suuruusjärjestyksessä \(\alpha_{1}\geq \alpha_{1} \geq \cdots\).

Matriisit \(\boldsymbol{U}\) ja \(\boldsymbol{V}\) ovat ortogonaalisia singulaarivektoreiden matriiseja. Singulaariarvohajotelman merkitys dimensioiden vähentämiselle perustuu Eckart - Young - teoreemaan. Teoreema kertoo että saamme pienimmän neliösumman \(m\) - ulotteisen approksimaation matriisille \(\boldsymbol{S}\) matriisien \(\boldsymbol{U}\) ja \(\boldsymbol{V}\) ensimmäisten sarakkeiden ja ensimmäisten singulaariarvojen avulla.

\[\begin{equation} \boldsymbol{S}_{(m)} = \boldsymbol{U}_{(m)} \boldsymbol{D}_{\alpha(m)} \boldsymbol{V}_{(m)}^{T} \tag{8.7} \end{equation}\]

Korrespondenssianalyysin ratkaisualgoritmissa tätä tulosta on muokattava niin, että rivien ja sarakkeiden massat huomioidaan pienimmän neliösumman approksimaatiossa painoina.

Näin saadaan standardikoordinaatit ja pääkoordinaatit riveille ja sarakkeille.

Rivien standardikoordinaatit

\[\begin{equation} \boldsymbol{\Phi} = \boldsymbol{D_r}^{-\frac{1}{2}} \boldsymbol{U} \tag{8.8} \end{equation}\]

Sarakkeiden standardikoordinaatit

\[\begin{equation} \boldsymbol{\Gamma} = \boldsymbol{D_c}^{-\frac{1}{2}} \boldsymbol{V} \tag{8.9} \end{equation}\]

Rivien pääkoordinaatit

\[\begin{equation} \boldsymbol{F} = \boldsymbol{D_r}^{-\frac{1}{2}} \boldsymbol{U} \boldsymbol{D_{\alpha}} = \boldsymbol{\Phi} \boldsymbol{D_{\alpha}} \tag{8.10} \end{equation}\]

Sarakkeiden pääkoordinaatit \[\begin{equation} \boldsymbol{G} = \boldsymbol{D_c}^{-\frac{1}{2}} \boldsymbol{V} \boldsymbol{D_{\alpha}} = \boldsymbol{\Gamma} \boldsymbol{D_{\alpha}} \tag{8.11} \end{equation}\]

Pääakseleiden inertiat (principal inertias) \(\lambda_{k}\)

\[\begin{equation} \lambda_{k} = \alpha_{k}^2, \: k = 1,\dots,K, K = min \{ I-1, J-1 \} \end{equation}\]

Ratkaisun dimensio on myös maksimi-inertia. Tässä aineistossa ja vastaavissa kyselytutkimusdatoissa inertia on yleensä paljon maksimia pienempi. Asymmetrisissä kartoissa ideaalipisteet ovat kaukana origon lähelle pakkautuneesta havaintojen pilvestä.

Korrespondenssianalyysi ratkaisun akseleiden inertioita kutsutaan usein ominaisarvoiksi, mutta periaatteessa SVD-ratkaisulla saadaan singulaariarvot. Niiden neliöt ovat akseleiden inertioita. Ominaisarvojen ja singulaariarvojen yhteys on läheinen ja riippuu diagonalisoitavan matriisin ominaisuuksista. Termiä “vektori” käytetään kartoista puhuttaessa, kun viitataan esimerkiksi origosta sarakepisteeseen piirrettyyn nuoleen. Myös janan synonyyminä käytetään yleisesti termiä vektori (kts. esim. (M. Greenacre 2013)).

Korrespondenssimatriisi \(\boldsymbol{P}\) voidaan esittää matriisi- ja alkiomuodossa ns. palautuskaavana (reconstitution formula).

\[\begin{equation} \boldsymbol{P} = \boldsymbol{D}_{r} \left( \boldsymbol{1}\boldsymbol{1}^{T} + \boldsymbol{\Phi}\boldsymbol{D}_{\lambda}^{\frac {1}{2}}\boldsymbol{\Gamma}^{T}\right)\boldsymbol{D}_{c} \tag{8.12} \end{equation}\]

\[\begin{equation} p_ {ij}= r_{i}c_{j} \left(1 + \sum_{k=1}^{K} \sqrt{\lambda_{k}} \phi_{ik} \gamma_{jk} \right) \tag{8.13} \end{equation}\]

Rivien ja sarakkeiden riippuvuutta kuvaavat transitioyhtälöt (transition equations).

Pääkoordinaatit standardikoordinaattien funktiona (barysentrinen ominaisuus, barycentric relationships):

\[\begin{equation} \boldsymbol{F} = \boldsymbol{D}_{r}^{-1} \boldsymbol{P}\boldsymbol{\Gamma} \tag{8.14} \end{equation}\]

\[\begin{equation} \boldsymbol{G} = \boldsymbol{D}_{c}^{-1} \boldsymbol{P}^{T}\boldsymbol{\Phi} \tag{8.15} \end{equation}\]

Pääkoordinaatit pääkoordinaattien funktiona:

\[\begin{equation} \boldsymbol{F} = \boldsymbol{D}_{r}^{-1} \boldsymbol{P}\boldsymbol{G}\boldsymbol{D}_{\lambda}^{-\frac{1}{2}} \tag{8.16} \end{equation}\]

\[\begin{equation} \boldsymbol{G} = \boldsymbol{D}_{c}^{-1} \boldsymbol{P}^{T}\boldsymbol{F}\boldsymbol{D}_{\lambda}^{-\frac{1}{2}} \tag{8.17} \end{equation}\]

Yhtälöt (8.14) ja (8.14) esittävät profiilipisteet ideaalipisteiden (vertex points) painotettuina keskiarvoina, painoina profiilin elementit. Asymmetriset kartat (rivien tai sarakkeiden suhteen) perustuvat näihin yhtälöihin. Yhtälöiden (8.16) ja (8.17) kahdet pääkoordinaatit ovat perusta symmetrisille kartoille. Myös niitä yhdistää barysentrinen painotetun keskiarvon riippuvuus, mutta mukana ovat skaalaustekijät \(\frac{1}{\sqrt{\lambda_{i}}}\).

Pisteet ja projektio aliavaruuteen

Kuva on kurssimateriaaleista (M. Greenacre 2017).

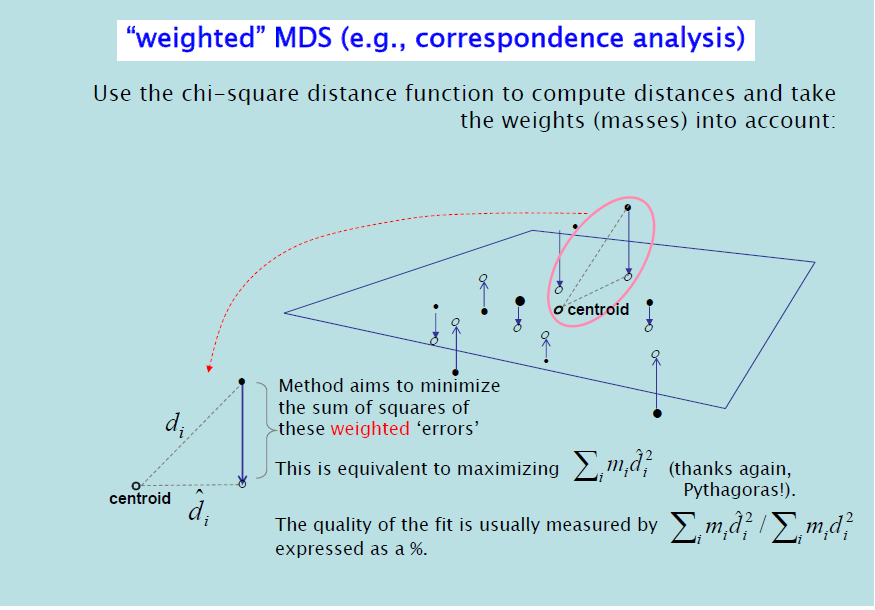
Kuva 8.1: Pisteen projektio aliavaruuteen

Kuvassa on esitetty korrespondenssianalyysin ratkaisun minimointiongelma. Pisteen projektio on sitä parempi mitä pienempi kulma on sentroidista pisteeseen piirretyn janan ja pisteen projektion välillä. cor-tunnusluku ca-funktion numeerisissa tuloksissa tämän kulman kosinin neliö. Pisteen kuvauksen laatu (qlt) ca-tuloksissa on valitun approksimaation akseleiden kvaliteettien (cor) summa.

Kuvasta voi myös hahmottaa sen periaatteen, että projektiossa kaukana olevat pisteet ovat kaukana myös alkuperäisessä avaruudessa. Projektiossa lähekkäin olevat pisteet voivat olla alkuperäisessä avaruudessa kaukana toisistaan, jos niiden projektion laatu on huono.

Monimuuttujakorrespondenssianalyysi MCA

Usean muuttujan korrespondenssianalyysissä tutkitaan usean muuttujan välisiä yhteyksiä. Kartan tulkinnan apuna siihen voidaan lisätä havaintojen sijaan niiden keskiarvopisteitä ja niille simuloituja luottamusellipsejä. Kuvien pääongelma on liian suuri määrä pisteitä, ja analyysin tavoite on usein mahdollisimman yksinkertainen kartta.

Usean muuttujan analyysissä kohteena on joko indikaattorimatriisi \(\boldsymbol{Z}\) tai Burtin matriisi \(\boldsymbol{B}\)

Indikaattorimatriisissa rivit ovat havaintoja ja sarakkeet luokittelumuuttujan arvoja. Havaintoa vastaa rivi nollia ja 1 valitun vastausvaihtoehdon kohdalla. Tästä seuraa, että vain erilaiset vastaukset määrittävät rivien etäisyyksiä.

Burtin matriisi on erikoistapaus yhdistetyistä matriiseista. Siihen on koottu kaikki tutkittavien muuttujien pareittain muodostetut taulukot. Diagonaalilla ovat muuttujien ristiintaulukoinnit itsensä kanssa. Ratkaisu riippuu vain näistä parittaisista taulukoista. Burtin matriisi on kätevä välivaihe matriisien yhdistelyssä.

Molemmat matriisit paisuttavat keinotekoisesti kokonaisinertiaa, ja esimerkiksi kaksiulotteisen kartan selitetyn inertian osuudet jäävät melko pieniksi. Ratkaisuna on inertian oikaisu tai korjaus (adjusted inertia), jossa mm. poistetaan kokonaisinertialaskelmista Burtin matriisin diagonaalilla olevat alimatriisit. Näillä korjauksilla ei ole vaikutusta kartan pisteiden sijaintiin. Tämä menetelmä on ca-paketin mjca-funktion oletus.

Kolmas vaihtoehto on ns. yhdistetty korrespondenssianalyysi (joint ca).

Greenacre on kirjoittanut useissa yhteyksissä MCA:n geometrisen tulkinnan ongelmista. Greenacre ja Hastie (1987) (s. 447) sanovat asian näin:“Finally, although we have motivated simple correspondence analysis from the geometric point of view, the geometry of the indicator matrix in multiple correspondence analysis is admittedly not convincing. Distances between the row profiles of an indicator matrix and projections of articficial column vertices have less intuitive appeal. However, the scaling interpretation remains attractive in this case; the displays are graphical representations of optimal scale values for the categories.”

Greenacre jatkaa samasta aiheesta artikkelikokoelmassa (M. Greenacre ja Blasius 2006 , s. 41, s. 61): “Yleistys useammalle kuin kahdelle muuttujalle ei ole ilmeinen eikä hyvin määritelty”. Silti MCA onnistuu esittämään hyvin kiinnostavia yhteyksiä muuttujien välillä (“succesfully recovers interesting patterns of association”). Kriittisyys ei kuitenkaan estä häntä soveltamasta MCA-analyysiä. Tulkitsen tämän niin, että menetelmää voi aivan hyvin soveltaa, mutta geometrista tulkintaa ei voi suoraan siirtää CA-kartoista MCA-karttoihin. Greenacre esittelee perusteellisesti MCA-sovelluksia kaksoiskuvia käsittelevässä kirjassaan (Greenacre 2010). Ehkä korrespondenssianalyysin matemaattinen teoria ei ole vielä täysin valmis?

Liite 2: Tekninen ympäristö ja Bookdown-paketti

Analysoin aineistoa r-paketilla ca, vaihtoehdoista voi mainita ranskalaisten kehittämän FactoMineR - paketin ja muitakin löytyy. Korrespondenssianalyysin voi tehdä myös monella muulla ohjelmistolla (esim. Survo, SAS ja SPSS). Greenacre ei ole tyytyväinen SPSS:n toteutukseen: “In SPSS’s CA program in the Categories module, an alternative biplot is given that has not been illustrated in this book, called the”symmetrical normalization“, which may be confused with the symmetric map described in this book. It is not exactly the same thing, however,since it uses standard coordinates scaled by the square roots of the singular values (i.e. fourth roots of the principal inertias) instead of the singular values themselves. Curiously, the symmetric map, one of the most popular display options of French researchers, has never been available in SPSS (module Categories), and it is still not possible in IBM SPSS version 20 to obtain a joint map of the rows and columns in principal coordinates”(CAiP, s. 296). En ole tarkastanut onko pitääkö kritiikki yhä paikkansa.

Bookdown

Bookdown-paketti laajentaa R-ohjelmiston julkaisuominaisuuksia (Xie 2016). Sen avulla voi tuottaa monipuolisesti julkaisuja samalla lähdekoodilla eri formaatteihin.

Html-formaatti sopii mainiosti data-analyysiin, taulukoita ja kuvia ei tarvitse asetella paperikoon mukaan sivuille. PDF-formaatilla on omat etunsa, koko dokumentti on yksi tiedosto. Olen käyttänyt bookdown-pakettia vailla suurempia ongelmia. Jos ongelmia tulee, niiden syiden selvittämien ei ole helppoa. Kuva 8.2 näyttää bookdown-paketin julkaisuprosessin vaiheet. PDF on ongelmallinen, tässä projektissa pdf-tulostus lakkasi toimimasta kaksi kertaa. Tutkielman pdf-versio on tulostettu selaimella bookdown-paketin tulostustvaihtoehdolla “html_book”.

Ongelmat ovat varmasti ratkaistavissa, ja bookdown-paketti tai sen muokatut versiot ovat laajassa käytössä monissa yliopistoissa. Kyse on vain LateX-osaamattomuudesta tai ymmärtämättömyydestä.

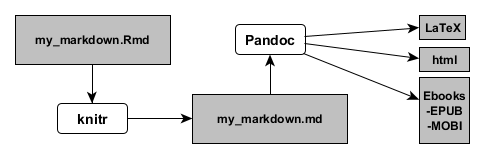
Kuva 8.2: Tulostiedoston prosessointi

Git ja Github

Käytin Github-palvelun versionhallintaa ja www-palvelua raporttien julkaisemiseen.

Tutkielman luonnos (https://hirjus.github.io/capaper/) ja lähdekoodi (https://github.com/hirjus/capaper) löytyvät sieltä. Data on pakattuna tiedostona.

Käyttöjärjestelmä ja R-ympäristö

RStudio-sovelluksen ja käyttämäni TeX-versiot ovat

RStudio Version 1.3.1093, latex engine xelatex

XeTeX, Version 3.14159265-2.6-0.999992 (TeX Live 2020/W32TeX)

Bookdown-asetuksissa käytin latex-muunnokseen aluksi pdflatex-valintaa ja vaihdoin sen myöhemmin xelatex-vaihtoehtoon. Ero ei ole merkittävä.

TeX-jakeluna käytin bookdown-paketin kehittäjän suosittelemaa TinyTeX - versiota (https://yihui.org/tinytex/) ja r-pakettia tinytex. Niiden etu on tarvittavien LaTex-pakettien automaattinen asentaminen.

R-ympäristön tarkemmat tiedot:

sessionInfo()

## R version 3.6.3 (2020-02-29)
## Platform: x86_64-w64-mingw32/x64 (64-bit)
## Running under: Windows 10 x64 (build 19041)
## 
## Matrix products: default
## 
## locale:
## [1] LC_COLLATE=English_United Kingdom.1252 
## [2] LC_CTYPE=English_United Kingdom.1252   
## [3] LC_MONETARY=English_United Kingdom.1252
## [4] LC_NUMERIC=C                           
## [5] LC_TIME=English_United Kingdom.1252    
## 
## attached base packages:
## [1] stats     graphics  grDevices utils     datasets  methods   base     
## 
## other attached packages:
##  [1] assertthat_0.2.1  tinytex_0.27      bookdown_0.21     printr_0.1       
##  [5] reshape2_1.4.4    scales_1.1.1      furniture_1.9.7   rmarkdown_2.5    
##  [9] lubridate_1.7.9.2 forcats_0.5.0     stringr_1.4.0     purrr_0.3.4      
## [13] readr_1.4.0       tidyr_1.1.2       tibble_3.0.4      ggplot2_3.3.2    
## [17] tidyverse_1.3.0   knitr_1.30        dplyr_1.0.2       haven_2.3.1      
## [21] ca_0.71.1         rgl_0.100.54     
## 
## loaded via a namespace (and not attached):
##  [1] httr_1.4.2              jsonlite_1.7.1          modelr_0.1.8           
##  [4] shiny_1.5.0             highr_0.8               cellranger_1.1.0       
##  [7] yaml_2.2.1              pillar_1.4.6            backports_1.2.0        
## [10] glue_1.4.2              digest_0.6.27           manipulateWidget_0.10.1
## [13] promises_1.1.1          rvest_0.3.6             colorspace_2.0-0       
## [16] htmltools_0.5.0         httpuv_1.5.4            plyr_1.8.6             
## [19] pkgconfig_2.0.3         broom_0.7.2             xtable_1.8-4           
## [22] webshot_0.5.2           later_1.1.0.1           generics_0.1.0         
## [25] farver_2.0.3            ellipsis_0.3.1          withr_2.3.0            
## [28] cli_2.1.0               magrittr_1.5            crayon_1.3.4           
## [31] readxl_1.3.1            mime_0.9                evaluate_0.14          
## [34] fs_1.5.0                fansi_0.4.1             xml2_1.3.2             
## [37] tools_3.6.3             hms_0.5.3               lifecycle_0.2.0        
## [40] munsell_0.5.0           reprex_0.3.0            compiler_3.6.3         
## [43] rlang_0.4.8             grid_3.6.3              rstudioapi_0.13        
## [46] htmlwidgets_1.5.2       crosstalk_1.1.0.1       miniUI_0.1.1.1         
## [49] labeling_0.4.2          gtable_0.3.0            DBI_1.1.0              
## [52] R6_2.5.0                fastmap_1.0.1           stringi_1.4.6          
## [55] Rcpp_1.0.5              vctrs_0.3.4             dbplyr_2.0.0           
## [58] tidyselect_1.1.0        xfun_0.19

Liite 3: R - koodi

# testaukseen 7.11.2020 virheilmoituksia varten arvo TRUE
options(tinytex.verbose = TRUE)

# 18.10.2020
library(rgl)
library(ca)
library(haven)
library(dplyr)
library(knitr)
library(tidyverse)
library(lubridate)
library(rmarkdown)
library(ggplot2)
library(furniture)
library(scales) # G_1_2 - kuva
library(reshape2)  # G_1_2 - kuva
library(printr) #19.5.18 taulukoiden ja matriisien tulostukseen
library(bookdown)
library(tinytex)
library(assertthat)

# eval = FALSE 24.11.2020
# automatically create a bib database for R packages
knitr::write_bib(c(
  .packages(), 'bookdown', 'knitr', 'rmarkdown'
), 'packages.bib')

# include FALSE: ei koodia eikä tulostusta dokumenttiin - poistettava turhia
# välitulostuksia (18.10.2020)
# Aineiston rajaamisen kolme vaihetta (10.2018)
# 
# TIEDOSTOJEN NIMEÄMINEN
#
# R-datatiedostot .data - tarkenteella ovat osajoukkoja koko ISSP-datasta ISSP2012.data
# R-datatiedostot .dat - tarkenteella: mukana alkuperäisten muuttujien muunnoksia 
# (yleensä as_factor), alkuperäisissä muuttujissa mukana SPSS-tiedoston metadata.
#
# Luokittelumuuttujan tyyppi on datan lukemisen jälkeen yleensä merkkijono (char) 
# ja haven_labelled. 
#
# Muutetaan R-datassa ordinaali- tai  nominaaliasteikon muuttujat haven-paketin 
# as_factor - funktiolla faktoreiksi. R:n faktorityypin muuttujille voidaan tarvittaessa 
# määritellä järjestys, toistaiseksi niin ei tehdä (25.9.2018). 
#
# Muunnetun muuttujan rinnalla säilytetään SPSS-tiedostosta luettu muuttja, metatiedot säilyvät 
# alkuperäisessä.
#       
# R-datatiedostot joiden nimen loppuosa on muotoa *esim1.dat: käytetään analyyseissä
#
# 1. VALITAAN MAAT (25) -> ISSP2012jh1a.data. Muuttujat koodilohkossa datasel_vars1
#
# kolme maa-muuttujaa datassa. V3 erottelee joidenkin maiden alueita, V4 on koko 
# maan koodi ja C_ALPHAN on maan kaksimerkkinen tunnus.
#
# V3 - Country/ Sample ISO 3166 Code (see V4 for codes for whole nation states)
# V3 erot valituissa maissa
# 5601 BE-FLA-Belgium/ Flanders
# 5602 BE-WAL-Belgium/ Wallonia
# 5603 BE-BRU-Belgium/ Brussels
# 27601 DE-W-Germany-West
# 27602 DE-E-Germany-East
# 62001 PT-Portugal 2012: first fieldwork round (main sample)
# 62002 PT-Portugal 2012: second fieldwork round (complementary sample)
# Myös tämä on erikoinen, näyttää olevan vakio kun V4 = 826:
# 82601 GB-GBN-Great Britain
# Portugalissa ainestoa täydennettiin, koska siinä oli puutteita. Jako ei siis ole oleellinen,
# mutta muuut ovat. Tähdellä merkityt maat valitaan johdattelevaan esimerkkiin.
#
# Maat (25)
#
# 36 AU-Australia
# 40 AT-Austria
# 56 BE-Belgium*
# 100 BG-Bulgaria*
# 124 CA-Canada
# 191 HR-Croatia
# 203 CZ-Czech Republic
# 208 DK-Denmark*
# 246 FI-Finland*
# 250 FR-France
# 276 DE-Germany*
# 348 HU-Hungary*
# 352 IS-Iceland
# 372 IE-Ireland
# 428 LV-Latvia
# 440 LT-Lithuania
# 528 NL-Netherlands
# 578 NO-Norway
# 616 PL-Poland
# 620 PT-Portugal
# 643 RU-Russia
# 703 SK-Slovakia
# 705 SI-Slovenia
# 752 SE-Sweden
# 756 CH-Switzerland
# 826 GB-Great Britain and/or United Kingdom - jätetään pois jotta saadaan TOPBOT 
#                          -muuttuja mukaan (top-bottom self-placement) .(9.10.18)
# 840 US-United States - jätetään pois, jotta saadaan TOPBOT-muuttuja mukaan.(10.10.18)
#
# Belgian ja Saksan alueet:
#  V3
#  5601     BE-FLA-Belgium/ Flanders
#  5602     BE-WAL-Belgium/ Wallonia
#  5603     BE-BRU-Belgium/ Brussels
# 27601     DE-W-Germany-West
# 27602     DE-E-Germany-East
#
# Unkari (348) toistaiseksi mukana, mutta joissain kysymyksissä myös Unkarilla on 
# poikkeavia vastausvaihtoehtoja(HU_V18, HU_V19,HU_V20). Jos näitä muuttujia käytetään, 
# Unkari on parempi jättää pois. 
# 
#
# (25.4.2018) user_na  
# haven-paketin read_spss - funktiolla voi r-tiedostoon lukea myös SPSS:n sallimat kolme 
# (yleensä 7, 8, 9) tarkempaa koodia puuttuvalle tiedolle.
# "If TRUE variables with user defined missing will be read into labelled_spss objects. 
# If FALSE, the default, user-defined missings will be converted to NA"
# https://www.rdocumentation.org/packages/haven/versions/1.1.0/topics/read_spss
#
 
ISSP2012jh.data <- read_spss("data/ZA5900_v4-0-0.sav") #luetaan alkuperäinen data R- dataksi (df).

#str(ISSP2012jh.data)

incl_countries25 <- c(36, 40, 56,100, 124, 191, 203, 208, 246, 250, 276, 348, 352, 
                      372, 428, 440, 528, 578, 616, 620, 643, 703, 705, 752, 756)

#str(ISSP2012jh.data)
#str(ISSP2012jh.data) #61754 obs. of  420 variables - kaikki

ISSP2012jh1a.data <- filter(ISSP2012jh.data, V4 %in% incl_countries25)

#head(ISSP2012jh1a.data)
#str(ISSP2012jh1a.data) #34271 obs. of  420 variables, Espanja ja Iso-Britannia
#                       pois (9.10.2018)
# str(ISSP2012jh1a.data) # 32969 obs. of  420 variable, Espanja Iso-Britannia, 
#                        USA pois (10.10.2018)
#
# names() # muuttujen nimet
# Maakohtaiset muuttujat (kun on poikettu ISSP2012 - vastausvaihtoehdoista tms.) 
# on aineistossa eroteltu maatunnus-etuliitteellä (esimerkiksi ES_V7).
# Demografisissa ja muissa taustamuuttujissa suuri osa tiedoista on kerätty maa-
# kohtaisilla lomakkeilla. Vertailukelpoiset muuttujat on konstruoitu niistä.
# Muuttujia on 420, vain osa yhteisiä kaikille maille.

# include FALSE: ei koodia eikä tulostusta dokumenttiin - poistettava turhia
# välitulostuksia (18.10.2020)
# 2. VALITAAN MUUTTUJAT  -> ISSP2012jh1b.data. Maat valittu koodilohkossa datasel_country1
#
#
# Muuttujat on luokiteltu dokumentissa ZA5900_overview.pdf
# https://zacat.gesis.org/webview/index.jsp?object=http://zacat.gesis.org/obj/fStudy/ZA5900
# Study Description -> Other Study Description -> Related Materials
# 
#

# METADATA

metavars1 <- c("V1", "V2", "DOI")

#MAA - maakoodit ja maan kahden merkin tunnus

countryvars1 <- c("V3","V4","C_ALPHAN")

# SUBSTANSSIMUUTTUJAT - Attitudes towards family and gender roles (9)
#
# Yhdeksän kysymystä (lyhennetyt versiot, englanniksi), vastausvaihtoehdot Q1-Q2
#
# 1 = täysin samaa mieltä, 2 = samaa mieltä, 3 = ei samaa eikä eri mieltä, 
# 4 = eri mieltä, 5 = täysin eri mieltä
# 
# Q1a Working mother can have warm relation with child
# Q1b Pre-school child suffers through working mother
# Q1c Family life suffers through working mother
# Q1d Women’s preference: home and children
# Q1e Being housewife is satisfying
#
# Q2a Both should contribute to household income
# Q2b Men’s job is earn money, women’s job household
#
# Q3a Should women work: Child under school age 
# Q3b Should women work: Youngest kid at school
# 1= kokopäivätyö, 2 = osa-aikatyö, 3 = pysyä kotona, 8 = en osaa sanoa
# (can't choose), 9 = no answer
#
# Kysymysten Q3a ja Q3b eos-vastaus ei ole sama kuin "en samaa enkä eri  mieltä"
# (ns. neutraali # vaihtoehto), mutta kieltäytymisiä jne. (koodi 9) on aika
# vähän. Kolmessa # maassa ne on yhdistety: 
# (8 Can't choose, CA:can't choose+no answer, KR:don't know+refused, NL:don't know).
# Kun SPSS-tiedostosta ei ole tuotu puuttuvan tiedon tarkempaa luokittelua,
# erottelua ei voi tehdä.
#

substvars1 <- c("V5","V6","V7","V8","V9","V10","V11","V12","V13") # 9 muuttujaa

# Nämä yhteiset muuttujat pois (maaspesifien muuttujien lisäksi) :
#
# "V14","V15","V16",  "V17","V18","HU_V18","V19","HU_V19","V20","HU_V20","V21",
# "V28","V29","V30","V31","V32","V33",# "V34", "V35", "V36", "V37", "V38", "V39",
# "V40", "V41", "V42", "V43", "V44", "V45", "V46", "V47", "V48", "V49", "V50", 
# "V51", "V52", "V53", "V54", "V55", "V56", "V57", "V58", "V59", "V60", "V61", 
# "V62", "V63", "V64", "V65", "V65a","V66", "V67"
#
#
# DEMOGRAFISET JA MUUT TAUSTAMUUTTUJAT (8)
#
# AGE, SEX
#
# DEGREE - Highest completed degree of education: Categories for international
# comparison. Slightly re-arranged subset of ISCED-97
#
# 0 No formal education
# 1 Primary school (elementary school)
# 2 Lower secondary (secondary completed does not allow entry to university:
#  obligatory school)
# 3 Upper secondary (programs that allow entry to university or programs that
#  allow to entry other ISCED level 3 programs - designed to prepare students for
#  direct entry into the labour market)
# 4 Post secondary, non-tertiary (other upper secondary programs toward labour
#  market or technical formation)
# 5 Lower level tertiary, first stage (also technical schools at a tertiary level)
# 6 Upper level tertiary (Master, Dr.)
# 9 No answer, CH: don't know
# HUOM! R-factor - muunnoksessa koodaus on 1-7
#
# MAINSTAT - main status: Which of the following best describes your current situation?
#
# 1 In paid work
# 2 Unemployed and looking for a job, HR: incl never had a job
# 3 In education
# 4 Apprentice or trainee
# 5 Permanently sick or disabled
# 6 Retired
# 7 Domestic work
# 8 In compulsory military service or community service
# 9 Other
# 99 No answer
# Armeijassa tai yhdyskuntapalvelussa muutamia, muutamissa maissa.Kategoriassa 9 
# on hieman väkeä. Yhdistetään 8 ja 9. Huom! Esim Puolassa ei yhtään eläkeläistä
# eikä kategoriaa 9, Saksassa ei ketään kategoriassa 9.
#
# TOPBOT - Top-Bottom self-placement (10 pt scale)
#
# "In our society, there are groups which tend to be towards the top and groups 
# which tend to be towards the bottom. Below is a scale that runs
# from the top to the bottom. Where would you put yourself on this scale?"
# Eri maissa hieman erilaisia kysymyksiä. 
#
# HHCHILDR - How many children in household: children between [school age] and
# 17 years of age
#
# 0 No children
# 1 One child
# 2 2 children
# 21 21 children
# 96 NAP (Code 0 in HOMPOP)
# 97 Refused
# 99 No answer
#
# Voisi koodata dummymuuttujaksi lapsia (1) - ei lapsia (0).
# Ranskan datassa on erittäin iso osa puuttuvia tietoja (yli 20 %), Sama tilanne
# myös  muissa perheen kokoon liittyvissä kysymyksissä.  Myös Austarlialla aika
# paljon puuttuvia vastauksia.
#
# MARITAL - Legal partnership status 
#
# What is your current legal marital status?
# The aim of this variable is to measure the current 'legal' marital status '. 
# PARTLIV - muuttujassa on 'de facto' - tilanteen tieto parisuhteesta
#
# 1 Married
# 2 Civil partnership
# 3 Separated from spouse/ civil partner (still legally married/ still legally 
#   in a civil partnership)
# 4 Divorced from spouse/ legally separated from civil partner
# 5 Widowed/ civil partner died
# 6 Never married/ never in a civil partnership, single
# 7 Refused
# 8 Don't know
# 9 No answer
#
# URBRURAL - Place of living: urban - rural
#
# 1 A big city
# 2 The suburbs or outskirts of a big city
# 3 A town or a small city
# 4 A country village
# 5 A farm or home in the country
# 7 Other answer
# 9 No answer
# 1 ja 2 vaihtelevat aika paljon maittain, parempi laskea yhteen. Unkarista puuttuu 
# jostain syystä kokonaan vaihtoehto 5.  Vaihotehdon 7 on valinnut vain 4
# vastaajaa Ranskasta.
#

bgvars1 <- c( "SEX","AGE","DEGREE", "MAINSTAT", "TOPBOT",
              "HHCHILDR", "MARITAL", "URBRURAL")

#Valitaan muuttujat

jhvars1 <- c(metavars1,countryvars1, substvars1,bgvars1)

#jhvars1
ISSP2012jh1b.data <- select(ISSP2012jh1a.data, all_of(jhvars1)) 

# laaja aineisto - mukana havainnot joissa puuttuvia tietoja
# str(ISSP2012jh1b.data) #32969 obs. of  23 variables 
# 
# SUBSTANSSIMUUTTUJAT
#
# $ V5      : 'haven_labelled' num  5 1 2 2 1 NA 2 4 2 2 ...
#  ..- attr(*, "label")= chr "Q1a Working mom: warm relationship with children
#       as a not working mom"
#  ..- attr(*, "labels")= Named num  0 1 2 3 4 5 8 9
#
# ISSP2012jh1b.data$V5 näyttää tarkemmin rakenteen
#
# glimpse(ISSP2012jh1b.data)

# Poistetaan havainnot, joissa ikä (AGE) tai sukupuolitieto puuttuu (5.7.2019)

ISSP2012jh1c.data <- filter(ISSP2012jh1b.data, (!is.na(SEX) & !is.na(AGE)))

# str(ISSP2012jh1c.data) # 32823 obs. of  23 variables, 32969-32823 = 146
# TARKISTUS 8.6.20 dplyr 1.0.0-päivitys: havaintojen ja muuttujien määrä ok.

# VAIHE 1 - muuttujat joissa ei ole puuttuvia tietoja

# vaihe 1.1 haven_labelled ja chr -> as_factor

ISSP2012jh1d.dat <- ISSP2012jh1c.data %>%
    mutate(maa = as_factor(C_ALPHAN), # ei puuttuvia, ei tyhjiä leveleitä
           maa3 = as_factor(V3),  # maakoodi, jossa aluejako joillan mailla
           sp1 = as_factor(SEX), # ei puuttuvia, tyhjä level "no answer" 999
         )


# C_ALPHAN - maa - maa3 tarkistuksia

# V3
# "Pulma" on järjestys. C_ALPHAN ("chr") on aakkosjärjestyksessä, kun luodaan
# maa = as_factor(C_ALPHAN) järjestys muuttuu (esiintymisjärjestys datassa?)
# maa3 muunnetaan maakoodista (haven_labelled' num), jonka

# str(ISSP2012jh1d.dat$maa) #Country Prefix ISO 3166 Code - alphanumeric
# attributes(ISSP2012jh1d.dat$maa) # ei tyhiä levels-arvoja, 25 levels
# ISSP2012jh1d.dat$maa %>% fct_unique()
# ISSP2012jh1d.dat$maa %>% fct_count() # summary kertoo samat tiedot (20.2.20)
# sum(is.na(ISSP2012jh1d.dat$maa)) # ei puuttuvia tietoja
# ISSP2012jh1d.dat$maa %>% summary() # mukana vain valitut 25 maata

# str(ISSP2012jh1d.dat$maa3)  #"Country/ Sample ISO 3166 Code
                            #(see V4 for codes for whole nation states)"
                            # 29 levels
# str(ISSP2012jh1d.dat$V3)

# attributes(ISSP2012jh1d.dat$maa3) # ei tyhiä levels-arvoja, 29 levels
# sum(is.na(ISSP2012jh1d.dat$maa3)) # nolla ei ole puuttuva tieto! (3.2.20)
# ISSP2012jh1d.dat$maa3 %>% fct_unique()
# ISSP2012jh1d.dat$maa3 %>% fct_count()
# Vain näissä on jaettu maan havainnot (3.2.20)
#
# [38] BE-FLA-Belgium/ Flanders
# [39] BE-WAL-Belgium/ Wallonia
# [40] BE-BRU-Belgium/ Brussels
# [41] DE-W-Germany-West
# [42] DE-E-Germany-East
# [43] PT-Portugal 2012: first fieldwork round (main sample)
# [44] PT-Portugal 2012: second fieldwork round (complementary sample)

# ISSP2012jh1d.dat$maa3 %>% fct_count() #miksi ei tulosta mitään? (3.2.2020)

# ISSP2012jh1d.dat$maa3 %>% summary()
# ISSP2012jh1d.dat$maa3 %>% fct_unique()
# maa3: 25 maata, havaintojen määrä. Poisjätetyissä havaintoja 0.
# glimpse(ISSP2012jh1d.dat$maa3)
# head(ISSP2012jh1d.dat$maa3)
# length(levels(ISSP2012jh1d.dat$maa3))

# C_ALPHAN alkuperäinen järjestys, maa aakkosjärjestyssä  (2.2.20)
#
# Huom1: Myös merkkijonomuuttujaa C_ALPHAN tarvitaan jatkossa.
#
# Huom2: kun dataa rajataan, on tarkistettava ja tarvittaessa poistettava
# "tyhjät" R-factor - muuttujan "maa" luokat (3.2.2020)


# vaihe 1.2 tyhjät luokat (levels) pois faktoreista

ISSP2012jh1d.dat <- ISSP2012jh1d.dat %>%
    mutate(sp = fct_drop(sp1),
           maa3 = fct_drop(maa3)
           )

#  maa3 - tarkistuksia

# str(ISSP2012jh1d.dat$maa3)  # 29 levels
# attributes(ISSP2012jh1d.dat$maa3)
#sum(is.na(ISSP2012jh1d.dat$maa3)) # nolla ei ole puuttuva tieto! (3.2.20)
# ISSP2012jh1d.dat$maa3 %>% summary()
# ISSP2012jh1d.dat$maa3 %>% fct_unique()
# ISSP2012jh1d.dat$maa3 %>% fct_count()
#
# str(ISSP2012jh1d.dat$C_ALPHAN)
# attributes(ISSP2012jh1d.dat$C_ALPHAN)

# TESTAUKSIA
# 
# ISSP2012jh1d.dat %>% tableX(C_ALPHAN, maa)
# ISSP2012jh1d.dat %>% tableX(C_ALPHAN, maa3)
# ISSP2012jh1d.dat %>% tableX(maa, maa3)
# ISSP2012jh1d.dat %>% tableX(V3, maa3)

# sp, sp1, SEX - tarkistuksia
# 
# ISSP2012jh1d.dat$sp %>% fct_count()
# ISSP2012jh1d.dat$sp %>% fct_count()
# ISSP2012jh1d.dat %>% tableX(SEX,sp1)
# ISSP2012jh1d.dat %>% tableX(SEX,sp)
# ISSP2012jh1d.dat %>% tableX(sp1,sp)

# vaihe 1.3 uudet "faktorilabelit"
ISSP2012jh1d.dat <- ISSP2012jh1d.dat %>%
    mutate(sp =
          fct_recode(sp,
            "m" = "Male",
            "f" = "Female")
            )

# Tarkistuksia

# ISSP2012jh1d.dat$sp %>% fct_unique()
# ISSP2012jh1d.dat$sp %>% fct_count()
# ISSP2012jh1d.dat$sp %>% summary()

# AGE -> ika
ISSP2012jh1d.dat$ika <- ISSP2012jh1d.dat$AGE

# Tarkistuksia
attributes(ISSP2012jh1d.dat$ika) # tyhjä level "No answer"
# str(ISSP2012jh1d.dat$ika)
ISSP2012jh1d.dat$ika %>% summary()

ISSP2012jh1d.dat %>%
tableC(AGE, ika,cor_type = "pearson", na.rm = FALSE, rounding = 5,
       output = "text", booktabs = TRUE, caption = NULL, align = NULL,
       float = "htb") %>% kable()

# Ikäjakauma - ei tarvita (18.10.2020)
#
# ISSP2012jh1d.dat$ika %>% hist(main = "ISSP 2012: vastaajan ikä")

# Substanssi- ja taustamuuttujat R-faktoreiksi
ISSP2012jh1d.dat <- ISSP2012jh1d.dat %>%
    mutate(Q1a1 = as_factor(V5), #labels
            Q1b1 = as_factor(V6),
            Q1c1 = as_factor(V7),
            Q1d1 = as_factor(V8),
            Q1e1 = as_factor(V9),
            Q2a1 = as_factor(V10),
            Q2b1 = as_factor(V11),
            Q3a1 = as_factor(V12), #labels = vastQ3_labels (W,w,H)
            Q3b1 = as_factor(V13), #labels = vastQ3_labels
            edu1 = as_factor(DEGREE),
            msta1 = as_factor(MAINSTAT),
            sosta1 = as_factor(TOPBOT),
            nchild1 = as_factor(HHCHILDR),
            lifsta1 = as_factor(MARITAL),
            urbru1 = as_factor(URBRURAL)
           )

# Muuttujat Q1a1...urbru1 ovat apumuuttujia, joissa on periaatteessa kaikki SPSS-
# tiedostosta siirtyvä metatieto. Poikkeus on SPSS:n kolme tarkentavaa koodia
# puuttuvalle tiedolle, ne saisi mukaan read_spss - parametrin avulla (user_na=TRUE)
#

# Tarkistusksia
# ISSP2012jh1d.dat %>% summary()

# ISSP2012jh1d.dat %>%
#    select(Q1a1, Q1b1, Q1c1,Q1d1,Q1e1, Q2a1, Q2b1, Q3a1,Q3b1) %>%
#    summary()
#
# ISSP2012jh1d.dat %>%
#    select(edu1,msta1, sosta1, nchild1, lifsta1, urbru1) %>%
#    summary()


# Substanssimuuttujat - ristiintaulukoinnit riittävät (6.2.20)

# ISSP2012jh1d.dat$Q1a1 %>% fct_count()
# ISSP2012jh1d.dat$Q1b1 %>% fct_count()
# ISSP2012jh1d.dat$Q1c1 %>% fct_count()
# ISSP2012jh1d.dat$Q1d1 %>% fct_count()
# ISSP2012jh1d.dat$Q1e1 %>% fct_count()
# ISSP2012jh1d.dat$Q2a1 %>% fct_count()
# ISSP2012jh1d.dat$Q2b1 %>% fct_count()
# ISSP2012jh1d.dat$Q3a1 %>% fct_count()
#ISSP2012jh1d.dat$Q3b1 %>% fct_count()

# Taustamuuttujat - ristiintaulukoinnit riittävät (6.2.20)

# ISSP2012jh1d.dat$edu1 %>% fct_count()
# ISSP2012jh1d.dat$msta1 %>% fct_count()
# ISSP2012jh1d.dat$sosta1 %>% fct_count()
# ISSP2012jh1d.dat$nchild1 %>% fct_count()
# ISSP2012jh1d.dat$lifsta1 %>% fct_count()
# ISSP2012jh1d.dat$urbru1 %>% fct_count()

# Poistetaan tyhjät luokat muuttujista

ISSP2012jh1d.dat <- ISSP2012jh1d.dat %>%
    mutate(Q1a = fct_drop(Q1a1),
           Q1b = fct_drop(Q1b1),
           Q1c = fct_drop(Q1c1),
           Q1d = fct_drop(Q1d1),
           Q1e = fct_drop(Q1e1),
           Q2a = fct_drop(Q2a1),
           Q2b = fct_drop(Q2b1),
           Q3a = fct_drop(Q3a1),
           Q3b = fct_drop(Q3b1),
           edu = fct_drop(edu1),
           msta = fct_drop(msta1),
           sosta = fct_drop(sosta1),
           nchild = fct_drop(nchild1),
           lifsta = fct_drop(lifsta1),
           urbru = fct_drop(urbru1)

    )
# Tarkistuksia 1

# ISSP2012jh1d.dat %>% summary()
# ISSP2012jh1d.dat %>%
#    select(Q1a, Q1b, Q1c, Q1d, Q1e,Q2a,Q2b,Q3a, Q3b) %>%
#    str()
#ISSP2012jh1d.dat %>%
#    select(Q1a1, Q1b1, Q1c1, Q1d1, Q1e1,Q2a1,Q2b1,Q3a1, Q3b1) %>%
#    str()
#ISSP2012jh1d.dat %>%
#    select(edu, msta, sosta, nchild,lifsta, urbru) %>%
#    str()
#ISSP2012jh1d.dat %>%
#    select(edu1, msta1, sosta1, nchild1,lifsta1, urbru1) %>%
#    str()

# Tarkistuksia 2 - ristiintaulukointeja
# Substanssimuuttujat

# ISSP2012jh1d.dat %>% tableX(Q1a,Q1a1)
# ISSP2012jh1d.dat %>% tableX(Q1b,Q1b1)
# ISSP2012jh1d.dat %>% tableX(Q1c,Q1c1)
# ISSP2012jh1d.dat %>% tableX(Q1d,Q1d1)
# ISSP2012jh1d.dat %>% tableX(Q1e,Q1e1)
# ISSP2012jh1d.dat %>% tableX(Q2a,Q2a1)
# ISSP2012jh1d.dat %>% tableX(Q2b,Q2b1)
# ISSP2012jh1d.dat %>% tableX(Q3a,Q3a1)
# ISSP2012jh1d.dat %>% tableX(Q3b,Q3b1)

# Taustamuuttujat

# ISSP2012jh1d.dat %>% tableX(edu,edu1)
# ISSP2012jh1d.dat %>% tableX(msta,msta1)
# ISSP2012jh1d.dat %>% tableX(sosta,sosta1)
# ISSP2012jh1d.dat %>% tableX(nchild,nchild1)
# ISSP2012jh1d.dat %>% tableX(lifsta,lifsta1)
# ISSP2012jh1d.dat %>% tableX(urbru,urbru1)

# Uusi muuttuja, jossa NA-arvot ovat mukana muuttujan uutena luokkana. Muuttujat
# nimetään Q1a -> Q1am.

ISSP2012jh1d.dat <- ISSP2012jh1d.dat %>%
    mutate(Q1am = fct_explicit_na(Q1a, na_level = "missing"),
           Q1bm = fct_explicit_na(Q1b, na_level = "missing"),
           Q1cm = fct_explicit_na(Q1c, na_level = "missing"),
           Q1dm = fct_explicit_na(Q1d, na_level = "missing"),
           Q1em = fct_explicit_na(Q1e, na_level = "missing"),
           Q2am = fct_explicit_na(Q2a, na_level = "missing"),
           Q2bm = fct_explicit_na(Q2b, na_level = "missing"),
           Q3am = fct_explicit_na(Q3a, na_level = "missing"),
           Q3bm = fct_explicit_na(Q3b, na_level = "missing"),
           edum = fct_explicit_na(edu, na_level = "missing"),
           mstam = fct_explicit_na(msta, na_level = "missing"),
           sostam = fct_explicit_na(sosta, na_level = "missing"),
           nchildm = fct_explicit_na(nchild, na_level = "missing"),
           lifstam = fct_explicit_na(lifsta, na_level = "missing"),
           urbrum = fct_explicit_na(urbru, na_level = "missing"),
           )
# Tarkistuksia 3

# ISSP2012jh1d.dat %>%
#    select(Q1am, Q1bm, Q1cm, Q1dm, Q1em, Q2am, Q2bm, Q3am, Q3bm) %>%
#    summary()
#
#ISSP2012jh1d.dat %>%
#    select(edum,mstam, sostam,nchildm,lifstam, urbrum) %>%
#    summary()
#
#ISSP2012jh1d.dat %>%
#    select(Q1am, Q1bm, Q1cm, Q1dm, Q1em, Q2am, Q2bm, Q3am, Q3bm) %>%
#    str()
#
#ISSP2012jh1d.dat %>%
#    select(edum,mstam, sostam,nchildm,lifstam, urbrum) %>%
#    str()

# Taustamuuttuja, puuttuva tieto mukana - ristiintaulkointeja

# ISSP2012jh1d.dat$edum %>% fct_count()
# ISSP2012jh1d.dat$mstam %>% fct_count()
# ISSP2012jh1d.dat$sostam %>% fct_count()
# ISSP2012jh1d.dat$nchildm %>% fct_count()
# ISSP2012jh1d.dat$lifstam %>% fct_count()
# ISSP2012jh1d.dat$urbrum %>% fct_count()

# Substanssimuuttujat, puuttuva tieto mukana  - ristiintaulkointeja

# ISSP2012jh1d.dat$Q1am %>% fct_count()
# ISSP2012jh1d.dat$Q1bm %>% fct_count()
# ISSP2012jh1d.dat$Q1cm %>% fct_count()
# ISSP2012jh1d.dat$Q1dm %>% fct_count()
# ISSP2012jh1d.dat$Q1em %>% fct_count()
# ISSP2012jh1d.dat$Q2am %>% fct_count()
# ISSP2012jh1d.dat$Q2bm %>% fct_count()
# ISSP2012jh1d.dat$Q3am %>% fct_count()
# ISSP2012jh1d.dat$Q3bm %>% fct_count()

# Vaihe 2.4.1

# Q1a - Q1e,Q2a, Q2b  Viisi vastausvaihtoehtoa - ei eksplisiittistä NA-tietoa("missing")
# Q3a - Q3b  kolme vastausvaihtoehtoa

ISSP2012jh1d.dat <- ISSP2012jh1d.dat %>%
    mutate(Q1a = fct_recode(Q1a,
                        "S" = "Strongly agree",
                        "s" = "Agree",
                        "?" = "Neither agree nor disagree",
                        "e" = "Disagree",
                        "E"= "Strongly disagree"),
            Q1b = fct_recode(Q1b,
                      "S" = "Strongly agree",
                      "s" = "Agree",
                      "?" = "Neither agree nor disagree",
                      "e" = "Disagree",
                      "E" = "Strongly disagree"),
           Q1c = fct_recode(Q1c,
                           "S" = "Strongly agree",
                           "s" = "Agree",
                           "?" = "Neither agree nor disagree",
                           "e" = "Disagree",
                           "E" = "Strongly disagree"),
           Q1d = fct_recode(Q1d,
                           "S" = "Strongly agree",
                           "s" = "Agree",
                           "?" = "Neither agree nor disagree",
                           "e" = "Disagree",
                           "E" = "Strongly disagree"),
           Q1e = fct_recode(Q1e,
                           "S" = "Strongly agree",
                           "s" = "Agree",
                           "?" = "Neither agree nor disagree",
                           "e" = "Disagree",
                           "E" = "Strongly disagree"),
          Q2a = fct_recode(Q2a,
                           "S" = "Strongly agree",
                           "s" = "Agree",
                           "?" = "Neither agree nor disagree",
                           "e" = "Disagree",
                           "E" = "Strongly disagree" ),
          Q2b = fct_recode(Q2b,
                           "S" = "Strongly agree",
                           "s" = "Agree",
                           "?" = "Neither agree nor disagree",
                           "e" = "Disagree",
                           "E" = "Strongly disagree"),
          Q3a = fct_recode(Q3a,
                          "W" = "Work full-time",
                          "w" = "Work part-time",
                          "H" = "Stay at home" ),
          Q3b = fct_recode(Q3b,
                           "W" = "Work full-time",
                           "w" = "Work part-time",
                           "H" = "Stay at home" )
                        )


# Tarkistuksia 1
# ISSP2012jh1d.dat %>%
#    select(Q1a, Q1b, Q1c, Q1d, Q1e, Q2a, Q2b, Q3a, Q3b) %>%
#    summary()


# Vaihe 2.4.2 - muuttujassa eksplisiittinen NA-tieto
ISSP2012jh1d.dat <- ISSP2012jh1d.dat %>%
    mutate(Q1am = fct_recode(Q1am,
                            "S" = "Strongly agree",
                            "s" = "Agree",
                            "?" = "Neither agree nor disagree",
                            "e" = "Disagree",
                            "E" = "Strongly disagree",
                            "P" = "missing"),
           Q1bm = fct_recode(Q1bm,
                           "S" = "Strongly agree",
                           "s" = "Agree",
                           "?" = "Neither agree nor disagree",
                           "e" = "Disagree",
                           "E" = "Strongly disagree",
                           "P" = "missing"),
           Q1cm = fct_recode(Q1cm,
                           "S" = "Strongly agree",
                           "s" = "Agree",
                           "?" = "Neither agree nor disagree",
                           "e" = "Disagree",
                           "E" = "Strongly disagree",
                           "P" = "missing"),
           Q1dm = fct_recode(Q1dm,
                           "S" = "Strongly agree",
                           "s" = "Agree",
                           "?" = "Neither agree nor disagree",
                           "e" = "Disagree",
                           "E" = "Strongly disagree",
                           "P" = "missing"),
           Q1em = fct_recode(Q1em,
                           "S" = "Strongly agree",
                           "s" = "Agree",
                           "?" = "Neither agree nor disagree",
                           "e" = "Disagree",
                           "E" = "Strongly disagree",
                           "P" = "missing"),
           Q2am = fct_recode(Q2am,
                            "S" = "Strongly agree",
                            "s" = "Agree",
                            "?" = "Neither agree nor disagree",
                            "e" = "Disagree",
                            "E" = "Strongly disagree",
                            "P" = "missing"),
           Q2bm = fct_recode(Q2bm,
                            "S" = "Strongly agree",
                            "s" = "Agree",
                            "?" = "Neither agree nor disagree",
                            "e" = "Disagree",
                            "E" = "Strongly disagree",
                            "P" = "missing"),
           Q3am = fct_recode(Q3am,
                            "W" = "Work full-time",
                            "w" = "Work part-time",
                            "H" = "Stay at home",
                            "P" = "missing"),
           Q3bm = fct_recode(Q3bm,
                            "W" = "Work full-time",
                            "w" = "Work part-time",
                            "H" = "Stay at home",
                            "P" = "missing")
               )

# Tarkistuksia 4

# ISSP2012jh1d.dat %>%
#    select(Q1am, Q1bm, Q1cm, Q1dm, Q1em, Q2am, Q2bm, Q3am, Q3bm) %>%
#    summary()

# Tarkistuksia 5

# Substanssimuuttuja

# ISSP2012jh1d.dat %>%
#    tableX(Q1a,Q1am)
#
# ISSP2012jh1d.dat %>%
#    tableX(Q1b,Q1bm)
#
# ISSP2012jh1d.dat %>%
#    tableX(Q1c,Q1cm)
#
# ISSP2012jh1d.dat %>%
#    tableX(Q1d,Q1dm)
#
# ISSP2012jh1d.dat %>%
#    tableX(Q1e,Q1em)
#
# ISSP2012jh1d.dat %>%
#    tableX(Q2a,Q2am)
#
# ISSP2012jh1d.dat %>%
#    tableX(Q2b,Q2bm)
#
# ISSP2012jh1d.dat %>%
#    tableX(Q3a,Q3am)
#
# ISSP2012jh1d.dat %>%
#    tableX(Q3b,Q3bm)
#
# ISSP2012jh1d.dat %>% 
#    tableX(Q3am,Q3a)
#
# ISSP2012jh1d.dat$Q3a %>% levels()
# ISSP2012jh1d.dat$Q3am %>% levels()

# Taustamuuttujat - ristiintaulukointeja

# ISSP2012jh1d.dat %>%
#    tableX(edu, edum)
# ISSP2012jh1d.dat %>%
#    tableX(msta, mstam)
# ISSP2012jh1d.dat %>%
#    tableX(sosta, sostam)
# ISSP2012jh1d.dat %>%
#    tableX(nchild,nchildm)
# ISSP2012jh1d.dat %>%
#    tableX(lifsta, lifstam)
# ISSP2012jh1d.dat %>%
#    tableX(urbru, urbrum)

# (16.9.2020) Testaus uusille muuttujille
# Koodilohkoissa on jo testattu taulukoimalla muuttujia. Tässä varmistetaan, että
# muuttujat pysyvät sellaisina millaisiksi ne on luotu.

# ika - onpas hankala testata !
# Min. 1st Qu.  Median    Mean 3rd Qu.    Max.
# 15.00   36.00   50.00   49.52   63.00  102.00
# ikatest <- ISSP2012jh1d.dat$ika %>% summary()
#   ikatest <- ikatest[2,]
#validate_that(are_equal(ikatest, c(15, 36, 50, 49.5, 63, 102)))
#str(ISSP2012jh1d.dat)
#ISSP2012jh1d.dat %>% 

# substanssimuuttujat 1
# Q1a, Q1b, Q1c, Q1d, Q1e, Q2a, Q2b, Q3a, Q3b (r. 423->)

validate_that(length(levels(ISSP2012jh1d.dat$Q1a)) == 5)
validate_that(are_equal(levels(ISSP2012jh1d.dat$Q1a),
               c("S", "s", "?", "e", "E")))
validate_that(length(levels(ISSP2012jh1d.dat$Q1b)) == 5)
validate_that(are_equal(levels(ISSP2012jh1d.dat$Q1b),
               c("S", "s", "?", "e", "E")))
validate_that(length(levels(ISSP2012jh1d.dat$Q1c)) == 5)
validate_that(are_equal(levels(ISSP2012jh1d.dat$Q1c),
               c("S", "s", "?", "e", "E")))
validate_that(length(levels(ISSP2012jh1d.dat$Q1d)) == 5)
validate_that(are_equal(levels(ISSP2012jh1d.dat$Q1d),
               c("S", "s", "?", "e", "E")))
validate_that(length(levels(ISSP2012jh1d.dat$Q1e)) == 5)
validate_that(are_equal(levels(ISSP2012jh1d.dat$Q1e),
               c("S", "s", "?", "e", "E")))
validate_that(length(levels(ISSP2012jh1d.dat$Q2a)) == 5)
validate_that(are_equal(levels(ISSP2012jh1d.dat$Q2a),
               c("S", "s", "?", "e", "E")))
validate_that(length(levels(ISSP2012jh1d.dat$Q2b)) == 5)
validate_that(are_equal(levels(ISSP2012jh1d.dat$Q2b),
               c("S", "s", "?", "e", "E")))

# substanssimuuttujat 2

validate_that(length(levels(ISSP2012jh1d.dat$Q3a)) == 3)
validate_that(are_equal(levels(ISSP2012jh1d.dat$Q3a),
               c("W", "w", "H")))
validate_that(length(levels(ISSP2012jh1d.dat$Q3b)) == 3)
validate_that(are_equal(levels(ISSP2012jh1d.dat$Q3b),
               c("W", "w", "H")))



# substanssimuuttujat, puuttuva tieto muuttujan arvona
# Q1am, Q1bm, Q1cm, Q1dm, Q1em, Q2am, Q2bm, Q3am, Q3bm

validate_that(length(levels(ISSP2012jh1d.dat$Q1am)) == 6)
validate_that(are_equal(levels(ISSP2012jh1d.dat$Q1am),
               c("S", "s", "?", "e", "E", "P")))
validate_that(length(levels(ISSP2012jh1d.dat$Q1bm)) == 6)
validate_that(are_equal(levels(ISSP2012jh1d.dat$Q1bm),
               c("S", "s", "?", "e", "E", "P")))
validate_that(length(levels(ISSP2012jh1d.dat$Q1cm)) == 6)
validate_that(are_equal(levels(ISSP2012jh1d.dat$Q1cm),
               c("S", "s", "?", "e", "E", "P")))
validate_that(length(levels(ISSP2012jh1d.dat$Q1dm)) == 6)
validate_that(are_equal(levels(ISSP2012jh1d.dat$Q1dm),
               c("S", "s", "?", "e", "E", "P")))
validate_that(length(levels(ISSP2012jh1d.dat$Q1em)) == 6)
validate_that(are_equal(levels(ISSP2012jh1d.dat$Q1em),
               c("S", "s", "?", "e", "E", "P")))
validate_that(length(levels(ISSP2012jh1d.dat$Q2am)) == 6)
validate_that(are_equal(levels(ISSP2012jh1d.dat$Q2am),
               c("S", "s", "?", "e", "E", "P")))
validate_that(length(levels(ISSP2012jh1d.dat$Q2bm)) == 6)
validate_that(are_equal(levels(ISSP2012jh1d.dat$Q2bm),
               c("S", "s", "?", "e", "E", "P")))

validate_that(length(levels(ISSP2012jh1d.dat$Q3am)) == 4)
validate_that(are_equal(levels(ISSP2012jh1d.dat$Q3am),
               c("W", "w", "H", "P")))
validate_that(length(levels(ISSP2012jh1d.dat$Q3bm)) == 4)
validate_that(are_equal(levels(ISSP2012jh1d.dat$Q3bm),
               c("W", "w", "H", "P")))

# taustamuuttujat puuttuvilla tiedoilla ja ilman
# testataan vain tasojen määrä, ei labeleita jotka ovat 
# alkuperäisestä datasta.

# edu, edum Huom! Koulutustasoluokitus alkuperäisessä
# datassa 0-6 (ei muodollista koulusta - korkeampi kolmas aste (maisteri, tohtori)
# R-faktorissa 1-7

validate_that(length(levels(ISSP2012jh1d.dat$edu)) == 7)
validate_that(length(levels(ISSP2012jh1d.dat$edum)) == 8)

# msta, mstam
validate_that(length(levels(ISSP2012jh1d.dat$msta)) == 9)
validate_that(length(levels(ISSP2012jh1d.dat$mstam)) == 10)

# sosta, sostam
validate_that(length(levels(ISSP2012jh1d.dat$sosta)) == 10)
validate_that(length(levels(ISSP2012jh1d.dat$sostam)) == 11)

# nchild, ncildm
validate_that(length(levels(ISSP2012jh1d.dat$nchild)) == 11)
validate_that(length(levels(ISSP2012jh1d.dat$nchildm)) == 12)

# lifsta, lifstam
validate_that(length(levels(ISSP2012jh1d.dat$lifsta)) == 6)
validate_that(length(levels(ISSP2012jh1d.dat$lifstam)) == 7)

# urbru, urbrum
validate_that(length(levels(ISSP2012jh1d.dat$urbru)) == 5)
validate_that(length(levels(ISSP2012jh1d.dat$urbrum)) == 6)

issp_docname <- c("Variable Report", "Study Monitoring Report","Basic Questionnaire",
                  "Contents of ISSP 2012 module", "Questionnaire Development")
issp_docdesc <- c("Perusdokumentti, muuttujien kuvaukset ja taulukot",
                  "tiedokeruun toteutus eri maissa",
                  "Maittain sovellettava kyselylomake", "substanssikysymykset taulukkona",
                  "kyselylomakkeen laatiminen")
issp_docfile <- c("ZA5900_cdb.pdf", "ZA5900_mr.pdf", "ZA5900_bq.pdf","ZA5900_overview.pdf",
                  "ssoar-2014-scholz_et_al-ISSP_2012_Family_and_Changing.pdf")


col_isspdocs <- c("dokumentti","sisältö","tiedosto")

ISSPdocsT.tbl <- tibble(issp_docname, issp_docdesc, issp_docfile)
colnames(ISSPdocsT.tbl) <- col_isspdocs

knitr::kable(ISSPdocsT.tbl, booktab = TRUE,
             caption = ' ISSP 2012: tärkeimmät dokumentit')


# Muuttuja taulukkona - karkea tapa
# HUOM! Taulkot ovat hankalia, kun tulostus halutaan pdf- ja html- formaattiin
# Kysymyste pitkät versiot on siksi esitetty suomenkielisen lomakkeen kuvana.

tabVarnames <- c(substvars1,bgvars1) # muuttujanimet muuttujille

# Kysymysten lyhyet versiot englanniksi
tabVarDesc <- c("Q1a Working mother can have warm relation with child ",
                "Q1b Pre-school child suffers through working mother",
                "Q1c Family life suffers through working mother",
                "Q1d Women’s preference: home and children",
                "Q1e Being housewife is satisfying",
                "Q2a Both should contribute to household income",
                "Q2b Men’s job is earn money, women’s job household",
                "Q3a Should women work: Child under school age",
                "Q3b Should women work: Youngest kid at school",
                "Respondents age ",
                "Respondents gender",
                "Highest completed degree of education: Categories for international comparison",
                "Main status: work, unemployed, in education...",
                "Top-Bottom self-placement (10 pt scale)",
                "How many children in household: children between [school age] and 17 years of age",
                "Legal partnership status: married, civil partership...",
                "Place of living: urban - rural"
              )
#tabVarDesc

# Taulukko

# luodaan df - varoitus: data_frame() is deprecated, use tibble” (4.2.20),
# vaihdetaan tibbleen (21.2.20)

# jhVarTable1.df <- data_frame(tabVarnames,tabVarDesc) OLD
jhVarTable1.tbl <- tibble(tabVarnames,tabVarDesc)
cols_jhVarTable1 <- c("muuttuja","kysymyksen tunnus, lyhennetty kysymys")
colnames(jhVarTable1.tbl) <- cols_jhVarTable1
#str(jhVarTable1.tbl)
# Lyhyet kysymykset englanniksi

knitr::kable(jhVarTable1.tbl, booktab = TRUE,
               caption = "ISSP2012:Työelämä ja perhearvot - kysymykset")



knitr::include_graphics('img/substvar_fi_Q1Q2.png')

# UUSI DATA 30.1.20
#
# LUETAAN DATA G1_1_data2.Rmd - tiedostossa, luodaan faktorimuuttujat
# G1_1_data_fct1.Rmd-tiedostossa -> ISSP2012jh1d.dat (df)
# 23 muuttujaa (9 substanssimuuttujaa, 8 taustamuuttujaa, 3 maa-muuttujaa, 3 metadatamuuttujaa)
# 25 maata.
# Poistettu 146 havaintoa, joilla SEX tai AGE puuttuu
# Johdattelevassa esimerkissä kuusi maata, kaksi taustamuuttujaa ja yksi kysymys
# (V6/Q1b)


# Kuusi maata

countries_esim1 <- c(56, 100, 208, 246, 276, 348) #BE,BG,DK,FI,DE,HU
ISSP2012esim3.dat <- filter(ISSP2012jh1d.dat, V4 %in% countries_esim1)
# str(ISSP2012esim3.dat) - pitkä listaus pois (24.2.20)

#neljä maamuuttujaa, kysymys Q1b, ikä ja sukupuoli

vars_esim1 <- c("C_ALPHAN", "V3", "maa","maa3", "Q1b", "sp", "ika")
ISSP2012esim2.dat <- select(ISSP2012esim3.dat, all_of(vars_esim1))

str(ISSP2012esim2.dat) # 8542 obs. of  7 variables, ja sama 8.6.2020
# C_ALPHAN: chr, maa: Factor w/ 25

# Poistetaan havainnot, joilla Q1b - muuttujassa puuttuva tieto 'NA'
# sum(is.na(ISSP2012esim2.dat$Q1b)) = 399

ISSP2012esim1.dat <- filter(ISSP2012esim2.dat, !is.na(Q1b))

#str(ISSP2012esim1.dat) # 8143 obs. of  6 variable

# Tarkistuksia (3.2.20)
#
#fct_count(ISSP2012esim1.dat$sp)
#fct_count(ISSP2012esim1.dat$Q1b)
#fct_count(ISSP2012esim1.dat$maa)
#fct_count(ISSP2012esim1.dat$maa3)
#
#summary(ISSP2012esim1.dat$sp)
#sp: 3799 + 4344 = 8143
#summary(ISSP2012esim1.dat$Q1b)
#  S      s      ?     e      E
# 810 + 1935 + 1367 + 2125 + 1906 = 8143
#
# EDELLINEN DATA - havaintojen määrät samat kuin uudella datalla (31.1.20)
#
# 8557 obs. ennen kuin sexagemissing poistettiin, nyt 8542, 8557-8542 = 15
#
# Poistetaan havainnot joissa puuttuva tieto muuttujassa V6 (Q1b) n = 399
# 8542-399 = 8143

# Tyhjät "faktorilabelit" on poistettava

 ISSP2012esim1.dat <- ISSP2012esim1.dat %>%
     mutate(maa = fct_drop(maa),
            maa3 = fct_drop(maa3)
            )

#summary(ISSP2012esim1.dat$maa)
#summary(ISSP2012esim1.dat$maa3)
#
# str(ISSP2012esim1.dat$maa)
# attributes(ISSP2012esim1.dat$maa)
#
# str(ISSP2012esim1.dat$maa3)
# attributes(ISSP2012esim1.dat$maa3)
#
#ISSP2012esim1.dat %>% tableX(maa, Q1b, type = "count")
#fct_count(ISSP2012esim1.dat$Q1b)
# fct_count(ISSP2012esim1.dat$sp)
# fct_unique(ISSP2012esim1.dat$maa)
# fct_count(ISSP2012esim1.dat$maa)
#ISSP2012esim1.dat %>% tableX(maa, C_ALPHAN, type = "count")
#
# maa3 - siistitään "faktorilabelit" kaksikirjaimisiksi
#
# ISO 3166 Code V3 - maiden jaot
#  5601     BE-FLA-Belgium/ Flanders
#  5602     BE-WAL-Belgium/ Wallonia
#  5603     BE-BRU-Belgium/ Brussels
# 27601     DE-W-Germany-West
# 27602     DE-E-Germany-East
# Tähän pitäisi päästä
# levels = c("100","208","246","348","5601","5602","5603","27601","27602"),
# labels = c("BG","DK","FI","HU","bF","bW","bB","dW","dE"))
# levels(ISSP2012esim1.dat$maa3)

ISSP2012esim1.dat <- ISSP2012esim1.dat %>%
        mutate(maa3 =
                fct_recode(maa3,
                 "BG" = "BG-Bulgaria",
                 "DK" = "DK-Denmark",
                 "FI" = "FI-Finland",
                 "HU" = "HU-Hungary",
                 "bF" = "BE-FLA-Belgium/ Flanders",
                 "bW" = "BE-WAL-Belgium/ Wallonia",
                 "bB" = "BE-BRU-Belgium/ Brussels",
                 "dW" = "DE-W-Germany-West",
                 "dE" = "DE-E-Germany-East")
               )
# tarkistuksia
#levels(ISSP2012esim1.dat$maa3)
# str(ISSP2012esim1.dat$maa3) # 9 levels
#summary(ISSP2012esim1.dat$maa3)
#
# TÄSSÄ TOISTOA! (4.2.20)
# Muutetaan muuttujien "maa" ja "maa3" arvojen (levels) järjestys samaksi kuin
# alkuperäisen muuttujan C_ALPHAN. Helpomi verrata aikaisempiin tuloksiin.

# "alkuperäinen" maa talteen
ISSP2012esim1.dat$maa2 <- ISSP2012esim1.dat$maa

ISSP2012esim1.dat <- ISSP2012esim1.dat %>%
        mutate(maa =
                fct_relevel(maa,
                            "BE",
                            "BG",
                            "DE",
                            "DK",
                            "FI",
                            "HU"))
ISSP2012esim1.dat <- ISSP2012esim1.dat %>%
        mutate(maa3 =
                fct_relevel(maa3,
                        "bF",
                        "bW",
                        "bB",
                        "BG",
                        "dW",
                        "dE",
                        "DK",
                        "FI",
                        "HU"))

# Tarkistus
#ISSP2012esim1.dat %>% tableX(maa2,maa, type = "count")
# "alkuperäinen" maa talteenISSP2012esim1.dat %>% tableX(maa,C_ALPHAN, type = "count")
# "alkuperäinen" maa talteenstr(ISSP2012esim1.dat)

# Taulukoita (31.1.2020) ja tarkistuksia
#
# toinen maa-muuttuja, jossa Saksan ja Belgian jako
#  V3
#  5601     BE-FLA-Belgium/ Flanders
#  5602     BE-WAL-Belgium/ Wallonia
#  5603     BE-BRU-Belgium/ Brussels
# 27601     DE-W-Germany-West
# 27602     DE-E-Germany-East

# Tarkastuksia

# assert_that ehkä tarpeeton - expect_equivalet testaa levelien
# järjestyksen ja määrän (20.2.20)

validate_that(length(levels(ISSP2012esim1.dat$sp)) == 2)
validate_that(are_equal(levels(ISSP2012esim1.dat$sp),
                c("m", "f")))

validate_that(length(levels(ISSP2012esim1.dat$maa)) == 6)

validate_that(are_equal(levels(ISSP2012esim1.dat$maa),
                  c("BE", "BG", "DE", "DK", "FI", "HU")))

validate_that(length(levels(ISSP2012esim1.dat$maa3)) == 9)

validate_that(are_equal(levels(ISSP2012esim1.dat$maa3),
                 c("bF","bW","bB", "BG","dW","dE","DK", "FI", "HU")))

validate_that(length(levels(ISSP2012esim1.dat$Q1b)) == 5)
validate_that(are_equal(levels(ISSP2012esim1.dat$Q1b),
               c("S", "s", "?", "e", "E")))

# testthat - paketti - pois käytöstä 16.9.20
# expect_ ei anna ok-ilmoitusta, ainoastaan virheilmoituksen? (11.4.20)
# expect_equivalent(levels(ISSP2012esim1.dat$maa),
#                  c("BE", "BG", "DE", "DK", "FI", "HU"))
# expect_equivalent(levels(ISSP2012esim1.dat$maa3),
#                  c("bF","bW","bB", "BG","dW","dE","DK", "FI", "HU"))
# expect_equivalent(levels(ISSP2012esim1.dat$sp), c("m", "f"))
# expect_equivalent(levels(ISSP2012esim1.dat$Q1b),
#                  c("S", "s", "?", "e", "E"))
#
# ISSP2012esim1.dat %>% tableX(maa,ika,type = "row_perc")
#
# Riviprofiilit
#
# ISSP2012esim1.dat %>% tableX(maa,ika,type = "row_perc")
# ISSP2012esim1.dat %>% tableX(maa,sp ,type = "row_perc")
#
#
# Kysymyksen Q1b vastaukset
#
#ISSP2012esim1.dat %>% tableX(maa,Q1b,type = "row_perc")
#
#ISSP2012esim1.dat %>% tableX(maa3,Q1b,type = "row_perc")
#
# str(ISSP2012esim1.dat) # 8143 obs. of  7 variable,
# sama kuin vanhassa Galku-koodissa.
#
# str(ISSP2012esim1.dat) # 8143 obs. of  7 variable,
# sama kuin vanhassa Galku-koodissa.


taulu2 <- ISSP2012esim1.dat %>% tableX(maa, Q1b, type = "cell_perc")
knitr::kable(taulu2,digits = 2, booktabs = TRUE,
             caption = "Kysymyksen Q1b vastaukset, suhteelliset frekvenssit")


taulu3 <- ISSP2012esim1.dat %>% tableX(maa,Q1b,type = "row_perc")

knitr::kable(taulu3,digits = 2, booktabs = TRUE,
             caption = "Kysymyksen Q1b vastaukset, riviprosentit")


taulu4 <- ISSP2012esim1.dat %>% tableX(maa,Q1b,type = "col_perc")

knitr::kable(taulu4,digits = 2, booktabs = TRUE,
             caption = "Kysymyksen Q1b vastaukset, sarakeprosentit")

# CA tässä, jotta saadaan rivi- ja sarakeprofiilikuvat
# Lasketaan samalla CA-ratkaisu riviprofiilitaulkolle (maille samat painot)

simpleCA1 <- ca(~maa + Q1b,ISSP2012esim1.dat)

# Maiden järjestys kääntää kuvan (1.2.20) - esimerkki on
# vähän kuriositeetti. Kartta voi tietysti "flipata" koordintaattien suhteen ainakin
# neljällä tavalla (? 180 astetta molempien akseleiden ympäri molempiin suuntiin?)
# (18.2.20). Tämän maa2-muuttujaa käyttävän kuvan voi jättää pois (8.4.20)

# simpleCA2 <- ca(~maa2 + Q1b,ISSP2012esim1.dat)

# Oikeastaan maiden vertailussa pitäisi niiden massat skaalata yhtä suuriksi, tässä
# pikainen kokeilu (20.2.20)
# Riviprosentit taulukoksi, nimet sarakkeille ja riveille (ei kovin robustia...)


johdesim1_rowproc.tab <- simpleCA1$N / rowSums(simpleCA1$N)
colnames(johdesim1_rowproc.tab) <- c("S" ,"s" ,"?","e", "E")
rownames(johdesim1_rowproc.tab) <- c("BE", "BG", "DE", "DK", "FI", "HU")

# Miten tibblenä? Ei toimi, ei maa-muuttujaa ollenkaan
# johdesim1_rowproc.tbl <- as_tibble(johdesim1_rowproc.tab)
# str(johdesim1_rowproc.tbl)

# TARKISTUKSIA (20.2.20)
# johdesim1_rowproc.tab
# rowSums(johdesim1_rowproc.tab)
# str(johdesim1_rowproc.tab)


simpleCA3 <- ca(johdesim1_rowproc.tab)


# Kartta piirretään koodilohkossa simpleCAmap1, r. 773 noin.

# Riviprosentit tarkistusta varten
#        S  s   ?   e   E
#BE 9.49    22.40   21.76   27.42   18.93
#BG 12.81   42.89   22.26   20.63   1.41
#DE 9.63    21.88   11.55   31.39   25.55
#DK 5.04    17.15   10.95   16.71   50.14
#FI 4.23    16.94   13.42   38.11   27.30
#HU 21.97   28.89   22.57   19.06   7.52
#
# Ja datan saa leikepöydän kautta, jos on tarve pikatarkistuksiin
# read <- read.table("clipboard")

#mutkikas kuvan piirto - sarakeprofiilit vertailussa
#ggplot vaatii df-rakenteen ja 'long data' - muotoon
##https://stackoverflow.com/questions/9563368/create-stacked-barplot
# -where-each-stack-is-scaled-to-sum-to
# Pitkä https-linkki kahdella rivillä
#
# käytetään ca - tuloksia
apu1 <- (simpleCA1$N)
colnames(apu1) <- c("S", "s", "?", "e", "E")
rownames(apu1) <- c("BE", "BG", "DE", "DK", "FI", "HU")
apu1_df <- as.data.frame(apu1)
#lasketan rivien reunajakauma
apu1_df$ka_sarake <- rowSums(apu1_df)
#muokataan 'long data' - muotoon
apu1b_df <- melt(cbind(apu1_df, ind = rownames(apu1_df)), id.vars = c('ind'))

p <- ggplot(apu1b_df, aes(x = variable, y = value, fill = ind)) +
         geom_bar(position = "fill", stat = "identity") +
         scale_y_continuous(name = " ",labels = percent_format())
p <- p + labs(fill = "maa")
p + scale_x_discrete(name = "Q1b - vastauskategoriat")
# apu1_df
# apu1b_df


# riviprofiilit ja keskiarvorivi -  18.9.2018
apu2_df <- as.data.frame(apu1)
apu2_df <- rbind(apu2_df, ka_rivi = colSums(apu2_df))

#apu2_df
#str(apu2_df)
## typeof(apu2_df) # what is it?
## class(apu2_df) # what is it? (sorry)
## storage.mode(apu2_df) # what is it? (very sorry)
## length(apu2_df) # how long is it? What about two dimensional
## objects?
# attributes(apu2_df)

# temp1 <- cbind(apu2_df, ind = rownames(apu2_df))
# temp1
##muokataan 'long data' - muotoon
apu2b_df <- melt(cbind(apu2_df, ind = rownames(apu2_df)), id.vars = c('ind'))
# str(apu2b_df)
# glimpse(apu2b_df)

#
#ggplot(apu2b_df, aes(x = value, y = ind, fill = variable)) +
#       geom_bar(position = "fill", stat ="identity") +
#       #coord_flip() +
#        scale_x_continuous(labels = percent_format())

#versio2 toimii (18.9.2018)

p <- ggplot(apu2b_df, aes(x = ind, y = value, fill = variable)) +
       geom_bar(position = "fill", stat = "identity") +
       coord_flip() +
        scale_y_continuous(name = " ",labels = percent_format())
p <- p + labs(fill = "Q1b")
p + scale_x_discrete(name = " ")



# simpleCA1 luotu aikaisemmin profiilikuvia varten koodilohkossa EkaCA
# HUOM! xlab ja ylab, prosenttiosuudet ensin katsottu ja sitten kirjoitettu
# tässä. Vertaa scree-plot - tietoon!


#par(cex = 1)
plot(simpleCA1, map = "symmetric", mass = c(TRUE,TRUE),
     xlab = "Dimensio 1: moderni/liberaali - perinteinen/konservatiivinen (76%)",
     ylab = "Dimensio 2: maltillinen/epävarma - radikaali/jyrkkä/varma (15.1%)",
     main = "symmetrinen kartta 1",
     sub = "Maiden massat eri suuruisia (otoskoko), pisteiden koko suhteessa massaan")

# jatkossa plot - main on kuvan tyyppi (symmetrinen, kontribuutio jne),
# koodilohkon fig.cap "ylimmän tason" otsikko.

# Akseleiden tekstit (Dimensio 1....jne) asetettu käsin, ikävä kyllä myös
# selitetyn inertian osuus. CA-kartoissa tämä on niin oleellinen asia,
# että akselien nimet voi muutttaa vasta esitysgrafiikassa, ei data-analyysissä.
# Dim1 ja Dim2  kuuluvat kuviin.

# par(cex = 1) - asetus ennen plot-komenota muuttaa valitettavasti "kaiken" kokoa.
# Antaa olla, kun on graafista data-analyysiä. Selkeys tärkeämpää kuin ulkoasu.



# asymmetrinen kartta - rivit pc ja sarakkeet sc
# sarakkeet vektorikuvina

# par(cex = 0.7)
plot(simpleCA1, map = "rowprincipal",
     arrows = c(FALSE,TRUE),
     main = "asymmetrinen kartta 1"
    )


knitr::include_graphics('img/simpleCAasymmTulk2.png')


#par(cex = 0.6)
plot(simpleCA1, map = "rowgreen",
     contrib = c("absolute", "absolute"),
     mass = c(TRUE,TRUE),
     arrows = c(FALSE, TRUE),
     main = "kontribuutiokartta 1 - pisteen koko suhteessa massaan",
     sub = "sarakevektorin ja rivipisteiden värin tummuus = absoluuttinen kontribuutio")


#par(cex = 0.7)
plot(simpleCA1, map = "rowgreen",
     contrib = c("relative", "relative"),
     mass = c(TRUE,TRUE),
     arrows = c(FALSE, TRUE),
     main = "kontribuutiokartta 2 - pisteen koko suhteessa massaan",
     sub = "sarakevektorin ja pisteen värin tummuus = suhteellinen kontribuutio")


# Sama kartta - maiden massat vakiotu - simpleCA3 luotu koodilohkossa EkaCA
# CA:n lähtötietona riviprofiilit

#par(cex = 0.8)
plot(simpleCA3, map = "symmetric", mass = c(TRUE,TRUE),
main = "symmetrinen kartta 2 ",
sub = "Maidet massat vakioitu (riviprofiilidata)")


plot(simpleCA3, map = "rowgreen",
     contrib = c("absolute", "absolute"),
     mass = c(TRUE,TRUE),
     arrows = c(FALSE, TRUE),
     main = "kontribuutiokartta 3",
     sub = "sarakevektorin ja rivipisteiden värin tummuus = absoluuttinen kontribuutio, riviprofiilidata")

# riviprofiilitaulukko aiheuttaa virheen PDF-tulostuksessa, JH_capaper.Rmd
# tiedoston voi kuitenkin renderöidä knit-napilla RStudiossa pdf-tiedostoksi.


BeDealueTable <- ISSP2012esim1.dat %>% tableX(maa3, Q1b, type = "row_perc")

knitr::kable(BeDealueTable , digits = 2, booktabs = TRUE,
           caption = "Q1b vastaukset, Saksan ja Belgian alueet")


# Belgian ja Saksan aluejako maa3-muuttujassa
# str(ISSP2012esim1.dat$maa3)
# attributes(ISSP2012esim1.dat$maa3)

suppoint1_df1 <- select(ISSP2012esim1.dat, maa3,Q1b)

# Taulukoksi jotta saadaan lisättyä Saksan ja Belgian maa-profiilit täydentäviksi
# pisteiksi.

suppoint1_tab1 <- table(suppoint1_df1$maa3, suppoint1_df1$Q1b)

# tarkistus 1
# suppoint1_tab1

# Maaprofiilit lisäpisteiksi
suppoint2_df <- filter(ISSP2012esim1.dat, (maa == "BE" | maa == "DE"))
suppoint2_df <- select(suppoint2_df, maa, Q1b)
# Poistetaan maa-faktroin tyhjät luokat (14.11.2020)
suppoint2_df <- suppoint2_df %>%
    mutate(maa = fct_drop(maa)
    )


#glimpse(suppoint2_df)
suppoint2_tab1 <- table(suppoint2_df$maa, suppoint2_df$Q1b)

# tarkistus 1
# suppoint2_tab1

# lisätään rivit maa3-muuttujan taulukkoon

suppoint1_tab1 <- rbind(suppoint1_tab1, suppoint2_tab1)

# suppoint1_tab1 

# suppoint1_tab2 <- read_rds("suppoint1tab1.rds") - testaus joka siirsi virheen 07-rmd-tiedostoon. Sama virheilmoitustyyppi.

suppointCA2 <- ca(suppoint1_tab1[,1:5], suprow = 10:11)

# Sama kartta ilman täydentäviä pisteitä

suppointCA2b <- ca(suppoint1_tab1[1:9,1:5])

# par(cex = 0.6)
plot(suppointCA2, main = "Symmetrinen kartta 1 ",
     # mass = c(TRUE, TRUE),
     # contrib = c(TRUE, FALSE),
     sub = "Täydentävät pisteet DE ja BE" )



plot(suppointCA2b, main = "kontribuutiokartta 1 - absoluuttiset kontribuutiot",
        map = "rowgreen",
        arrows = c(FALSE, TRUE),
        mass = c(TRUE, TRUE),
        contrib = c("absolute","absolute"),
        sub = "Massat: pisteiden ja symbolien koko " )


print(suppointCA2)


summary(suppointCA2)

suppointCA3 <- ca(~maa3 + Q1b,ISSP2012esim1.dat, nd = 3)

# summary(suppointCA3)
# Error in rsc %*% diag(sv) : non-conformable arguments
# outo juttu, ei toimi! - TÄMÄ POISTETAAN

plot(suppointCA3, dim = c(1,2),
                main = "Kolmen dimension ratkaisu",
                sub = "symmetrinen kartta - 1. ja 2. dimensio")

plot(suppointCA3, dim = c(1,3),
                main = "Kolmen dimension ratkaisu 1",
                sub = "symmetrinen kartta - 1. ja 3. dimensio")

plot(suppointCA3, dim = c(2,3),
                main = "Kolmen dimension ratkaisu 2",
                sub = "symmetrinen kartta - 2. ja 3. dimensio")


knitr::include_graphics('img/3dSymMap_1.PNG')


knitr::include_graphics('img/3dSymMap_2.PNG')

# Iän ja sukupuolen vuorovaikutusmuuttujia
#
# Uusi R-data: ISSP2012esim1b.dat2esim1b)
#
# Ikäluokat age_cat
# AGE 1=15-25, 2 =26-35, 3=36-45, 4=46-55, 5=56-65, 6= 66 and older
#
# summary(ISSP2012esim1.dat$AGE)
# hist(ISSP2012esim1.dat$ika)

ISSP2012esim1b.dat <- mutate(ISSP2012esim1.dat,
                      age_cat = ifelse(ika %in% 15:25, "1",
                        ifelse(ika %in% 26:35, "2",
                        ifelse(ika %in% 36:45, "3",
                        ifelse(ika %in% 46:55, "4",
                        ifelse(ika %in% 56:65, "5", "6"))))))


ISSP2012esim1b.dat <- ISSP2012esim1b.dat %>%  
        mutate(age_cat = as_factor(age_cat)) # järjestys omituinen!(4.2.20)

# Tarkistuksia
# str(ISSP2012esim2.dat$age_cat)
# levels(ISSP2012esim2.dat$age_cat)
# ISSP2012esim2.dat$age_cat %>% summary()

# Järjestetään ikäluokat uudelleen

ISSP2012esim1b.dat <- ISSP2012esim1b.dat %>%
        mutate(age_cat =
                fct_relevel(age_cat,
                            "1",
                            "2",
                            "3",
                            "4",
                            "5",
                            "6")
               )

# Tarkistuksia

# Iso taulukko, voi tarkistaa että muunnos ok.
# test6 %>% tableX(AGE, age_cat, type = "count")
# taulu42 <- ISSP2012esim2.dat %>% tableX(maa,age_cat,type = "count")
# kable(taulu42,digits = 2, caption = "Ikäluokka age_cat")
#

# Taulukoita (4.2.20)

#ISSP2012esim1b.dat %>%
#    tableX(maa,age_cat,type = "count") %>%
#    kable(digits = 2, caption = "Ikäluokka age_cat")
#
#ISSP2012esim1b.dat %>%
#    tableX(maa,age_cat,type = "row_perc") %>%
#    kable(digits = 2, caption = "age_cat: suhteelliset frekvenssit")

# ga - ikäluokka ja sukupuoli

ISSP2012esim1b.dat <- mutate(ISSP2012esim1b.dat,
                        ga = case_when((age_cat == "1")&(sp == "m") ~ "m1",
                                       (age_cat == "2")&(sp == "m") ~ "m2",
                                       (age_cat == "3")&(sp == "m") ~ "m3",
                                       (age_cat == "4")&(sp == "m") ~ "m4",
                                       (age_cat == "5")&(sp == "m") ~ "m5",
                                       (age_cat == "6")&(sp == "m") ~ "m6",
                                       (age_cat == "1")&(sp == "f") ~ "f1",
                                       (age_cat == "2")&(sp == "f") ~ "f2",
                                       (age_cat == "3")&(sp == "f") ~ "f3",
                                       (age_cat == "4")&(sp == "f") ~ "f4",
                                       (age_cat == "4")&(sp == "f") ~ "f4",
                                       (age_cat == "5")&(sp == "f") ~ "f5",
                                       (age_cat == "6")&(sp == "f") ~ "f6",
                                       TRUE ~ "missing"
                                  ))

#ISSP2012esim1.dat %>% tableX(ga,ga2) # tarkistus
# muuttujien tarkistuksia 19.9.2018
# str(ISSP2012esim1b.dat$ga) # chr-muuttuja, mutta toimii (4.2.20)

#Tulostetaan taulukkoina ga - muuttuja

#ISSP2012esim1b.dat %>% tableX(maa,ga,type = "count") %>%
#kable(digits = 2, caption = "Ikäluokka ja sukupuoli ga")

#ISSP2012esim1b.dat %>% tableX(maa,ga,type = "row_perc") %>%
#kable(digits = 2, caption = "ga: suhteelliset frekvenssit")


gaTestCA1 <- ca(~ga + Q1b,ISSP2012esim1b.dat)


# Maapisteiden pääkoordinaatit janojen piirtämiseen

gaTestCA1.rpc <- gaTestCA1$rowcoord %*% diag(gaTestCA1$sv)

# par(cex = 0.6)
plot(gaTestCA1, main = "symmetrinen kartta, m = mies, f = nainen",
     sub = "1=15-25, 2 =26-35, 3=36-45, 4=46-55, 5=56-65, 6= 66 tai vanhempi ")
# naiset
lines(gaTestCA1.rpc[1:6,1],gaTestCA1.rpc[1:6,2])
#miehet
lines(gaTestCA1.rpc[7:12,1],gaTestCA1.rpc[7:12,2], col = "red")



summary(gaTestCA1)

ISSP2012esim1b.dat <- mutate(ISSP2012esim1b.dat,
                             maaga = paste(maa, ga, sep = ""))

# tarkistus, muunnos ok
# ISSP2012esim1b.dat %>% tableX(maa, maaga)
# head(ISSP2012esim2.dat)
# str(ISSP2012esim2.dat)


maagaCA1 <- ca(~maaga + Q1b,ISSP2012esim1b.dat)


par(cex = 0.5)
plot(maagaCA1, main = "symmetrinen kartta 1" )


# print(maagaCA1)

summary(maagaCA1)


# Osajoukon CA: Tanska, Saksa ja Suomi
maagaCA2sub2 <- ca(~maaga + Q1b,ISSP2012esim1b.dat,subsetrow = 25:60)


par(cex = 0.8)
plot(maagaCA2sub2, main = "Q1b: Lapsi kärsii jos äiti käy töissä",
     sub = "symmetrinen kartta - osajoukko Tanska, Saksa ja Suomi)"
   )


par(cex = 0.6)
plot(maagaCA2sub2, map = "rowgreen",
     mass = c(TRUE, TRUE),
     contrib =c("relative", "absolute"),
     arrows = c(FALSE, TRUE),
     main = "Kontribuutiokartta: sarakkeiden(abs.) ja rivien(rel.) värisävy",
     sub = "massat = pisteiden koko"
      )

# ca-tulosobjekti maagaCA2sub2, DK DE FI

maagaLinesDKDEFI <- cacoord(maagaCA2sub2, type = "symmetric")
maagaLinesDKDEFI <- maagaLinesDKDEFI$rows[ , 1:2]
# maagaLinesDKDEFI # tarkistus
par(cex = 0.6)
plot(maagaCA2sub2,
     sub = "symmetrinen kartta - Tanska, Saksa ja Suomi (subset ca)")
lines(maagaLinesDKDEFI[1:6,1],maagaLinesDKDEFI[1:6,2], col="blue") #DEf
lines(maagaLinesDKDEFI[7:12,1],maagaLinesDKDEFI[7:12,2], col="red")  #DEm
lines(maagaLinesDKDEFI[13:18,1],maagaLinesDKDEFI[13:18,2], col="blue") #DKf
lines(maagaLinesDKDEFI[19:24,1],maagaLinesDKDEFI[19:24,2], col="red")  #DKm
lines(maagaLinesDKDEFI[25:30,1],maagaLinesDKDEFI[25:30,2], col="blue") #FIf
lines(maagaLinesDKDEFI[31:36,1],maagaLinesDKDEFI[31:36,2], col="red")  #FIm


# Tarkastetaan numeeriset tulokset
summary(maagaCA2sub2)

# Jos suhteeelinen inertia kaikilla rivelillä sama
# 1000/36 = 28


# Belgia, Bulgaria ja Unkari analysoidaan tiiviisti
# Belgia on vähän välitapaus Bulgarian ja Unkarin ja kolmen ensimmäisen maan
# kanssa. Kokeiluja voi tehdä neljällä maaryhmällä, kuvan lukukelpoisuus
# ratkaisee.

#BGHUsubset <- c(13:24,61:72)
#BEDEDKFIsubset <- c(1:12, 25:36, 37:48, 49:60)
#DEDKFIsubset <- c(25:36, 37:48, 49:60)

BEBGHUsubset <- c(1:12,13:24,61:72)
maagaCA2sub3 <- ca(~maaga + Q1b,ISSP2012esim1b.dat,subsetrow = BEBGHUsubset)


par(cex = 0.6)
plot(maagaCA2sub3, 
     mass = c(TRUE, TRUE),
     contrib =c("relative", "absolute"),
     arrows = c(FALSE, FALSE),
     main = "symmetrinen kartta: sarakkeiden ja rivien suhteelliset kontribuutiot värisävynä ",
     sub = "massat = pisteiden koko"
      )


par(cex = 0.6)
plot(maagaCA2sub3, map = "rowgreen",
     mass = c(TRUE, TRUE),
     contrib =c("relative", "absolute"),
     arrows = c(FALSE, TRUE),
     main = "Kontribuutiokartta: sarakkeiden(abs.) ja rivien(abs.) värisävy",
     sub = "massat = pisteiden koko"
      )


# Vilkaistaa numeerisia tuloksia, kopioidaan tekstiin jos on tarpeen
# maagaCA2sub3
 summary(maagaCA2sub3)

# kahden osaratkaisun kokonaisinertia

# 0.143551 + 0.119602 = 0.263153
# koko datalla 0.263154


knitr::include_graphics('img/stacked1.png')


# Data
ISSP2012Concat1jh.dat <- select(ISSP2012esim1b.dat, Q1b, maa,sp, age_cat)

# mjca-funktiota ->  Burt-matriisi
Concat1jh.Burt <- mjca(ISSP2012Concat1jh.dat, ps="")$Burt

# Burt-matriisi symmetrinen
#dim(Concat1jh.Burt)
# 19 x 19
#rownames(Concat1jh.Burt)
#[1] "Q1bS"     "Q1bs"     "Q1b?"     "Q1be"     "Q1bE"     "maaBE"    "maaBG"    "maaDE"    "maaDK"
#[10] "maaFI"    "maaHU"    "spm"      "spf"      "age_cat1" "age_cat2" "age_cat3" "age_cat4" "age_cat5"
#[19] "age_cat6"

# maat - vastaukset
ISSP2012Concat2jh.dat <- Concat1jh.Burt[6:11, 1:5]
# ISSP2012Concat2jh.dat
# sukupuoli ja vastaukset
ISSP2012Concat2jh.dat <- rbind(ISSP2012Concat2jh.dat, Concat1jh.Burt[12:13 ,1:5])
# ISSP2012Concat2jh.dat
# ikäluokka ja vastaukset
ISSP2012Concat2jh.dat <- rbind(ISSP2012Concat2jh.dat, Concat1jh.Burt[14:19 ,1:5])
# ISSP2012Concat2jh.dat

Concat1jh.CA1 <- ca(ISSP2012Concat2jh.dat)


# Käännetään kuva x-akselin ympäri
Concat1jh.CA1$rowcoord[, 2] <- -Concat1jh.CA1$rowcoord[, 2]
Concat1jh.CA1$colcoord[, 2] <- -Concat1jh.CA1$colcoord[, 2]

# Siistitään muuttujien nimet
Concat1jh.CA1$colnames <- c("S", "s", "?", "e", "E")
Concat1jh.CA1$rownames <- c("BE", "BG", "DE", "DK", "FI", "HU", "m", "f",
                            "a1", "a2", "a3", "a4", "a5", "a6")


# pisteiden kasautumien haittaa haittaa tulkintaa

par(cex = 0.6) 
plot(Concat1jh.CA1,
     main = "Pinottu taulukko - symmetrinen kartta",
     sub = "ikäluokat a1-a6, m = miehet, f = naiset"
     )


summary(Concat1jh.CA1)

# 14 riviä, inertiakontribuution keskiarvo
# 1000/14 = 71 


par(cex = 0.6)
plot(Concat1jh.CA1, map = "rowgreen",
     #mass = c(TRUE, TRUE) ei oikein erotu kuvassa
     contrib =c("relative", "absolute"),
     arrows = c(FALSE, TRUE),
     main = "Pinottu taulukko, kontribuutiokartta (sarakkeet absoluutinen, rivit suhteellinen)",
     sub =  "taustamuuttujat a1-a6 ikäluokat, m = miehet, f = naiset"
     )

# Tätä dataa ei käytetä - pelkät kysymykset
# str(ISSP2012jh1d.dat) - luotu skripteissä G1_1_data2.Rmd ja G1_1_data_fct1.Rmd
# Tarkistukset näkyvät Galkussa - tässä ei tulosteta
# Kommentoidaan pois tarkistuksia (14.11.2020)
#Valitaan muuttujat joissa puuttuva tieto on koodattu muuttujan arvoksi

MCAvars1 <-  c("Q1am","Q1bm", "Q1cm", "Q1dm","Q1em","Q2am","Q2bm","edum",
                 "sostam", "urbrum", "maa", "ika", "sp" )

MCAdata1jh.dat <- ISSP2012jh1d.dat %>% select(all_of(MCAvars1))

#dim(MCAdata1jh.dat)
# names(MCAdata1jh.dat)

# luodaan ikaluokka-muuttuja ja ikäluokka-sukupuoli - muuttuja
#age_cat
#ikä 1=15-25, 2 =26-35, 3=36-45, 4=46-55, 5=56-65, 6= 66 and older

MCAdata1jh.dat <- mutate(MCAdata1jh.dat, age_cat = ifelse(ika %in% 15:25, "1",
                                ifelse(ika %in% 26:35, "2",
                                ifelse(ika %in% 36:45, "3",
                                ifelse(ika %in% 46:55, "4",
                                ifelse(ika %in% 56:65, "5", "6"))))))

# str(MCAdata1jh.dat$age_cat)

MCAdata1jh.dat <- MCAdata1jh.dat %>%
        mutate(age_cat = as_factor(age_cat))
#tarkastuksia - outo järjestys
#levels(MCAdata1jh.dat$age_cat)
# str(MCAdata1jh.dat$age_cat)

MCAdata1jh.dat<- MCAdata1jh.dat %>%
        mutate(age_cat = fct_relevel(age_cat,
                                   "1",
                                   "2",
                                   "3",
                                   "4",
                                   "5",
                                   "6"))

# Tarkistuksia(16.10.20)

#MCAdata1jh.dat %>%
#        tableX(maa,age_cat,type = "count") #%>%
#        #kable(digits = 2, caption = "Ikäluokka age_cat")

#MCAdata1jh.dat %>%
#        tableX(maa,age_cat,type = "row_perc") #%>%
#        #kable(digits = 2, caption = "age_cat: suhteelliset frekvenssit")


# Ikäluokka-sukupuoli - muuttuja
MCAdata1jh.dat <- mutate(MCAdata1jh.dat,
                             ga = case_when((age_cat == "1")&(sp == "m") ~ "m1",
                                (age_cat == "2")&(sp == "m") ~ "m2",
                                (age_cat == "3")&(sp == "m") ~ "m3",
                                (age_cat == "4")&(sp == "m") ~ "m4",
                                (age_cat == "5")&(sp == "m") ~ "m5",
                                (age_cat == "6")&(sp == "m") ~ "m6",
                                (age_cat == "1")&(sp == "f") ~ "f1",
                                (age_cat == "2")&(sp == "f") ~ "f2",
                                (age_cat == "3")&(sp == "f") ~ "f3",
                                (age_cat == "4")&(sp == "f") ~ "f4",
                                (age_cat == "4")&(sp == "f") ~ "f4",
                                (age_cat == "5")&(sp == "f") ~ "f5",
                                (age_cat == "6")&(sp == "f") ~ "f6",
                                TRUE ~ "missing"
                                ))


#Sosiaalinen status: oma arvio "Top-Bottom self-placement"
#str(ISSP2012jh1d.dat$sosta)
#str(ISSP2012jh1d.dat$urbru)
#str(ISSP2012jh1d.dat$edu)
#Koulutustaso
#str(ISSP2012jh1d.dat$edu)

#Asuipaikka
#str(ISSP2012jh1d.dat$urbru)

# Muunnetaan faktorimuuttujia, mahdollisimman lyhyet tunnisteet kategorioille
MCAdata1jh.dat <- MCAdata1jh.dat %>%
mutate(E = fct_recode(edum,
        "1" = "No formal education",
        "2" = "Primary school (elementary school)",
        "3" = "Lower secondary (secondary completed does not allow entry to university: obligatory school)",
        "4" = "Upper secondary (programs that allows entry to university",
        "5" = "Post secondary, non-tertiary (other upper secondary programs toward labour market or technical formation)",
        "6" = "Lower level tertiary, first stage (also technical schools at a tertiary level)",
        "7" = "Upper level tertiary (Master, Dr.)",
        "P" = "missing"),
       S = fct_recode(sostam,
         "1" = "Lowest, Bottom, 01",
         "2" = "02",
         "3" = "03",
         "4" = "04",
         "5" = "05",
         "6" = "06",
         "7" = "07",
         "8" = "08",
         "9" = "09",
         "10"= "Highest, Top, 10",
         "P" = "missing"),
       U = fct_recode(urbrum,
        "1" = "A big city",
        "2" = "The suburbs or outskirts of a big city",
        "3" = "A town or a small city",
        "4" = "A country village",
        "5" = "A farm or home in the country",
        "P" = "missing")
        )

#names(MCAdata1jh.dat)
#dim(MCAdata1jh.dat)
#MCAdata1jh.dat$E %>% levels()
#MCAdata1jh.dat$S %>% levels()
#MCAdata1jh.dat$U %>% levels()
#MCAdata1jh.dat$age_cat %>% levels()
#str(MCAdata1jh.dat$ga) # toimiikohan - chr-muuttuja? (16.10.20)

MCAdata1jh.dat <- MCAdata1jh.dat %>%
mutate(gaf = as_factor(ga))

#str(MCAdata1jh.dat$gaf)
#levels(MCAdata1jh.dat$gaf) # järjestyksellä ei liene väliä? (16.10.20)

# gaf ja ga: sama järjestys

MCAdata1jh.dat <- MCAdata1jh.dat %>%
       mutate(gaf = fct_relevel(gaf,
                                 "f1",
                                 "f2",
                                 "f3",
                                 "f4",
                                 "f5",
                                 "f6",
                                 "m1",
                                 "m2",
                                 "m3",
                                 "m4",
                                 "m5",
                                 "m6"))

# Lopuksi substanssimuuttutien nimet lyhyiksi

MCAdata1jh.dat <- MCAdata1jh.dat %>% mutate(a1 = Q1am,
                                            b1 = Q1bm,
                                            c1 = Q1cm,
                                            d1 = Q1dm,
                                            e1 = Q1em,
                                            a2 = Q2am,
                                            b2 = Q2bm)



# Tarkistustuksia datalle

# MCAdata1jh.dat %>% tableX (a1, Q1am)
# MCAdata1jh.dat %>% tableX (b1, Q1bm)
# MCAdata1jh.dat %>% tableX (c1, Q1cm)
# MCAdata1jh.dat %>% tableX (d1, Q1dm)
# MCAdata1jh.dat %>% tableX (e1, Q1em)
# MCAdata1jh.dat %>% tableX (a2, Q2am)
# MCAdata1jh.dat %>% tableX (b2, Q2bm)
# MCAdata1jh.dat %>% tableX(gaf, ga)

# Perustietoja - TÄSSÄ UUSI PDF-VIRHEILMOITUS 7.11.2020
# Ei tulosteta - kommentoidaan pois

#MCAdata1jh.dat %>% tableX (maa,a1, type = "row_perc")
#MCAdata1jh.dat %>% tableX (maa,b1, type = "row_perc")
#MCAdata1jh.dat %>% tableX (maa,c1, type = "row_perc")
#MCAdata1jh.dat %>% tableX (maa,d1, type = "row_perc")
#MCAdata1jh.dat %>% tableX (maa,e1, type = "row_perc")
#MCAdata1jh.dat %>% tableX (maa,a2,type = "row_perc")
#MCAdata1jh.dat %>% tableX (maa,b2,type = "row_perc")

#MCAdata1jh.dat %>% tableX(gaf, ga,type = "row_perc")
#MCAdata1jh.dat %>% tableX(maa, age_cat,type = "row_perc")
#MCAdata1jh.dat %>% tableX(maa, gaf,type = "row_perc")
#MCAdata1jh.dat %>% tableX(maa, S, type = "row_perc")
#MCAdata1jh.dat %>% tableX(maa, U, type = "row_perc")
#MCAdata1jh.dat %>% tableX(maa, E, type = "row_perc")


#Puuttuvien tietojen yleiskuva

# Puuttuvat tiedot aineistossa - viite datan dokumentointiin jossa taulukot.
# Vaihtelee maittain ja muuttujittain, paljon.

# Koko data (G1_1_data2.Rmd - skriptissä valitut muuttujat ja 25 maata)
#
#sum(!complete.cases(ISSP2012jh1d.dat)) = 9455
#dim(ISSP2012jh1d.dat) = 32823
#9455/32823 = 0.2880602

# Puuttuvat tiedot valitussa MCA-aineistossa

#missingMCAvars1 <-  c("Q1a","Q1b", "Q1c", "Q1d","Q1e","Q2a","Q2b","edu",
#                 "sosta", "urbru", "maa", "ika", "sp" )
#missingTestMCA1.dat <- ISSP2012jh1d.dat %>% select(all_of(missingMCAvars1))

#sum(!complete.cases(missingTestMCA1.dat)) = 6101
#dim(missingTestMCA1.dat) = 32823
#6101/32823 = 0.1858758 Puuttellisten havaintojen osuus.

#Pelkät kysymykset

#missingMCAvars2 <- c("Q1a","Q1b", "Q1c", "Q1d","Q1e","Q2a","Q2b")
#missingTestMCA2.dat <- ISSP2012jh1d.dat %>% select(all_of(missingMCAvars2))
#sum(!complete.cases(missingTestMCA2.dat))
# puuttuvia tietoja 4554
# 4553/32823 = 0.1387137


# Valitaan data

mcaDat11jh.dat <- MCAdata1jh.dat %>% select(a1,b1,c1, d1, e1,a2,b2)
# dim(mcaDat11jh.dat)

#glimpse(mcaDat11jh.dat)

Qmuuttujat1.mca <- mjca(mcaDat11jh.dat, ps="")

# ps="" muuttujan ja sen kategorian eroitinmerkki


par(cex = 0.6)
plot.mjca(Qmuuttujat1.mca, labels = c(1,2),
          main = "Symmetrinen kartta",
          sub = "Kysymykset Q1a, Q1b, Q1c, Q1d, Q1e, Q2a, Q2b, vastaukset S-s-?-e-E-P "
          )



par(cex=0.6)
plot.mjca(Qmuuttujat1.mca, what = c("all","all"),labels = c(0,2),
          col = c("lightblue", "red"),
           main = "Symmetrinen kartta",
          sub = "Kysymykset Q1a, Q1b, Q1c, Q1d, Q1e, Q2a, Q2b,vastaukset S-s-?-e-E-P, havainnot (n = 32 823)"
          )



#subsetcat viittaa muuttujan luokkien indeksiin

eiPvastaukset <- (1:42)[-c(6,12,18,24,30,36,42)]
# eiPvastaukset
#  puuttuva tieto on kuudes kategoria kaikilla kysymyksillä
# 1  2  3  4  5  7  8  9 10 11 13 14 15 16 17 19 20 21 22 23 25 26 27 28 29 31
# 32 33 34 35 37 38 39 40 41

#mcaDat11jh.dat[1:5,]

Qmuuttujat2.mca <- mjca(mcaDat11jh.dat, ps="", subsetcat=eiPvastaukset)



# subsetcat viittaa muuttujan luokkien indeksiin

eiPvastaukset <- (1:42)[-c(6,12,18,24,30,36,42)]

# eiPvastaukset
#  puuttuva tieto on kuudes kategora kaikilla kysymyksillä
# 1  2  3  4  5  7  8  9 10 11 13 14 15 16 17 19 20 21 22 23 25 26 27 28 29 31
# 32 33 34 35 37 38 39 40 41

# mcaDat11jh.dat[1:5,]

Qmuuttujat2.mca <- mjca(mcaDat11jh.dat, ps="", subsetcat=eiPvastaukset)

# Kontribuutiokartta on tarpeeksi selkeä, muutujien tunnukset erottuvat.
# Jätetään tämä kuva pois (25.11.20)
#
#plot.mjca(Qmuuttujat2.mca,
#          main="Seitsemän kysymystä, viisi vastausvaihtoehtoa",
#          sub = "subset: ei puuttuvien vastausten kategorioita(*P)")


# jätettään symmetrinen kartta pois, asymmetrinen on parempi (25.11.20)

plot.mjca(Qmuuttujat2.mca,
          what = c("all","all"),labels = c(0,2),
          col = c("lightblue", "red"),
          main="Seitsemän kysymystä, viisi vastausvaihtoehtoa",
          sub = "subset: ei puuttuvien vastausten kategoriaa (*P)")



plot.mjca(Qmuuttujat2.mca, map = "rowprincipal",
          what = c("all","all"),labels = c(0,2),
          col = c("lightblue", "red"),
          main="Asymmetrinen kartta - osajoukko: ei puuttuvia vastauksia",
          sub = "Kysymykset Q1a, Q1b, Q1c, Q1d, Q1e, Q2a, Q2b, vastaukset S-s-?-e-E")



# pois 25.11.2020
summary(Qmuuttujat2.mca)

# Pois 25.11.2020
Qmuuttujat2d3  <- mjca(mcaDat11jh.dat, ps="", nd = 3,subsetcat=eiPvastaukset)
summary(Qmuuttujat2d3)


knitr::include_graphics('img/CAquality.png')


knitr::include_graphics('img/BookdownProc.png')

# pois out.width='50%',


sessionInfo()


# echo = FALSE toistaiseksi.
#Testataan koodilohkojen listausta, näyttää toimivan mutta vaatii vielä säätämistä.
#Ohje löytyi [Yihui Xienin blogista](https://yihui.name/en/2018/09/code-appendix/)
#(luettu 26.10.2018).

Korrespondenssianalyysi - graafinen ja geometrinen data-analyysin menetelmä

Jussi Hirvonen

Versio 2.1, tulostettu 2020-11-29