Liite 1: Korrespondenssianalyysin teoriaa

Korrespondenssianalyysin perusyhtälöt ja kaavat

Perusyhtälöt on esitetty teoksen “Correspondece Analysis in Practice”(M. J. Greenacre 2017) liitteen “Theory of Correspondece Analysis” mukaisesti.

Datamatriisilla \(\boldsymbol{N}\) on \(I\) riviä ja \(J\) saraketta (\(I x J\)). Alkiot ovat ei-negatiivisia ja samassa mitta-asteikossa. Jos mitta-asteikko on intervalli- tai suhdeasteikko, mittayksiköiden on oltava samoja (esim. euroja, metrejä). Tietyin ehdoin myös negatiiviset luvut ovat sallittuja (LeRoux ja Rouanet 2004, 60).

Taulukon alkioiden summa on \(\sum_{i} \sum_{j}n_{ij} = n\), missä \(i = 1, \dots , I\) ja \(j = 1, \dots , J\).

Korrespondenssimatriisi \(\boldsymbol{P}\) saadaan jakamalla matriisin \(\boldsymbol{N}\) alkiot niiden summalla \(n\) .

Merkitään matriisin \(\boldsymbol{P}\) rivisummien vektoria \(\boldsymbol{r}\) (= \((r_{1}, \dots, r_{I})\)) ja sarakesummien vektoria \(\boldsymbol{c}\) (= \((c_{1}, \dots, c_{J})\)). Niitä vastaavat diagonaalimatriisit ovat \(\boldsymbol{D_r}\) ja \(\boldsymbol{D_c}\).

Matriisin transpoosi merkitään yläindeksillä \(T\), ja \(\boldsymbol{1}\) on sopivan dimension vektori, jonka alkiot ovat ykkösiä.

Korrespondenssianalyysin ratkaistaan singulaariarvohajotelman (singular value decomposition, SVD) avulla.

Singulaariarvohajotelma tuottaa ratkaisun, kun sitä sovelletaan standardoituun residuaalimatriisiin \(\boldsymbol{S}\).

\[\begin{equation} \boldsymbol{S} = \boldsymbol{D_r}^{-1/2}(\boldsymbol{P} - \boldsymbol{r}\boldsymbol{c}^T)\boldsymbol{D_c}^{-1/2} . \tag{8.1} \end{equation}\]

Residuaalimatriisi voidaan esittää myös ns. kontingenssi-suhdelukujen (contingency ratio) avulla kahdella tavalla.

\[\begin{equation} \boldsymbol{D_r}^{-1} \boldsymbol{P} \boldsymbol{D_c}^{-1} = \left( \frac{p_{ij}} {r_{i} c{j}} \right) , \tag{8.2} \end{equation}\]

\[\begin{equation} \boldsymbol{S} = \boldsymbol{D_r}^{1/2} (\boldsymbol{D_r}^{-1} \boldsymbol{P} \boldsymbol{D_c}^{-1} - \boldsymbol{1}\boldsymbol{1}^{T} ) \boldsymbol{D_c}^{-1/2} \;\;\; . \tag{8.3} \end{equation}\]

Toinen esitystapa on hyödyllinen, kun tarkastellaan CA:n yhteyksiä muihin läheisiin menetelmiin. Näitä ovat esimerkiksi “suhteellisten osuuksien datan” analyysi (log ratio analysis of compositiona data), moniulotteinen skaalaus, lineaarinen diskriminanttianalyysi, kanoninen korrelaatioanalyysi, pääkomponenttianalyysi, kaksoiskuvat ja muut SVD-hajotelmaan perustuvat dimensioiden vähentämisen menetelmät.

Samat kaavat voi esittää myös alkiomuodossa:

\[\begin{equation} s_{ij} = \frac{p_{ij}-r_{i}c_{j}} { \sqrt{r_{i}c_{j} } } , \tag{8.4} \end{equation}\]

\[\begin{equation} s_{ij} = \sqrt{r_{i}} \left( \frac{p_{ij}}{r_{i}c_{j}} \right) \sqrt{c_{j}} \;\;\; . \tag{8.5} \end{equation}\]

Alkiomuodossa esitetyistä kaavoista näkee rivi- ja sarakeratkaisujen sidoksen. Ratkaisujen duaalisuus on teoreettinen tulos, jonka voi perustella täsmällisesti algebrallisen geometrian avulla. Käytännössä rivi- ja sarakeongelman duaalisuus tarkoittaa sitä, että vain toinen ongelma on ratkaistava.

Singulaariarvohajotelma matriisille \(\boldsymbol{S}\) on

\[\begin{equation} \boldsymbol{S} = \boldsymbol{U} \boldsymbol{D_{\alpha}} \boldsymbol{V}^{T} , \tag{8.6} \end{equation}\]

missä \(\boldsymbol{D_{\alpha}}\) on diagonaalimatriisi, jonka alkiot ovat singulaariarvot suuruusjärjestyksessä \(\alpha_{1}\geq \alpha_{1} \geq \cdots\).

Matriisit \(\boldsymbol{U}\) ja \(\boldsymbol{V}\) ovat ortogonaalisia singulaarivektoreiden matriiseja. Singulaariarvohajotelman merkitys dimensioiden vähentämiselle perustuu Eckart - Young - teoreemaan. Teoreema kertoo että saamme pienimmän neliösumman \(m\) - ulotteisen approksimaation matriisille \(\boldsymbol{S}\) matriisien \(\boldsymbol{U}\) ja \(\boldsymbol{V}\) ensimmäisten sarakkeiden ja ensimmäisten singulaariarvojen avulla.

\[\begin{equation} \boldsymbol{S}_{(m)} = \boldsymbol{U}_{(m)} \boldsymbol{D}_{\alpha(m)} \boldsymbol{V}_{(m)}^{T} \tag{8.7} \end{equation}\]

Korrespondenssianalyysin ratkaisualgoritmissa tätä tulosta on muokattava niin, että rivien ja sarakkeiden massat huomioidaan pienimmän neliösumman approksimaatiossa painoina.

Näin saadaan standardikoordinaatit ja pääkoordinaatit riveille ja sarakkeille.

Rivien standardikoordinaatit

\[\begin{equation} \boldsymbol{\Phi} = \boldsymbol{D_r}^{-\frac{1}{2}} \boldsymbol{U} \tag{8.8} \end{equation}\]

Sarakkeiden standardikoordinaatit

\[\begin{equation} \boldsymbol{\Gamma} = \boldsymbol{D_c}^{-\frac{1}{2}} \boldsymbol{V} \tag{8.9} \end{equation}\]

Rivien pääkoordinaatit

\[\begin{equation} \boldsymbol{F} = \boldsymbol{D_r}^{-\frac{1}{2}} \boldsymbol{U} \boldsymbol{D_{\alpha}} = \boldsymbol{\Phi} \boldsymbol{D_{\alpha}} \tag{8.10} \end{equation}\]

Sarakkeiden pääkoordinaatit \[\begin{equation} \boldsymbol{G} = \boldsymbol{D_c}^{-\frac{1}{2}} \boldsymbol{V} \boldsymbol{D_{\alpha}} = \boldsymbol{\Gamma} \boldsymbol{D_{\alpha}} \tag{8.11} \end{equation}\]

Pääakseleiden inertiat (principal inertias) \(\lambda_{k}\)

\[\begin{equation} \lambda_{k} = \alpha_{k}^2, \: k = 1,\dots,K, K = min \{ I-1, J-1 \} \end{equation}\]

Ratkaisun dimensio on myös maksimi-inertia. Tässä aineistossa ja vastaavissa kyselytutkimusdatoissa inertia on yleensä paljon maksimia pienempi. Asymmetrisissä kartoissa ideaalipisteet ovat kaukana origon lähelle pakkautuneesta havaintojen pilvestä.

Korrespondenssianalyysi ratkaisun akseleiden inertioita kutsutaan usein ominaisarvoiksi, mutta periaatteessa SVD-ratkaisulla saadaan singulaariarvot. Niiden neliöt ovat akseleiden inertioita. Ominaisarvojen ja singulaariarvojen yhteys on läheinen ja riippuu diagonalisoitavan matriisin ominaisuuksista. Termiä “vektori” käytetään kartoista puhuttaessa, kun viitataan esimerkiksi origosta sarakepisteeseen piirrettyyn nuoleen. Myös janan synonyyminä käytetään yleisesti termiä vektori (kts. esim. (M. Greenacre 2013)).

Korrespondenssimatriisi \(\boldsymbol{P}\) voidaan esittää matriisi- ja alkiomuodossa ns. palautuskaavana (reconstitution formula).

\[\begin{equation} \boldsymbol{P} = \boldsymbol{D}_{r} \left( \boldsymbol{1}\boldsymbol{1}^{T} + \boldsymbol{\Phi}\boldsymbol{D}_{\lambda}^{\frac {1}{2}}\boldsymbol{\Gamma}^{T}\right)\boldsymbol{D}_{c} \tag{8.12} \end{equation}\]

\[\begin{equation} p_ {ij}= r_{i}c_{j} \left(1 + \sum_{k=1}^{K} \sqrt{\lambda_{k}} \phi_{ik} \gamma_{jk} \right) \tag{8.13} \end{equation}\]

Rivien ja sarakkeiden riippuvuutta kuvaavat transitioyhtälöt (transition equations).

Pääkoordinaatit standardikoordinaattien funktiona (barysentrinen ominaisuus, barycentric relationships):

\[\begin{equation} \boldsymbol{F} = \boldsymbol{D}_{r}^{-1} \boldsymbol{P}\boldsymbol{\Gamma} \tag{8.14} \end{equation}\]

\[\begin{equation} \boldsymbol{G} = \boldsymbol{D}_{c}^{-1} \boldsymbol{P}^{T}\boldsymbol{\Phi} \tag{8.15} \end{equation}\]

Pääkoordinaatit pääkoordinaattien funktiona:

\[\begin{equation} \boldsymbol{F} = \boldsymbol{D}_{r}^{-1} \boldsymbol{P}\boldsymbol{G}\boldsymbol{D}_{\lambda}^{-\frac{1}{2}} \tag{8.16} \end{equation}\]

\[\begin{equation} \boldsymbol{G} = \boldsymbol{D}_{c}^{-1} \boldsymbol{P}^{T}\boldsymbol{F}\boldsymbol{D}_{\lambda}^{-\frac{1}{2}} \tag{8.17} \end{equation}\]

Yhtälöt (8.14) ja (8.14) esittävät profiilipisteet ideaalipisteiden (vertex points) painotettuina keskiarvoina, painoina profiilin elementit. Asymmetriset kartat (rivien tai sarakkeiden suhteen) perustuvat näihin yhtälöihin. Yhtälöiden (8.16) ja (8.17) kahdet pääkoordinaatit ovat perusta symmetrisille kartoille. Myös niitä yhdistää barysentrinen painotetun keskiarvon riippuvuus, mutta mukana ovat skaalaustekijät \(\frac{1}{\sqrt{\lambda_{i}}}\).

Pisteet ja projektio aliavaruuteen

Kuva on kurssimateriaaleista (M. Greenacre 2017).

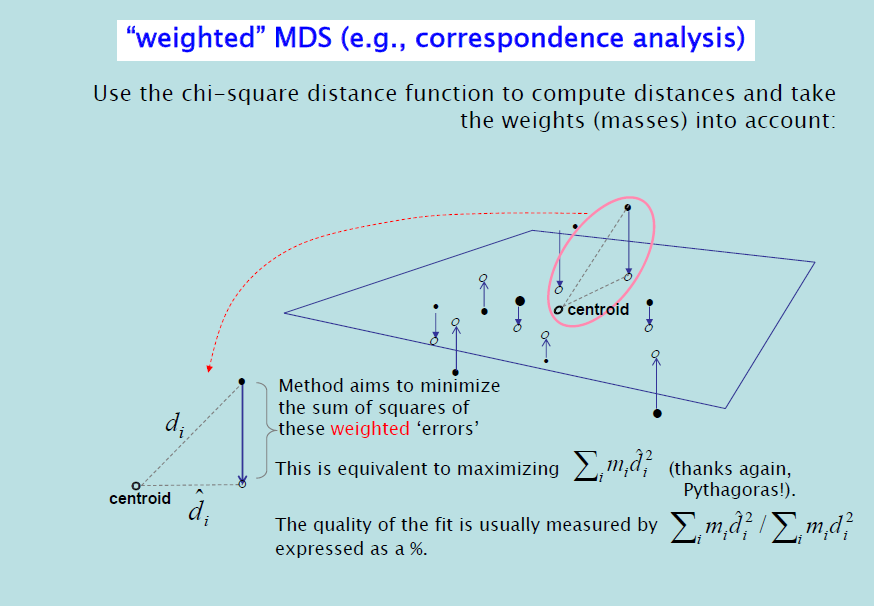
Kuva 8.1: Pisteen projektio aliavaruuteen

Kuvassa on esitetty korrespondenssianalyysin ratkaisun minimointiongelma. Pisteen projektio on sitä parempi mitä pienempi kulma on sentroidista pisteeseen piirretyn janan ja pisteen projektion välillä. cor-tunnusluku ca-funktion numeerisissa tuloksissa tämän kulman kosinin neliö. Pisteen kuvauksen laatu (qlt) ca-tuloksissa on valitun approksimaation akseleiden kvaliteettien (cor) summa.

Kuvasta voi myös hahmottaa sen periaatteen, että projektiossa kaukana olevat pisteet ovat kaukana myös alkuperäisessä avaruudessa. Projektiossa lähekkäin olevat pisteet voivat olla alkuperäisessä avaruudessa kaukana toisistaan, jos niiden projektion laatu on huono.

Monimuuttujakorrespondenssianalyysi MCA

Usean muuttujan korrespondenssianalyysissä tutkitaan usean muuttujan välisiä yhteyksiä. Kartan tulkinnan apuna siihen voidaan lisätä havaintojen sijaan niiden keskiarvopisteitä ja niille simuloituja luottamusellipsejä. Kuvien pääongelma on liian suuri määrä pisteitä, ja analyysin tavoite on usein mahdollisimman yksinkertainen kartta.

Usean muuttujan analyysissä kohteena on joko indikaattorimatriisi \(\boldsymbol{Z}\) tai Burtin matriisi \(\boldsymbol{B}\)

Indikaattorimatriisissa rivit ovat havaintoja ja sarakkeet luokittelumuuttujan arvoja. Havaintoa vastaa rivi nollia ja 1 valitun vastausvaihtoehdon kohdalla. Tästä seuraa, että vain erilaiset vastaukset määrittävät rivien etäisyyksiä.

Burtin matriisi on erikoistapaus yhdistetyistä matriiseista. Siihen on koottu kaikki tutkittavien muuttujien pareittain muodostetut taulukot. Diagonaalilla ovat muuttujien ristiintaulukoinnit itsensä kanssa. Ratkaisu riippuu vain näistä parittaisista taulukoista. Burtin matriisi on kätevä välivaihe matriisien yhdistelyssä.

Molemmat matriisit paisuttavat keinotekoisesti kokonaisinertiaa, ja esimerkiksi kaksiulotteisen kartan selitetyn inertian osuudet jäävät melko pieniksi. Ratkaisuna on inertian oikaisu tai korjaus (adjusted inertia), jossa mm. poistetaan kokonaisinertialaskelmista Burtin matriisin diagonaalilla olevat alimatriisit. Näillä korjauksilla ei ole vaikutusta kartan pisteiden sijaintiin. Tämä menetelmä on ca-paketin mjca-funktion oletus.

Kolmas vaihtoehto on ns. yhdistetty korrespondenssianalyysi (joint ca).

Greenacre on kirjoittanut useissa yhteyksissä MCA:n geometrisen tulkinnan ongelmista. Greenacre ja Hastie (1987) (s. 447) sanovat asian näin:“Finally, although we have motivated simple correspondence analysis from the geometric point of view, the geometry of the indicator matrix in multiple correspondence analysis is admittedly not convincing. Distances between the row profiles of an indicator matrix and projections of articficial column vertices have less intuitive appeal. However, the scaling interpretation remains attractive in this case; the displays are graphical representations of optimal scale values for the categories.”

Greenacre jatkaa samasta aiheesta artikkelikokoelmassa (M. Greenacre ja Blasius 2006 , s. 41, s. 61): “Yleistys useammalle kuin kahdelle muuttujalle ei ole ilmeinen eikä hyvin määritelty”. Silti MCA onnistuu esittämään hyvin kiinnostavia yhteyksiä muuttujien välillä (“succesfully recovers interesting patterns of association”). Kriittisyys ei kuitenkaan estä häntä soveltamasta MCA-analyysiä. Tulkitsen tämän niin, että menetelmää voi aivan hyvin soveltaa, mutta geometrista tulkintaa ei voi suoraan siirtää CA-kartoista MCA-karttoihin. Greenacre esittelee perusteellisesti MCA-sovelluksia kaksoiskuvia käsittelevässä kirjassaan (Greenacre 2010). Ehkä korrespondenssianalyysin matemaattinen teoria ei ole vielä täysin valmis?