Luku 4 Täydentävät pisteet
Edellisessä luvussa kuviin listättiin informaatiota värisävyinä (kontribuutiot) ja rivi- ja sarakepisteiden kokoa muuntelemalla (massat). Täydentävät pisteet (supplementary points,CAiP s. 89-) ovat rivejä tai sarakkeita, jotka lisätään karttaan. Mikä tahansa rivi tai sarake voidaan lisätä kuvaan, jos se on järkevästi vertailukelpoinen kartan määrittäneiden profiilien kanssa.
Tällainen piste on kartan laskennassa passiivinen, sillä on sijainti kartalla mutta ei massaa eikä vaikutusta inertiaan. Passiivisilla pisteillä ei ole vaikutusta (kontribuutiota) kartan pääakseleihin.
Täydentävillä pisteillä on kolme yleistä käyttötarkoitusta. Kartalle voidaan lisätä profiili, joka on jollain lailla sisällöllisesti erilainen kuin muut. Esimerkkiaineistossa kartalle voisi lisätä joitain Euroopan ulkopuolisia maita. Vaikka nämä riviprofiilit eivät vaikuta kartan akseleiden määräytymiseen, ne voidaan esittää kuuden maan määrittämässä “avaruudessa”. Projektion laatu (suhteelliset kontribuutiot) voidaan myös esittää.
Toinen käyttötapaus on pienen massan profiili. Tällaisella pisteellä voi olla iso vaikutus ratkaisuun, mutta passiivisena pisteenä se sijoitetaan muiden pisteiden määrittämälle kartalle. Jo sisällöllisistä syistä pienen massan pisteiden esitystä kannattaa harkita, ne sijaitsevat kaukana origosta ja huonontavat kuvan laatua.
Kolmas mahdollisuus on jakaa pistejoukkoja osajoukkoihin ja esittää niiden summaprofiili täydentävänä pisteenä. Summaprofiili on osiensa painotettu (barysentrinen) keskiarvo. Kun se esitetään passiivisena pisteenä, havaintoja ei oteta ratkaisuun kahta kertaa. Profiilien yhdistämiseen liittyy korrespondenssianalyysin tärkein ominaisuus, jakaumaekvivalenssi (distributional equivalence). Se on ollut menetelmän kehittämisen tärkein tavoiteltu ominaisuus. Profiileiltaan samanlaiset rivit voidaan yhdistää, analyysin tulokset eivät muutu. Khii2-etäisyysmitta on ainoa etäisyysmitta, joka toteuttaa tämän periaatteen.
LeRoux ja Rouanet (2004) esittelevät menetelmän matemaattiset perusteet ja jakaumaekvivalenssin perusteellisesti. Havainnollinen esitys löytyy Greenacren oppikirjasta (CAiP).
Täydentävien profiilien lisääminen vaatii jo yksinkertaisia matriisioperaatioita. Korrespondenssianalyysi on käytännössä matriisien muokkausta tutkimusongelman tarpeisiin.
4.1 Saksan ja Belgian alueet
Saksan ja Belgian aineistossa on mukana aluejako: entiset Itä- ja Länsi-Saksa (dE,dW), Flanderi (bF), Vallonia (bW) ja Bryssel (bB).
| S | s | ? | e | E | Total | |
|---|---|---|---|---|---|---|
| bF | 5.04 | 23.81 | 25.89 | 30.83 | 14.43 | 100.00 |
| bW | 10.82 | 21.02 | 18.57 | 24.08 | 25.51 | 100.00 |
| bB | 17.03 | 20.94 | 16.63 | 23.87 | 21.53 | 100.00 |
| BG | 12.81 | 42.89 | 22.26 | 20.63 | 1.41 | 100.00 |
| dW | 11.40 | 26.82 | 11.83 | 32.13 | 17.82 | 100.00 |
| dE | 5.85 | 11.33 | 10.97 | 29.80 | 42.05 | 100.00 |
| DK | 5.04 | 17.15 | 10.95 | 16.71 | 50.14 | 100.00 |
| FI | 4.23 | 16.94 | 13.42 | 38.11 | 27.30 | 100.00 |
| HU | 21.97 | 28.89 | 22.57 | 19.06 | 7.52 | 100.00 |
| All | 9.95 | 23.76 | 16.79 | 26.10 | 23.41 | 100.00 |
Aineistoon lisätään passiiviisina riveinä Saksan ja Belgian maaprofiilit (DE, BE). Maiden massoja ei skaalata yhtä suuriksi, otoskoot vaikuttavat ratkaisuun.
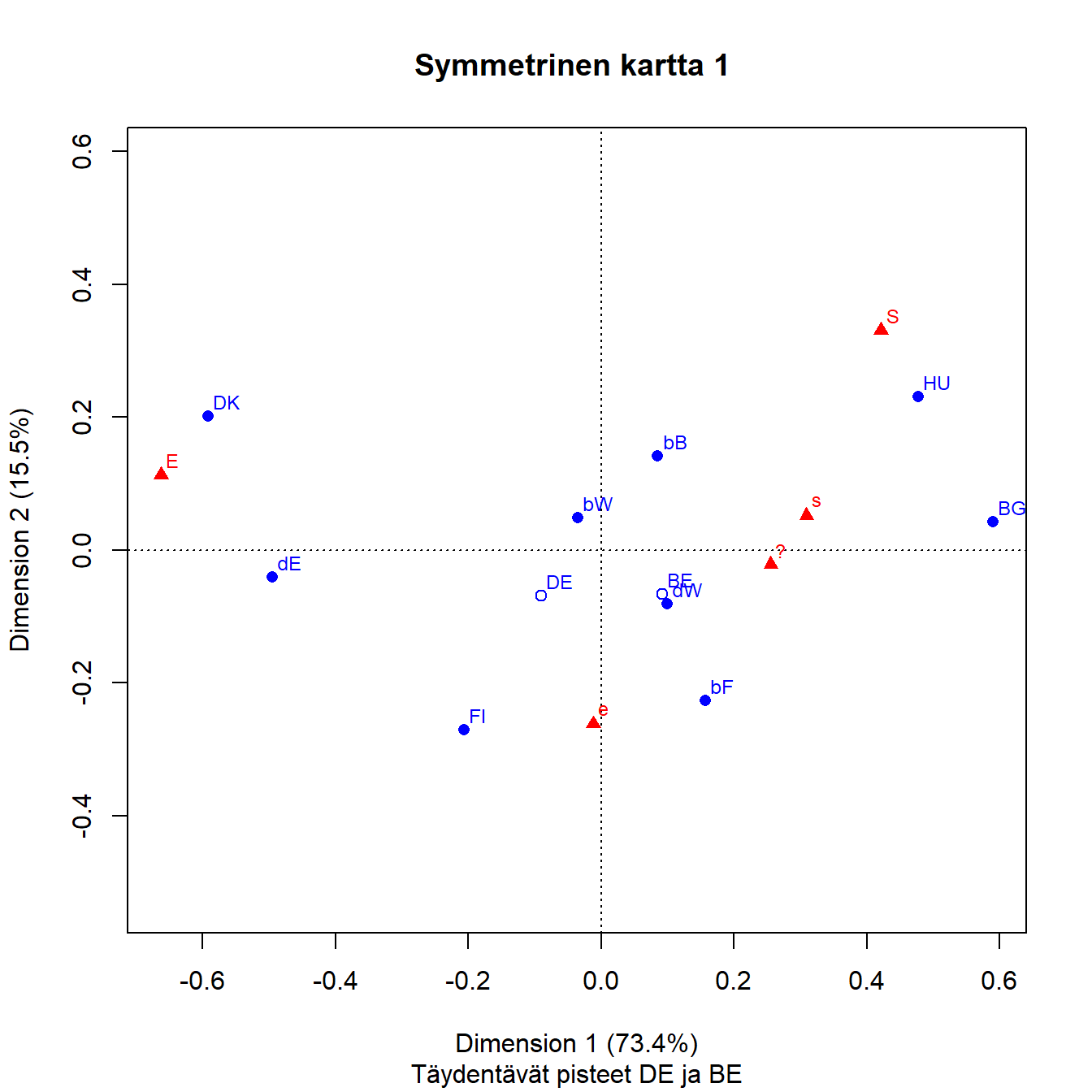
Kuva 4.1: Q1b: Saksan ja Belgian aluejako
Saksan ja Belgian täydentävät pisteet ovat osiensa barysentrisiä keskiarvoja, etäisyys on sitä pienempi mitä suurempi on osuus. Saksan piste sijaitsee siksi lähempänä Länsi-Saksan pistettä. Jos karttaa vertaa kuvaan 3.3 ei eroja juuri ole. Saksan ja Belgian osien sijoittuminen on kiinnostava. Itäinen Saksa on selvästi liberaalilla puolella, ensimmäisellä dimensiolla lähinnä Tanskaa. Läntinen Saksa on ensimmäisellä dimensiolla konservatiivisella puolella Belgian maapisteen tasolla. Belgian alueista Vallonia (bW) on liberaalilla puolella mutta kaikkein eniten oikealla. Bryssel ja Flanderi ovat konservatiivisella puolella, toinen Länsi-Saksaa liberaalimpi ja toinen konservatiivisempi. Belgian osat hajoavat toiseen suuntaan kuin Saksan, liberaalein Flanderi on myös kaikkein maltillisin ja Bryssel vastaavasti tiukempien mielipiteiden puolella. Sarakepisteiden suhteelliset sijainnit toisiinsa nähden eivät oleellisesti muutu.
Bryssel ja Vallonia näyttävä olevan hyvin lievästi U-muotoisen maapisteiden parven sisällä. Tämä kaariefekti tai Guttman-efekti on kartoissa yleinen. Se on tavallaan ratkaisun geometriasta. Rivipisteiden pilvi on sarakkeiden ideaalipisteiden virittämän verteksin sisällä, ja ainoa reitti verteksin kulmasta toiseen kulkee tasolla kaarevasti (CAiP, s. 127). Voi myös sanoa, että kaariefektin taustalla on järjestysasteikon muuttujan korrelaatio ((LeRoux ja Rouanet 2004), s. 220). Kaaren sisäpisteet ovat usein polarisoituneita ensimmäisen dimension “ääripäävastausten” välillä. Tässä vaikutus on heikko, taulukossa 4.1 ei mitään selvää polarisaatiota näy.
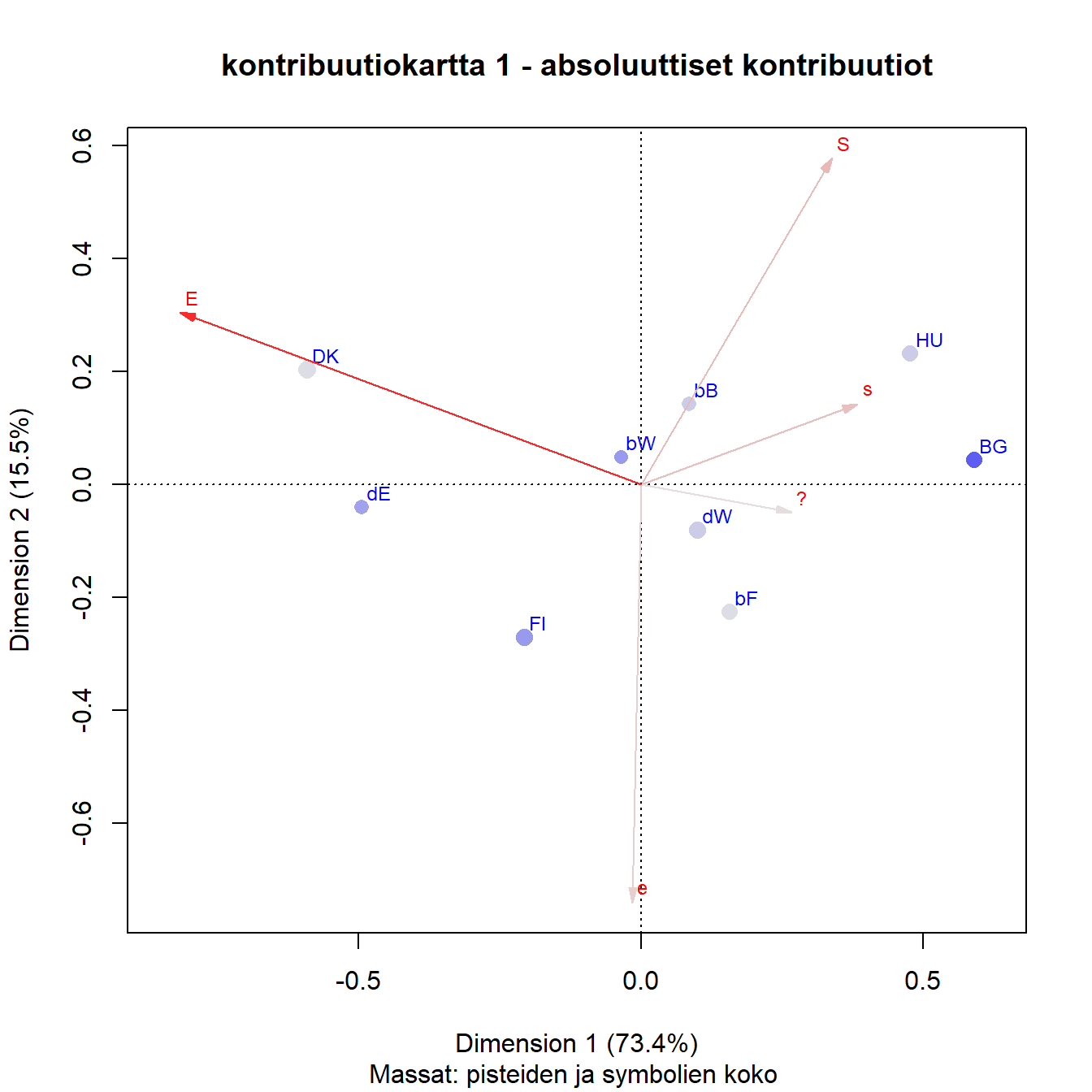
Kuva 4.2: Q1b: Saksan ja Belgian aluejako
Kontribuutiokartasta täydentävät pisteet on jätetty pois, ne eivät vaikuta ratkaisuun. Saksan ja Belgian osien massat ovat tietenkin pienempiä.
Sarakkeiden kontribuutiot ovat samantapaiset kuin alkuperäisessä kartassa 3.6. Rivipisteiden kontribuutioista osa on selvästi pienempiä, erityisesti Länsi-Saksa kaksi Belgian aluetta (bB, bF). Kuvan perusteella ei voi sanoa johtuuko tämä pelkästään massojen pienentymisestä.
Unkarin ja Bulgarian kontribuutiot muuttuvat eri suuntiin, Unkarin pienenee ja Bulgarian kasvaa.
4.2 Korrespondenssianalyysin numeeriset tulokset
Korrespondenssianalyysin numeeriset tulokset ovat tärkeitä tulkinnan varmistamiselle ja antavat tarkemman kuvan ratkaisusta. Nämä tulokset ovat erilaisia kokonaisinertian dekomponointeja. Kokonaisinertia (total inertia) profiilien ja keskiarvoprofiilin khii2-etäisyyksien massoilla painotettu summa (kaava (3.6)). Se kuvaa profiilipisteiden hajontaa ideaalipisteiden verteksin sisällä. Maksimi-inertia saavutetaan kun profiilit ovat verteksien kärkipisteissä, jokaisessa profiilissa on vain yksi luokittelumuuttujan arvo. Inertia on sama kuin ratkaisun dimensio, tässä esimerkissä 4 (sarakkeiden lukumäärä - 1). Numeeristen tulosten esittelyn tärkein lähde on CAiP, luku 11 ja liite B.
R-paketti “ca” listaa numeeriset tulokset suppeasti (print) ja laajemmin (summary). Alla on laajempi tulostus tutkielman esimerkin tilanteesta.
Ensimmäisenä on listattu kokonaisinertia pääakseleittain. Tässä suhteelliset luvut on esitetty prosentteina. Muut luvut on luettavuuden vuoksi skaalattu, joko kerrottu tuhannella tai esitetty “permills” (summa on 1000).
##
## Principal inertias (eigenvalues):
##
## dim value % cum% scree plot
## 1 0.154101 73.4 73.4 ******************
## 2 0.032489 15.5 88.9 ****
## 3 0.014294 6.8 95.7 **
## 4 0.008944 4.3 100.0 *
## -------- -----
## Total: 0.209828 100.0
##
##
## Rows:
## name mass qlt inr k=1 cor ctr k=2 cor ctr
## 1 | bF | 124 650 69 | 157 212 20 | -226 438 195 |
## 2 | bW | 60 388 3 | -36 137 0 | 48 252 4 |
## 3 | bB | 63 481 17 | 85 127 3 | 142 354 39 |
## 4 | BG | 113 878 215 | 590 874 255 | 43 5 6 |
## 5 | dW | 143 345 33 | 100 208 9 | -81 138 29 |
## 6 | dE | 67 966 82 | -495 960 107 | -41 7 3 |
## 7 | DK | 170 971 327 | -591 869 387 | 202 102 214 |
## 8 | FI | 136 957 79 | -206 352 38 | -271 605 307 |
## 9 | HU | 122 927 177 | 477 751 181 | 231 176 201 |
## 10 | (*)BE | <NA> 512 <NA> | 92 338 <NA> | -66 173 <NA> |
## 11 | (*)DE | <NA> 418 <NA> | -90 265 <NA> | -68 153 <NA> |
##
## Columns:
## name mass qlt inr k=1 cor ctr k=2 cor ctr
## 1 | S | 99 816 167 | 421 505 115 | 331 311 335 |
## 2 | s | 238 781 143 | 309 759 147 | 52 22 20 |
## 3 | | 168 594 88 | 255 589 71 | -22 4 2 |
## 4 | e | 261 871 98 | -12 2 0 | -262 870 550 |
## 5 | E | 234 999 505 | -663 971 667 | 113 28 93 |Rivi- ja sarakeprofiileista esitetään samat tiedot. Ensimmäisessä kolmen sarakkeen joukossa kerrotaan pisteen massa, laatu (qlt) ja inertiakontribuutio.
Inertiakontribuutio (inr) on suhteellinen osuus kokonaisinertiasta. Aktiivisia rivejä on 9, joten tasaisesti jaettu inertia olisi noin 110. Tanska, Bulgaria ja Unkari “selittävät” suurimman osan inertiasta. Belgian ja Saksan alueiden kontribuutiot ovat pieniä. Nämä inertiaosuudet ovat osuuksia kokonaisinertiasta alkuperäisessä neljässä ulottuvuudessa.
Laatu kertoo, miten hyvin piste on esitetty kartalla, miten suuri osa sen inertiasta on esitetty kartalla. Pisteen inertia on sen massalla painotettu poikkeama aineiston keskiarvosta, ja jos tämä poikkeama saadaan kartassa näkymään piste on esitetty hyvin.
Kaksiulotteinen kartta, kuten tässä, on yleisin valinta, laatu kerrotaan valitulle dimensioiden määrälle. Laatu ei riipu massasta, vaan pisteen ja kartan akseleiden välisistä kulmista (kts. teorialiite). Saksan osien ero laadussa on iso, Itä-Saksalla se on erittäin hyvä ja Länsi-Saksalla huono. Belgian alueista Vallonia on huonoimmin esitetty, ja vain Flanderin laatu on kohtuullisen hyvä. Kovin hyvä ei ole täydentävien maapisteidenkään laatu.
Kaksi seuraavaa kolmen sarakkeen ryhmää kertovat tulokset valituille dimensioille eli ratkaisulle. Molempien dimensioiden (“k=1”, “k=2”) pääkoordinaattien (x 1000) lisäksi raportoidaan dimension suhteellinen kontribuutio pisteen inertiaan (“cor”). Nämä tunnusluvut summautuvat laaduksi (qlt), ja ne voidaan tulkita korrelaation neliöiksi (kts. teorialiite).
Erityisesti Belgian alueiden projektion laatu on huonompi ensimmäisellä dimensiolla. Itä-Saksa ja Bulgaria taas ovat hyvin esitettyjä vain ensimmäisellä dimensiolla eivätkä juuri ollenkaan korreloi toisen dimension kanssa.
Pisteen absoluuttinen kontribuutio kertoo sen osuuden dimension inertiasta (summa 1000). E-sarake “selittää” ensimmäisen dimension inertiasta noin 66 prosenttia, ja dimensio saman verran kokonaisinertiasta. Absoluuttinen kontribuutio riippuu massasta ja siitä paljonko piste poikkeaa koko aineiston keskiarvopisteestä.
Numeerisista tuloksista voidaan varmistaa akseleiden tulkinta sarakkeiden avulla. Sarakkeet ovat hyvin esitettyjä tasossa, ainoastaan neutraali vaihtoehto on heikommin kuvattu, mutta sillä ei ollut roolia tulkinnassa.
E-sarakkeen vaikutuksen suunta ensimmäisellä dimensiolla näkyy pääkoordinaatin etumerkistä (k1 = -663), ja sen kontrastina ovat S- ja s- sarakkeet positiiviseen suuntaan. Toinen dimensio on kontrasti S- ja e-sarakkeiden välillä ja ne selittävät akselin inertian. Kaikki tämä voitiin päätellä kuvasta, ja numeeriset tulokset vahvistavat tulkinnan. Sarake S on ainoa, jonka kontribuutio on merkittävä molemmille dimensioille.
Jos pisteen kontribuutio akselille on iso, akselin suhteellinen kontribuutio (cor) pisteen inertiaan on suuri. Kääntäen tämä ei päde, piste voi olla akselilla hyvin esitetty mutta kontribuutio on silti pieni.
4.3 Esimerkki kolmiulotteisesta kartasta
Belgian ja Länsi-Saksan pisteet on esitetty huonosti kaksiulotteisella kartalla. Kolmiulotteinen ratkaisu näyttää miten ne sijoittuvat kolmannen akselin suunnassa. Tässä tarkastelu on vain diagnostiikkaa. Toisenlainen esimerkki on tutkimus Ranskan politiikan dimensiosta (“French political space”) 1990-luvun lopulla (LeRoux ja Rouanet 2004, 365). Siinä Ranskan poliittiset puolueet sijoitetaan kolmelle sisällöllisesti perustellulle dimensiolle.
Kolmannen dimension hajonnan voi esittää kahtena karttana.
Ensimmäisen ja kolmannen dimension kuvassa (Kuva 4.3) näkyy pisteparven hajonta tärkeimmän dimension ympärillä. Sarakepisteiden järjestys säilyy samana, samoin maapisteiden oikealta vasemmalle. Kaikki pisteet paitsi Vallonia hajoavat kolmannen akselin suuntaan. Belgian kahden pisteen (bB ja bF) eron havaitsee helposti, samoin Unkarin ja Bulgarian.
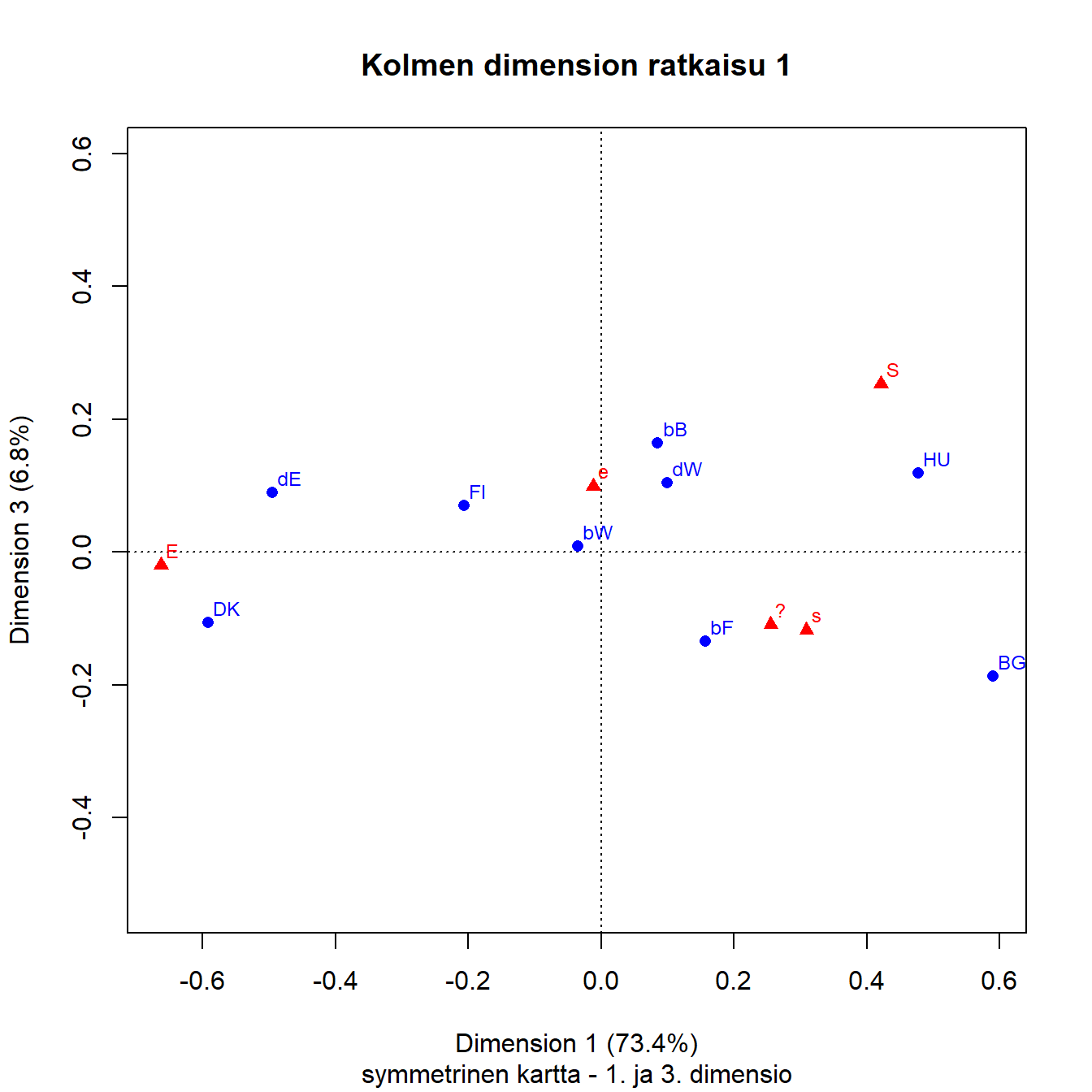
Kuva 4.3: Q1b: Saksan ja Belgian aluejako
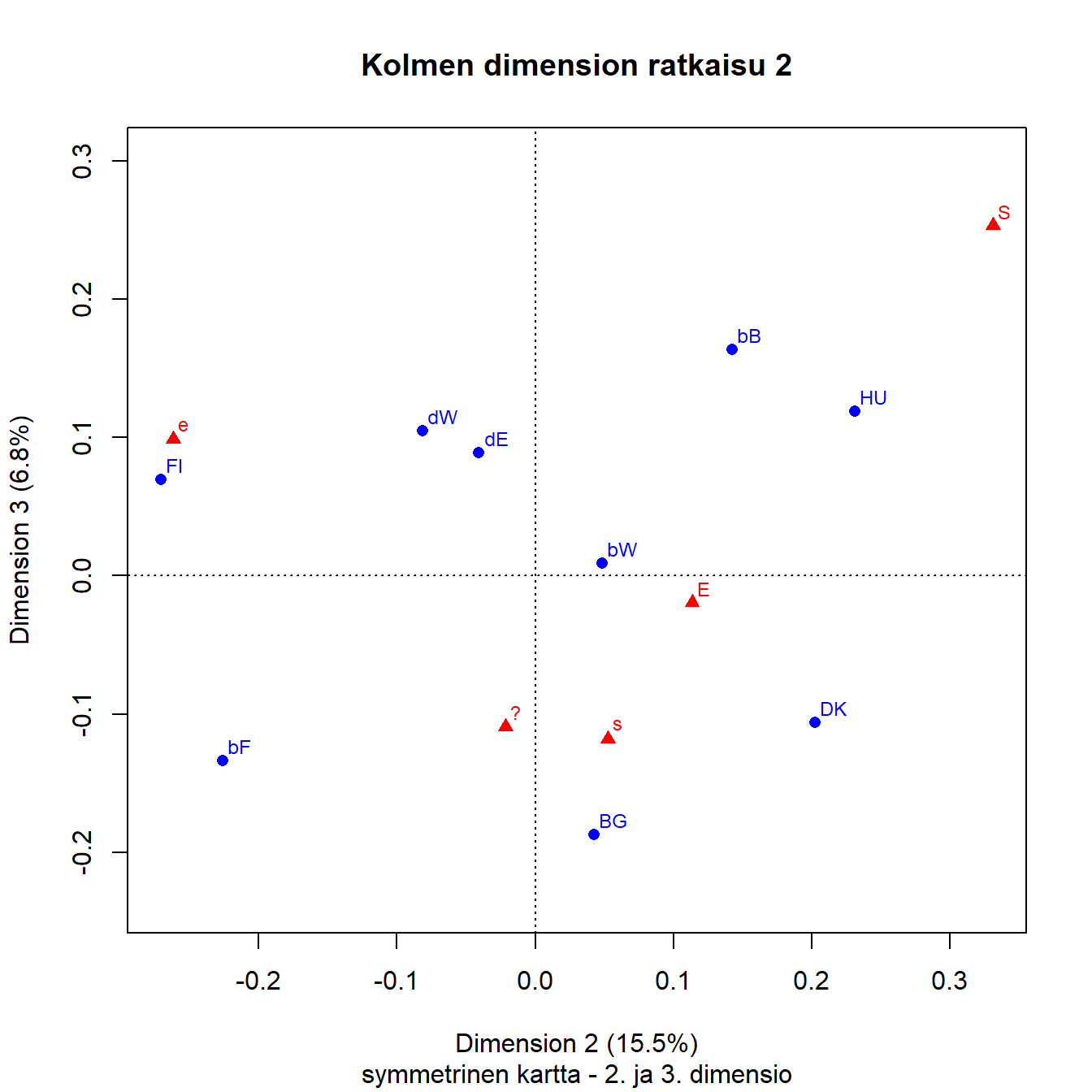
Kuva 4.4: Q1b: Saksan ja Belgian aluejako
Toisen ja kolmannen dimension kartalla (Kuva 4.4) on esitetty noin viidesosa kokonaisinertiasta. Tässäkin kuvassa Brysselin (bB) ja Unkarin pisteet ovat kontrastina Flanderin, Bulgarian ja Tanskan pisteille.
Diagnostisessa tarkastelussa on helpompaa käyttää dynaamisia kolmiulotteisia kuvia. R-ympäristössä saa grafiikkaikkunaan tulostettua kolmiulotteisen kuvan, jota voi käännellä ja katsoa eri kulmista. Näin saa paljon helpommin käsityksen kolmannen dimension hajonnasta.
Tässä on tyydyttävä kahteen kuvakaappaukseen (ks. alla kuvat 4.5 ja 4.6).
Kuva 4.5: Saksan ja Belgian aluejako - 3d-kuva1
Kuva 4.6: Saksan ja Belgian aluejako - 3d-kuva2
Miten kaksiulotteisessa kartassa huonosti esitettyjen pisteiden analyysiä voisi jatkaa? Siihen nämä kartat eivät suoraan anna mitään vastausta. Vaihtoehtoisia tapoja esitellään seuraavissa luvuissa.