Luku 5 Yhteisvaikutusmuuttujat
Yksinkertaisin tapa tutkia taustamuuttujien yhteisvaikutuksia on yhdistää kaksi muuttujaa uudeksi luokittelumuuttujaksi (“interactive coding”). Miehet ja naiset on seuraavaksi luokiteltu kuuteen ikäluokkaan (1=15-25, 2 =26-35, 3=36-45, 4=46-55, 5=56-65, 6= 66 tai vanhempi).
Poikkileikkausaineistossa vastaajan ikä kertoo myös ikäluokan (kohortin). Vastaajat ovat kokeneet kaksi suurta mullistusten vuotta elämänsä eri vaiheissa. Kaksi nuorinta ikäluokkaa on ollut 1990 alle 14-vuotiaita ja vanhin ikäluokka yli 44-vuotiaita. Finanssikriisin vuonna 2008 toiseksi nuorin ikäluokka on ollut 22-31 vuotiaita, ja kaksi vanhinta yli 51-vuotiaita. Pelkän ikävaikutuksen analyysi edellyttäisi vähintään kahden aineiston yhdistämistä.
Kolmen muuttujan yhteisvaikutusmuuttajaan yhdistän vastaajan maan. myös maa. Käytännössä kolmen luokittelumuuttujan yhdistäminen tekee taulukosta jo huteron, joissain soluissa havaintojen määrä pienenee. Kaikissa soluissa on sentään viisi havaintoa tai enemmän. Pienten massojen profiilien ja harvinaisten kategorioiden vaikutukset on kuitenkin arvioitava, ne voivat joskus, mutta onneksi harvoin, määrittää sitä liikaa.
5.1 Ikä ja sukupuoli
Ikäjakauma painottuu kaikissa maissa jonkin verran vanhempiin ikäluokkiin. Nuorempien ikäluokkien osuus on (alle 26-vuotiaat ja alle 26-35 - vuotiaat) varsinkin Bulgariassa (BG) ja Unkarissa (HU) pieni.
Ikäluokilla on luonnollinen järjestys, niiden pisteet voidaan yhdistää nuorimmasta vanhimpaan.
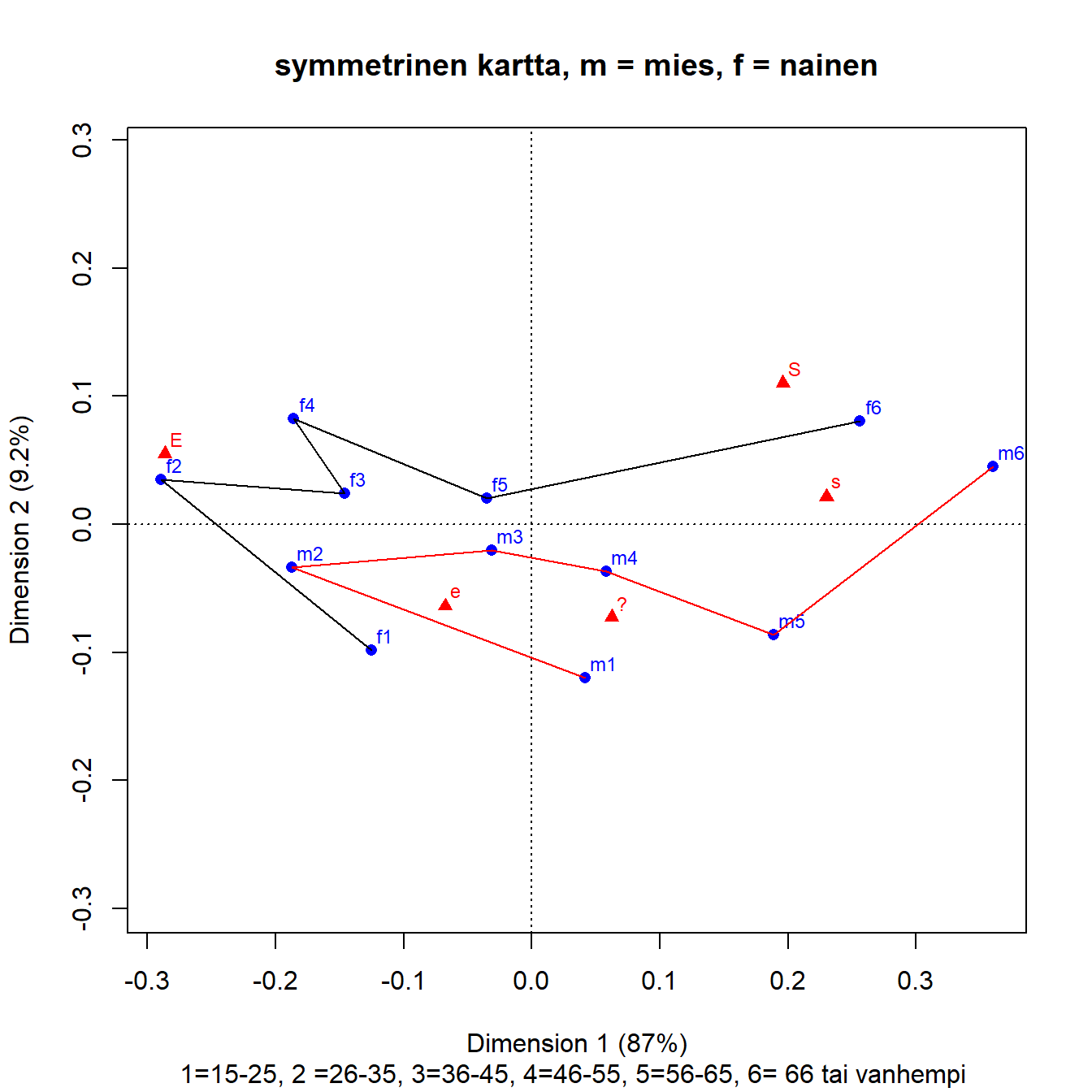
Kuva 5.1: Q1b: ikäluokka ja sukupuoli
Ratkaisu on melko yksiulotteinen, ensimmäinen dimensio kuvaa 87 prosenttia kokonaisinertiasta. Dimensioiden tulkinta on suurin piirtein sama kuin edellisissä kartoissa, mutta S-sarake on kiusallisesti s-sarakkeen vasemmalla puolella. Numeerisista tuloksista näkee (ks. tuloste alla), että sarakkeiden s ja E osuus kokonaisinertiasta (sarake inr) on 768. Niiden kontribuutio x-akselille on yhteensä vielä suurempi (849). Muut sarakkeet taas kontribuoivat y-akselin inertiaan, mutta sen osuus kokonaisinertiasta on vain 9 prosenttia. Kun sarakkeet kuitenkin ovat aika hyvin esitettyjä (qlt), voidaan x- akseli tulkinta hieman karkeammin samaa mieltä - eri mieltä - tasolla samaksi liberaalien ja konservatiivisten asenteiden ulottuvuudeksi. Toinen dimensio kuvaa tiukempaa samanmielisyyttä (S), kontrastina neutraali (?) ja maltillinen erimielisyys (s).
##
## Principal inertias (eigenvalues):
##
## dim value % cum% scree plot
## 1 0.037448 87.0 87.0 **********************
## 2 0.003977 9.2 96.2 **
## 3 0.001041 2.4 98.6 *
## 4 0.000590 1.4 100.0
## -------- -----
## Total: 0.043055 100.0
##
##
## Rows:
## name mass qlt inr k=1 cor ctr k=2 cor ctr
## 1 | f1 | 60 990 36 | -125 614 25 | -98 376 145 |
## 2 | f2 | 83 997 163 | -289 983 185 | 35 14 25 |
## 3 | f3 | 91 984 47 | -146 958 52 | 24 26 13 |
## 4 | f4 | 101 1000 97 | -186 836 93 | 82 164 172 |
## 5 | f5 | 98 879 4 | -35 658 3 | 20 221 10 |
## 6 | f6 | 100 951 176 | 256 866 175 | 80 85 162 |
## 7 | m1 | 57 659 32 | 42 72 3 | -120 587 205 |
## 8 | m2 | 66 977 57 | -187 946 62 | -34 30 19 |
## 9 | m3 | 78 457 5 | -31 318 2 | -20 139 8 |
## 10 | m4 | 89 674 14 | 58 482 8 | -37 192 30 |
## 11 | m5 | 89 988 90 | 189 818 85 | -86 170 166 |
## 12 | m6 | 89 978 277 | 360 963 307 | 45 15 45 |
##
## Columns:
## name mass qlt inr k=1 cor ctr k=2 cor ctr
## 1 | S | 99 915 128 | 196 695 102 | 110 220 304 |
## 2 | s | 238 969 304 | 230 961 336 | 21 8 27 |
## 3 | | 168 777 46 | 62 330 17 | -73 447 223 |
## 4 | e | 261 897 58 | -68 473 32 | -64 424 268 |
## 5 | E | 234 997 464 | -286 962 513 | 55 35 177 |Rivien massat ovat melko samankokoisia, mutta kolmen ryhmän (f2, f6 ja m6) osuus kokonaisinertiasta on 616 ja niiden kontribuutio ensimmäiselle dimensiolle on 567. Vain 36-45-vuotiaiden miesten (m3) piste on huonosti esitetty (qlt = 457). Tulkinta on hankalaa miesten ja naisten nuorimman ryhmän osalta, vaikka efekti kartalla on iso. Molempien osuus kokonaisinertiasta on pieni (inr). Nuoret naiset (f1) on kuvattu kartalla erittäin hyvin. Nuorten miesten (m1) esityksen laatu on heikompi, ja kaikista suurin kontribuutio on vain y-akselille. Kun muut ikäryhmät (paitsi f3) ovat ikäjärjestyksessä vasemmalta oikealle, voi nuorimpien ja vanhimpien ikäryhmien sijainnin tulkita osittain toisen dimension (varma mielipide - epävarma mielipide) avulla.
Selvästi kaikissa ikäluokissa miehet ovat konservatiivisempia kuin naiset. Nuorin ikäluokka on vähemmän varma mielipiteistään kuin vanhin. Yksi mahdollinen selitys kartan tulkinnan ongelmille on se, että maiden väliset erot mielipiteissä ovat paljon suurempia kuin sukupuolten väliset maiden sisällä (ISSP 1994 aineisto, CAiP, s.126).
5.2 Ikä, sukupuoli ja maa
Ikäluokan, sukupuolen ja maan yhteisvaikutusmuuttuja lisää kuvapisteiden määrää. Kuvasta 5.2 saa jotenkin selvää, kun sen suurentaa mutta pisteitä on selvästi liikaa. Joitain muuttujien nimiä voisi lyhentää, kuva-alaa voisi rajata joihinkin osiin mutta osajoukon korrespondenssianalyysi tarjoaa pätevimmän vaihtoehdon.
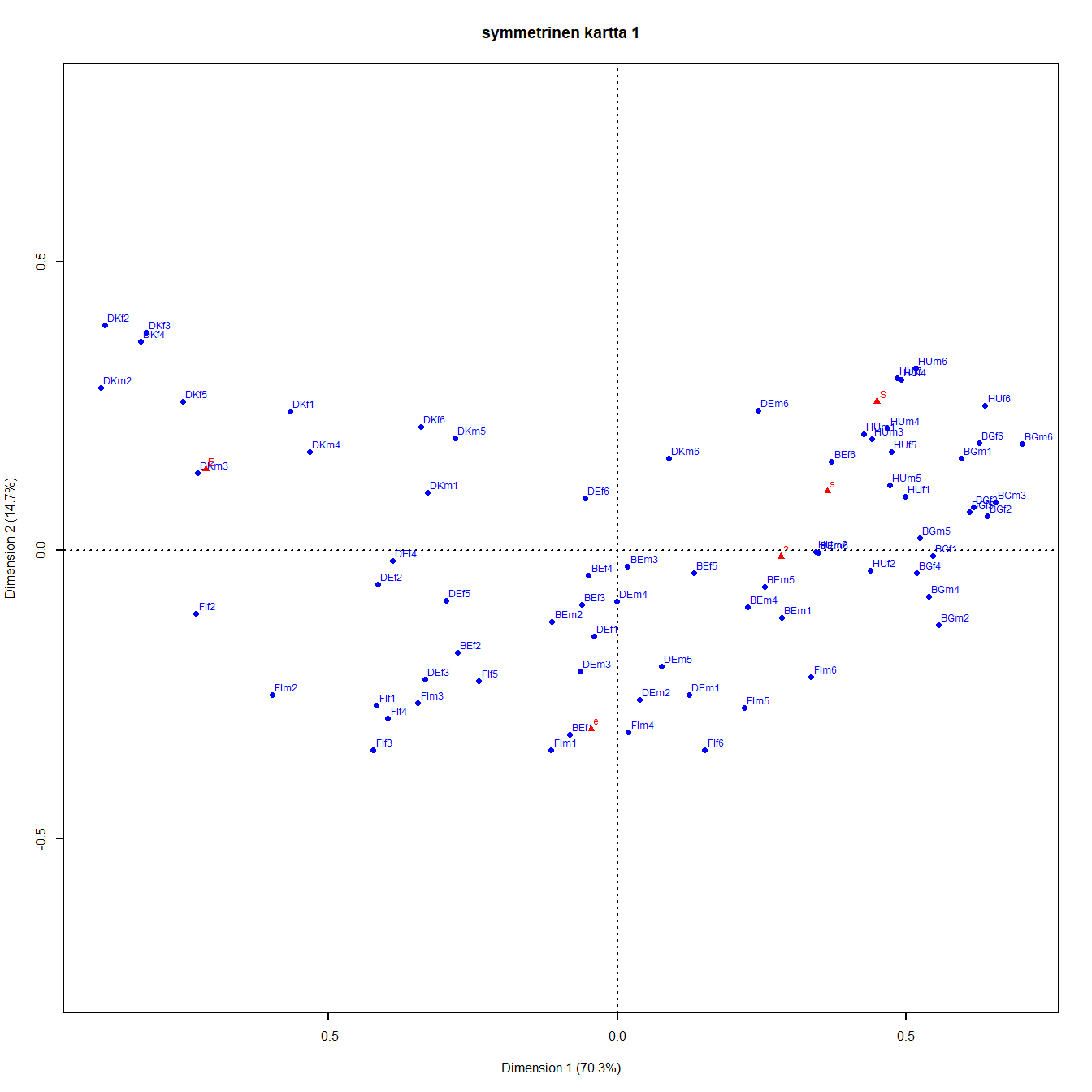
Kuva 5.2: Q1b: ikäluokka ja sukupuoli maittain
Sarakkeiden järjestys vasemmalta oikealle ja ylhäältä alas on sama kuin edellisissä kartoissa. Dimensioiden tulkinta on sama, osuus inertiasta pienenee x-akselilla noin 6 prosenttiyksikköä. Pisteiden järjestys liberaalista konservatiiviseen alkaa Tanskan ja Suomen pisteistä, sitten tulevat Saksan ja Belgian pisteet ja konservatiivisimpia ovat oikeassa laidassa Unkari ja Bulgaria. Toisella akselilla maltillisia ja neutraaleja ovat karkeasti Suomen pisteet ja lähes kaikki Saksan ja Belgian pisteet. Eri maiden osajoukkojen suhteita on hankalampi hahmottaa, erityisesti kartan oikealla laidalla.
Numeeristen tulosten taulukko on pitkä (ks. alle), mutta kartan informaatio pitää varmistaa. Numeeriset tulokset eivät ole pelkkää diagnostiikkaa ja kartan esittämien riippuvuuksien varmistamista. Niistä näkee myös tarkemmin mahdolliset kiinnostavat piirteet datassa. Regressiomallien tulosten raporteissa diagnostiikka on usein liitteenä, mutta eksploratiivisessa data-analyysissä se ohjaa analyysiä eteenpäin.
Tässä voi nähdä myös todennäköisyysteoriaan perustuvan tilastollisen mallintamisen vahvan puolen, aineiston rakenne ja muuttujien yhteydet saadaan parhaassa tapauksessa esitettyä paljon tiiviimmin.
##
## Principal inertias (eigenvalues):
##
## dim value % cum% scree plot
## 1 0.184895 70.3 70.3 ******************
## 2 0.038751 14.7 85.0 ****
## 3 0.024006 9.1 94.1 **
## 4 0.015502 5.9 100.0 *
## -------- -----
## Total: 0.263154 100.0
##
##
## Rows:
## name mass qlt inr k=1 cor ctr k=2 cor ctr
## 1 | BEf1 | 14 678 9 | -83 43 1 | -320 635 38 |
## 2 | BEf2 | 24 914 11 | -278 650 10 | -177 264 20 |
## 3 | BEf3 | 21 320 3 | -62 96 0 | -95 224 5 |
## 4 | BEf4 | 24 164 3 | -50 92 0 | -44 71 1 |
## 5 | BEf5 | 23 332 5 | 133 304 2 | -40 28 1 |
## 6 | BEf6 | 23 832 17 | 371 710 17 | 153 121 14 |
## 7 | BEm1 | 11 429 9 | 284 367 5 | -117 62 4 |
## 8 | BEm2 | 17 372 5 | -113 169 1 | -125 203 7 |
## 9 | BEm3 | 20 108 1 | 17 29 0 | -29 79 0 |
## 10 | BEm4 | 22 966 5 | 225 812 6 | -98 154 5 |
## 11 | BEm5 | 22 728 8 | 255 686 8 | -63 42 2 |
## 12 | BEm6 | 26 788 15 | 348 788 17 | -5 0 0 |
## 13 | BGf1 | 5 531 11 | 547 531 8 | -9 0 0 |
## 14 | BGf2 | 8 860 14 | 640 853 17 | 59 7 1 |
## 15 | BGf3 | 12 815 21 | 617 804 24 | 75 12 2 |
## 16 | BGf4 | 10 932 12 | 519 927 15 | -39 5 0 |
## 17 | BGf5 | 14 880 23 | 609 870 28 | 66 10 2 |
## 18 | BGf6 | 18 921 32 | 627 846 39 | 186 74 16 |
## 19 | BGm1 | 5 940 7 | 596 878 9 | 159 62 3 |
## 20 | BGm2 | 6 830 9 | 557 788 11 | -130 43 3 |
## 21 | BGm3 | 8 709 19 | 655 698 19 | 83 11 1 |
## 22 | BGm4 | 8 771 11 | 540 754 12 | -81 17 1 |
## 23 | BGm5 | 10 979 11 | 524 977 15 | 21 2 0 |
## 24 | BGm6 | 9 692 27 | 701 647 24 | 184 45 8 |
## 25 | DEf1 | 13 425 3 | -41 29 0 | -149 395 7 |
## 26 | DEf2 | 15 938 10 | -415 919 14 | -60 19 1 |
## 27 | DEf3 | 19 846 13 | -333 582 11 | -224 264 24 |
## 28 | DEf4 | 23 985 13 | -390 982 19 | -18 2 0 |
## 29 | DEf5 | 17 839 7 | -297 772 8 | -87 67 3 |
## 30 | DEf6 | 23 116 8 | -56 32 0 | 90 84 5 |
## 31 | DEm1 | 13 912 4 | 124 180 1 | -250 732 20 |
## 32 | DEm2 | 13 766 4 | 38 16 0 | -259 749 22 |
## 33 | DEm3 | 15 737 4 | -64 63 0 | -210 674 17 |
## 34 | DEm4 | 21 137 5 | -1 0 0 | -89 137 4 |
## 35 | DEm5 | 19 603 5 | 76 75 1 | -202 529 20 |
## 36 | DEm6 | 22 849 12 | 244 427 7 | 242 422 34 |
## 37 | DKf1 | 10 991 15 | -567 839 18 | 241 152 15 |
## 38 | DKf2 | 14 991 49 | -888 831 58 | 389 160 53 |
## 39 | DKf3 | 17 963 53 | -816 793 60 | 377 170 61 |
## 40 | DKf4 | 18 977 57 | -826 820 66 | 362 157 61 |
## 41 | DKf5 | 16 998 38 | -753 894 48 | 258 105 27 |
## 42 | DKf6 | 12 808 9 | -340 579 8 | 214 229 14 |
## 43 | DKm1 | 15 981 7 | -329 898 9 | 100 83 4 |
## 44 | DKm2 | 13 989 43 | -895 900 55 | 282 89 26 |
## 45 | DKm3 | 13 982 28 | -728 950 38 | 134 32 6 |
## 46 | DKm4 | 15 941 19 | -534 855 24 | 170 86 11 |
## 47 | DKm5 | 13 643 9 | -281 435 6 | 194 208 13 |
## 48 | DKm6 | 15 355 5 | 89 85 1 | 158 270 9 |
## 49 | FIf1 | 12 980 11 | -417 693 11 | -269 287 21 |
## 50 | FIf2 | 12 927 26 | -730 907 34 | -110 21 4 |
## 51 | FIf3 | 12 984 13 | -423 590 11 | -346 394 36 |
## 52 | FIf4 | 14 991 14 | -398 644 12 | -292 347 32 |
## 53 | FIf5 | 17 952 8 | -240 502 5 | -227 450 23 |
## 54 | FIf6 | 11 835 7 | 151 134 1 | -347 701 35 |
## 55 | FIm1 | 7 787 5 | -115 78 1 | -347 710 22 |
## 56 | FIm2 | 9 977 14 | -598 832 17 | -250 146 14 |
## 57 | FIm3 | 9 998 6 | -345 629 6 | -265 369 16 |
## 58 | FIm4 | 13 837 6 | 19 3 0 | -316 834 33 |
## 59 | FIm5 | 12 734 7 | 220 289 3 | -273 446 23 |
## 60 | FIm6 | 9 911 6 | 336 637 6 | -220 274 12 |
## 61 | HUf1 | 7 723 9 | 499 698 9 | 93 25 1 |
## 62 | HUf2 | 11 689 11 | 438 685 11 | -35 4 0 |
## 63 | HUf3 | 12 808 18 | 484 586 15 | 298 222 27 |
## 64 | HUf4 | 11 768 18 | 491 564 15 | 296 204 25 |
## 65 | HUf5 | 12 850 13 | 474 753 14 | 170 97 9 |
## 66 | HUf6 | 13 671 34 | 637 581 28 | 251 90 21 |
## 67 | HUm1 | 6 935 5 | 426 766 6 | 201 170 6 |
## 68 | HUm2 | 9 381 11 | 344 381 6 | -2 0 0 |
## 69 | HUm3 | 13 957 12 | 441 803 13 | 193 154 12 |
## 70 | HUm4 | 10 999 10 | 468 830 12 | 211 169 11 |
## 71 | HUm5 | 13 942 12 | 472 891 15 | 113 51 4 |
## 72 | HUm6 | 8 726 15 | 517 529 11 | 315 197 20 |
##
## Columns:
## name mass qlt inr k=1 cor ctr k=2 cor ctr
## 1 | S | 99 653 155 | 450 492 109 | 258 162 171 |
## 2 | s | 238 741 174 | 364 687 170 | 102 54 63 |
## 3 | | 168 535 96 | 284 534 73 | -11 1 1 |
## 4 | e | 261 941 103 | -45 20 3 | -310 921 646 |
## 5 | E | 234 1000 471 | -714 962 645 | 141 37 119 |Tuloksista nähdään, että sarakkeet on kohtalaisen hyvin esitetty, heikoimmin neutraali vaihtoehto (qlt = 535). Kun sen suhteellinen kontribuutio (cor) on vain 1 toisella dimensiolla jää loppuosa x-akselille. Maltillisuuden dimensiota määrittää e-sarake (ctr = 646), ja vain sitä. Ensimmäistä dimensiota määrittää vahvimmin E-sarake (ctr = 645) liberaaliin ja samaa mieltä olevien sarakkeet (s, S) konservatiiviseen suuntaan.
Kun aineistossa on 72 riviä, on inertian suhteellisen kontribuution keskiarvo noin 14. Tämän ylittäviä kontribuutiota on Bulgarian naisilla (BGf2, BGf3, BGf5 ja BGf6), kaikilla konservatiiviseen suuntaan. Sama pätee Unkarin naisille, muuten naisten ikäluokat kontribuoivat yleensä liberaaliin suuntaan. Suomen pisteiden absoluuttiset kontribuutiot ovat lähes pelkästään toiselle dimensiolle maltilliseen suuntaan. Tanska taas kontribuoi vahvasti jyrkempien mielipiteiden suuntaan.
5.3 Stabiilisuus
Tarkastelen tässä vain ratkaisustabiiliutta (solution stability). Siinä data on annettu, ja ratkaisun numeerisista tuloksista nähdään miten pisteet määrittävät akselit. Ratkaisu on stabiili niiden pisteiden suhteen, jotka eivät vaikuta siihen.
Ulkoinen stabiilius on laajempi käsite, siinä huomioidaan esimerkiksi datan suhde johonkin perusjoukkoon (CAiP, s. 225).
Korrespondenssianalyysiä ja erityisesti khii2- etäisyysmittaa on arvosteltu siitä, että se on liian herkkä harvinaisille luokittelumuuttujan arvoille. Yhteenvetoartikkelissaan M. Greenacre (2006) tarttuu ”vaikuttavien poikkeavien havaintojen myyttiin”, ja pitää sitä lähes aina perusteettomana.
Harvinaiset kategoriat ovat usein kartalla kaukana origosta, mutta jokaisella pisteellä on massa ja näillä poikkeavilla havainnoilla (outlier) se on pieni. Niinpä niiden vaikutuskin on vaatimaton.
Harvinaisten kategorioiden vaikutus voi olla suuri, joten numeerisista tuloksista on tarkistettava, onko hyvin pienen massan pisteillä suuri kontribuutio ratkaisuun. Käytännössä näin voi käydä esimerkiksi silloin, kun jonkun harvinaisen luokittelumuuttujan arvon havainnot ovat keskittyneet muutamaan profiiliin, joissa niiden osuus on suuri (CAiP, s 298). Luvussa 7 nähdään, miten melko vähäinen määrä puuttuvia vastauksia kasaantuu samaan vastaajien osajoukkoon ja mitä seurauksia sillä on.
Stabiiliutta voi helposti kokeilla määrittelemällä joitain pisteitä täydentäviksi pisteiksi.
En löytänyt kartan 5.2 numeerisista tuloksista pienen massan pisteitä, joilla on merkittävä kontribuutio akseleihin.