Luku 6 Osajoukon korrespondenssianalyysi
Graafisessa data-analyysissä kuvien on oltava selkeitä, mutta korrespondenssianalyysin kartat ovat usein liian täynnä pisteitä. Ongelmaa voi lieventää jättämällä pois ratkaisuun vain vähän vaikuttavia pisteitä, keksimällä mahdollisimman lyhyitä symboleja muuttujille tai rajaamalla kuvaa. Ongelma on kuitenkin syvempi, usein kartta kertoo aika yllätyksettömän ja ilmeisen tarinan. Kiinnostavammat yhteydet pysyvät piilossa ylemmissä dimensioissa. MCA-kartan perusongelma on se, että siinä yritetään esittää monia erityyppisiä yhteyksiä simultaanisesti ja nämä yhteydet eivät ole “isolated to particular dimensions” (Greenacre ja Pardo artikkelikokoelmassa (M. Greenacre ja Blasius 2006), s. 198).
Osajoukon korrespondenssianalyysi (subset CA, subset MCA) on yksi vastaus tähän pulmaan. Teoreettiset perusteet on esitetty Greenacren ja Pardon artikkelissa (M. Greenacre ja Pardo 2006). Artikkelin laajennetussa versiossa (emt.) esimerkkiaineistona on ISSP:n 1994 data. Selkeä oppikirjaesitys on CAiP (ss. 161-).
Eräs sovelluskohde yhteiskuntatieteellisissä kyselyaineistoissa on puuttuvien vastausten analyysi, johon palataan seuraavassa luvussa.
Osajoukon korrespondenssianlyysin idea on säilyttää koko aineiston massat ja khii2-etäisyyksien painot mutta analysoida vain osaa aineistosta. Koko aineiston sentroidi säilyy kartan keskipisteenä. Osajoukkojen inertioiden summa on koko aineiston inertia.
Osajoukon voi valita havaintojen tai muuttujien suhteen. Täydentäviä pisteitä voi helposti lisätä kartalle, jos ne eivät kuulu siihen joukkoon, josta osajoukko on valittu. Osajoukon profiilit muuttuvat, niiden summa ei enää ole yksi ja barysentristä periaatetta ei voi suoraan käyttää täydentävän pisteen koordinaattien laskemiseen. Tässä esimerkissä emme voi suoraan ca-paketin avulla sijoittaa esimerkiksi maapisteitä kartoille.
Kartan 5.2 avulla aineiston voi jakaa kahteen ryhmään. Suomi, Tanska ja Saksa ovat pääakselin oikealla puolella. Bulgaria ja Unkari ja Belgian kanssa ovat toinen ryhmä.
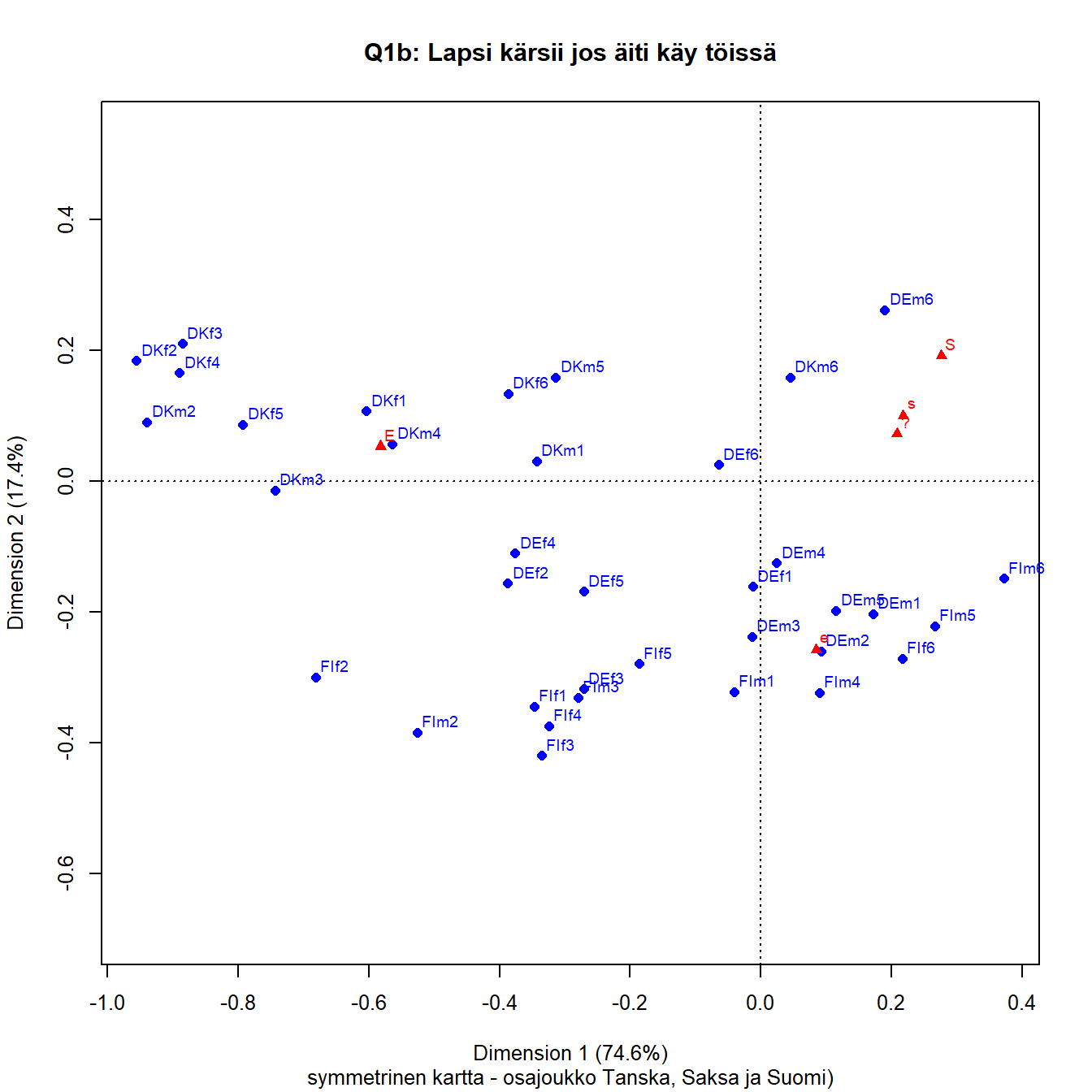
Kuva 6.1: Ikä, sukupuoli ja maa:Tanska-Saksa-Suomi
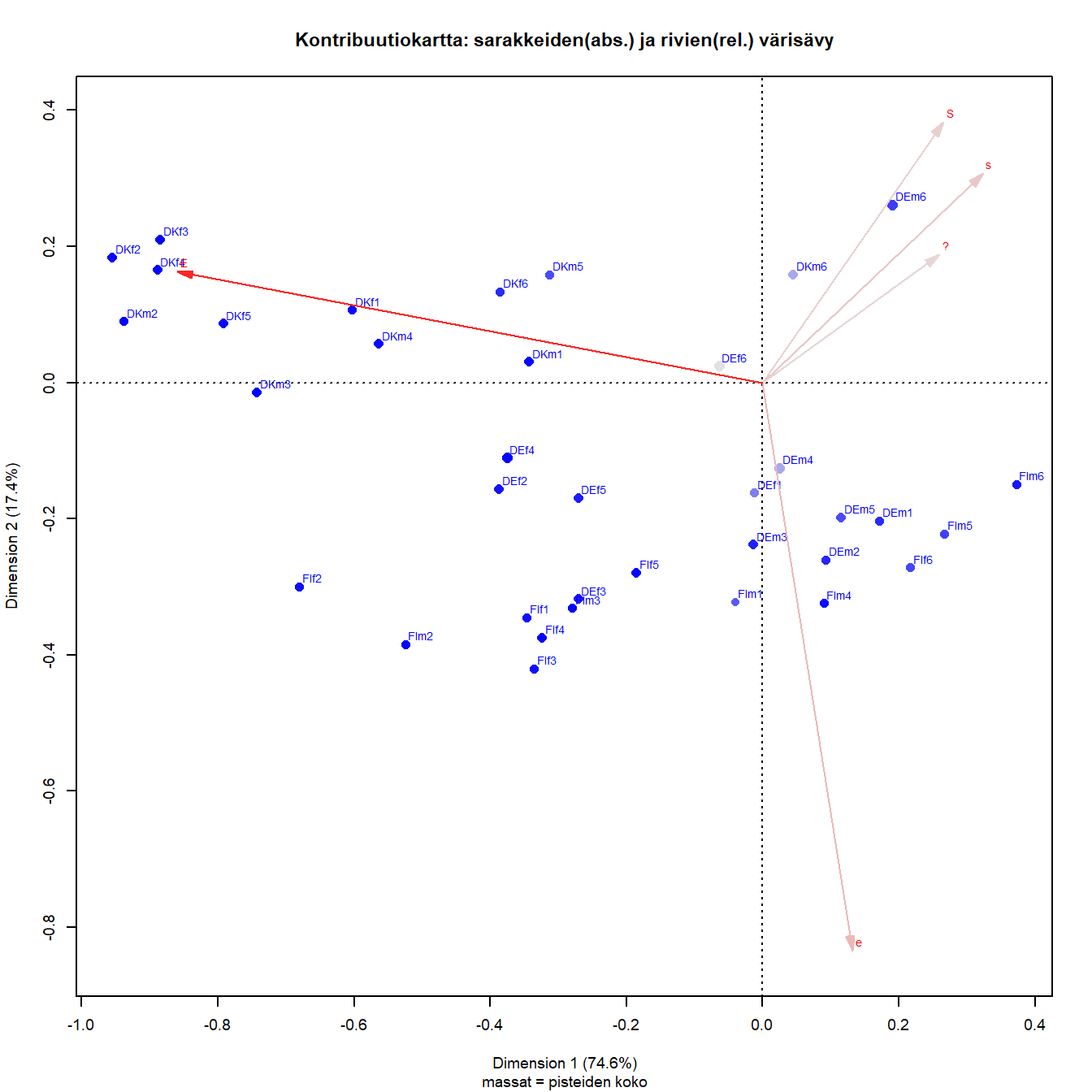
Kuva 6.2: Ikä, sukupuoli ja maa:Tanska-Saksa-Suomi
Karttoja 6.1 ja 6.2 joutuu katsomaan aika tarkkaan ennen kuin uskoo, että akseleiden skaalaus on akateeminen pulma vailla käytännön merkitystä (kts. luku 3.4). Dataa analysoidaan graafisesti, ja kuvat näyttävät erilaisilta. Pääakselien inertioiden neliöjuuret eivät poikkea toisistaan huomattavasti (0.327 ja 0.158), joten sarakkeiden etäisyyksiä voisi tulkita myös kontribuutiokuvista.
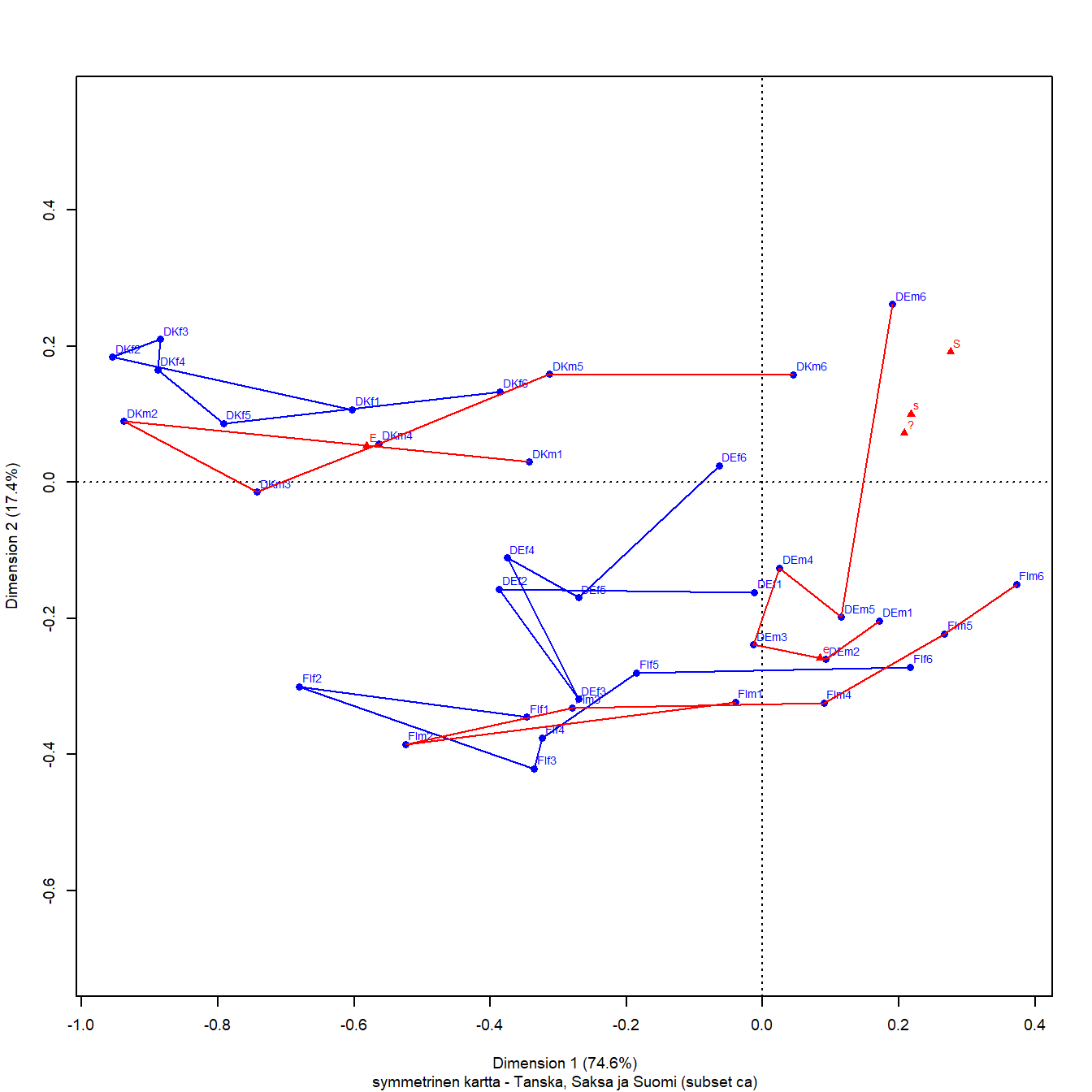
Kuva 6.3: Ikä, sukupuoli ja maa:Tanska-Saksa-Suomi
##
## Principal inertias (eigenvalues):
##
## dim value % cum% scree plot
## 1 0.107090 74.6 74.6 *******************
## 2 0.024985 17.4 92.0 ****
## 3 0.006594 4.6 96.6 *
## 4 0.004882 3.4 100.0 *
## -------- -----
## Total: 0.143551 100.0
##
##
## Rows:
## name mass qlt inr k=1 cor ctr k=2 cor ctr
## 1 | DEf1 | 13 467 5 | -12 3 0 | -162 464 13 |
## 2 | DEf2 | 15 930 19 | -387 799 21 | -157 131 14 |
## 3 | DEf3 | 19 919 25 | -271 385 13 | -318 533 76 |
## 4 | DEf4 | 23 993 25 | -376 913 30 | -111 80 11 |
## 5 | DEf5 | 17 893 13 | -271 641 11 | -169 252 19 |
## 6 | DEf6 | 23 48 15 | -64 42 1 | 24 6 1 |
## 7 | DEm1 | 13 827 8 | 172 345 3 | -203 482 21 |
## 8 | DEm2 | 13 855 8 | 93 96 1 | -260 759 34 |
## 9 | DEm3 | 15 874 7 | -13 3 0 | -238 871 34 |
## 10 | DEm4 | 21 285 8 | 25 11 0 | -126 274 13 |
## 11 | DEm5 | 19 684 10 | 116 174 2 | -198 510 30 |
## 12 | DEm6 | 22 750 22 | 190 260 8 | 261 490 61 |
## 13 | DKf1 | 10 979 27 | -603 949 35 | 107 30 5 |
## 14 | DKf2 | 14 996 89 | -955 960 115 | 184 36 18 |
## 15 | DKf3 | 17 985 98 | -885 933 122 | 210 53 29 |
## 16 | DKf4 | 18 983 104 | -889 950 132 | 165 33 20 |
## 17 | DKf5 | 16 1000 69 | -792 988 92 | 86 12 5 |
## 18 | DKf6 | 12 834 17 | -386 745 17 | 133 89 9 |
## 19 | DKm1 | 15 978 13 | -342 971 17 | 30 7 1 |
## 20 | DKm2 | 13 997 79 | -938 988 104 | 90 9 4 |
## 21 | DKm3 | 13 989 52 | -743 989 69 | -14 0 0 |
## 22 | DKm4 | 15 962 36 | -563 952 45 | 57 10 2 |
## 23 | DKm5 | 13 682 16 | -314 543 12 | 159 139 13 |
## 24 | DKm6 | 15 291 9 | 45 22 0 | 158 269 15 |
## 25 | FIf1 | 12 951 20 | -346 478 13 | -345 474 55 |
## 26 | FIf2 | 12 941 48 | -680 788 50 | -300 153 42 |
## 27 | FIf3 | 12 952 24 | -335 370 12 | -420 582 82 |
## 28 | FIf4 | 14 999 25 | -323 426 14 | -375 573 82 |
## 29 | FIf5 | 17 982 14 | -185 299 6 | -280 683 55 |
## 30 | FIf6 | 11 704 13 | 217 274 5 | -271 430 33 |
## 31 | FIm1 | 7 624 8 | -40 10 0 | -323 614 30 |
## 32 | FIm2 | 9 984 26 | -525 640 22 | -385 344 52 |
## 33 | FIm3 | 9 990 12 | -279 412 6 | -331 578 38 |
## 34 | FIm4 | 13 944 11 | 90 67 1 | -324 877 54 |
## 35 | FIm5 | 12 722 14 | 267 426 8 | -222 295 23 |
## 36 | FIm6 | 9 911 11 | 373 785 12 | -150 126 8 |
##
## Columns:
## name mass qlt inr k=1 cor ctr k=2 cor ctr
## 1 | S | 99 731 107 | 276 493 71 | 192 238 147 |
## 2 | s | 238 832 114 | 218 688 105 | 100 144 94 |
## 3 | | 168 647 88 | 208 576 68 | 73 70 35 |
## 4 | e | 261 992 135 | 85 96 17 | -258 896 697 |
## 5 | E | 234 1000 556 | -582 992 739 | 53 8 27 |Tulkintaa
Kolmen maan osajoukon ratkaisussa 2. dimensiolla (maltillinen liberaali - tiukka konservatiivi) on inertiasta 17 prosenttia, edellä ollut paljon yksiulotteisempia ratkaisuja. Huono kvaliteetti (qlt) on ryhmillä DEf1 (467) ja DEf6 (48), DEm4 (285). Tanskan havainnoista vanhimmat miehet (DKm6,291) ovat kaikkein huonoimmin esitettyjä ratkaisussa, ja hieman nuoremmatkin (DKm5, 682). Suomen aineistossa vain nuoret miehet (FIm1, 624) on esitetty kartalla huonosti. Kaksi dimensiot selittävät osajoukon kokonaishajonnasta 92 prosenttia, mutta muutaman ryhmän hajonta on muissa dimensioissa. Saksan naisten iäkkäin ikäluokka (DEf6) ja keski-ikäisen miehet (DEm4) vain näyttävät olevan lähekkäin origon tuntumassa, samoin muutama muu huonosti tasoon sijoitettu piste. Huonosti kuvatuista pisteistä kuva ei oikeastaan mitään muuta.
Sarakkeet on esitetty kohtalaisen hyvin, ja symmetrisessä kartassa tärkeimmälle dimensioille projisoidut sarakepisteet ovat odotetussa järjestyksessä.
Kontribuutiokartasta nähdään, että tärkein kontrasti on tiukan erimielisyyden (E) ja kaikkien muiden vastausvaihtoehtojen välillä. Epävarmojen tai maltillisten (e) kontrasti hallitsee toista dimensiota, erityisesti S- ja s- kategorioiden kanssa. Samalla kuvasta näkee (ja numeerisista tuloksista voi vahvistaa), että S-piste on on lähempänä (kulma on pienempi) pystyakselia. Kontribuutio on suurempi (147 vs. 71 x-akselille). Toisaalta x-akseli selittää selvästi suurimman osan kaikkien muiden sarakepisteiden inertiasta, ja y-akseli taas lähes täysin e-pisteen inertian.
Kartasta 6.3 nähdään, että naisten ikäluokat ovat kaikissa maissa liberaalimpia kuin vastaavat miesten ikäluokat. Nuorin ikäluokka on konservatiivisemmalla puolella ja samalla toisella dimensiolla maltillisemmalla puolella. Vanhemmat ikäluokat ovat konservatiivisempia.
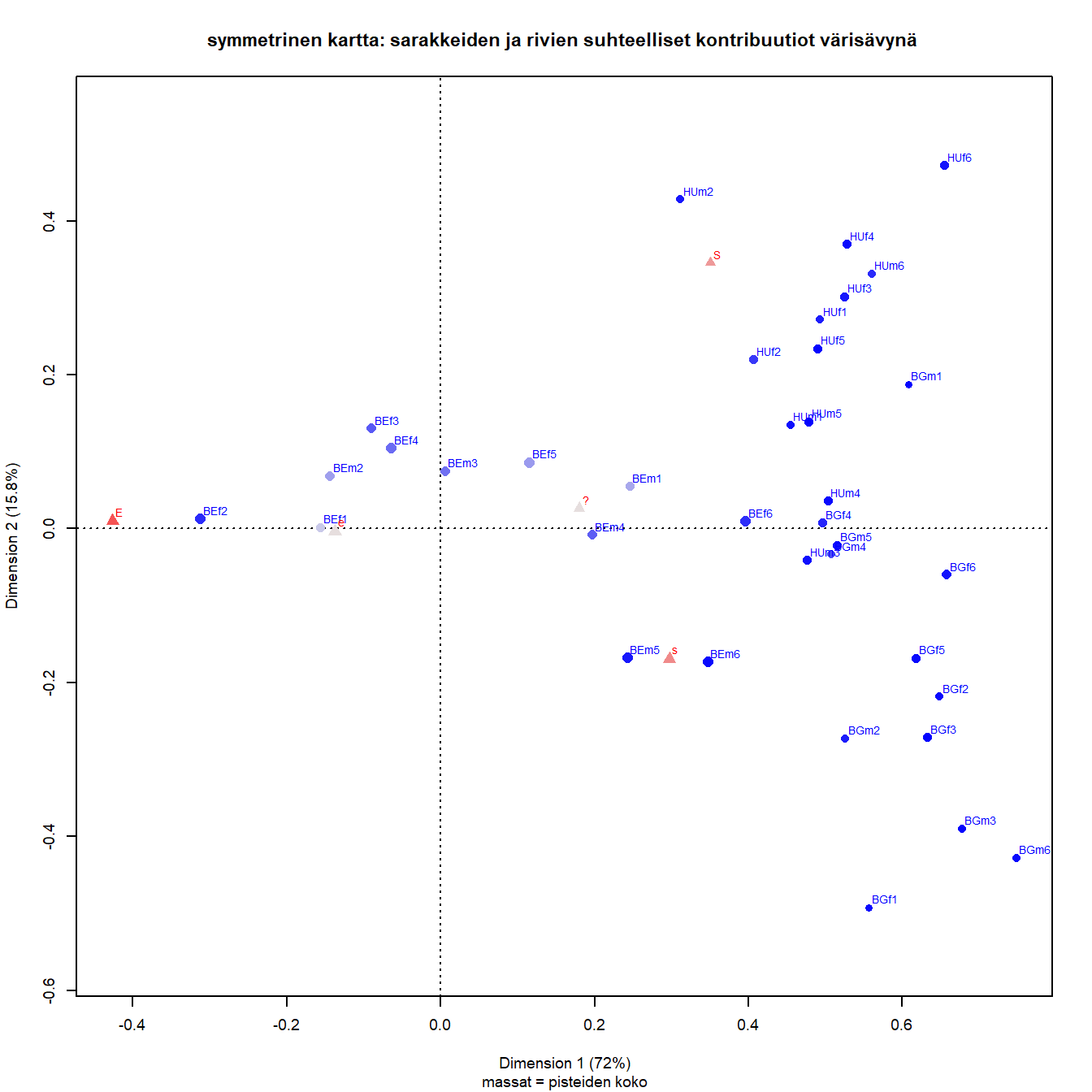
Kuva 6.4: Ikä, sukupuoli ja maa: Belgia-Bulgaria - Unkari
Belgian, Unkarin ja Bulgarian kartalla ensimmäisen dimension tulkinta pysyy samana, mutta nyt molemmat erimieliset (E, e) vastauskategoriat ovat selvästi vasemmalla liberaalilla puolella. Ne ovat lähes x-akselin päällä, kun ensimmäisen osajoukon kartalla e-sarake oli oikealla ja alhaalla kontrastina S- ja s- vastauksille ja myös neutraalille vaihtoehdolle. Kartan toinen dimensio erottelee nyt tiukasti ja lievemmin samaa mieltä olevat, neutraali vaihtoehto jää väliin.
Belgian nuoremmat ikäluokat ovat liberaalilla puolella, ja kiinnostavasti kaksi vanhinta miesten ryhmää on pystysuunnassa kaikkein maltillisimpia. Bulgarian ja Unkarin pisteen ovat tiukasti konservatiivisella puolella. Vaihtelua on maltillisemman ja jyrkemmän konservatiivisuuden välillä pystysuuntaan. Toisen dimension kontrasti on myös hieman yllättäen Bulgarian nuorimpien naisten (BGf1) Unkarin vanhimpien naisten (HUf6) välillä.
Kuvan 6.3 tapaan ei Bulgarian ja Unkarin ikäluokkia kannata yhdistää. Järjestys toki löytyy, mutta ei ollenkaan niin selkeä. Saksan naisten ikäluokkakuva alkaa erkaantua hieman Suomen ja Tanskan hyvin samanlaisista kuvioista. Saksan miehillä on jo eroja paljon toisen dimension suuntaan, Unkarin ja Bulgarian osajoukkojen erot ovat lähes pelkästään pystysuoria.
Suhteellinen kontribuutio eli pisteen laatu (numeerisissa tuloksissa “cor”) on esitetty värisävynä. Sarakkeista e ja “?” on esitetty huonosti, riveistä Belgian nuorimmat miehet ja naiset.
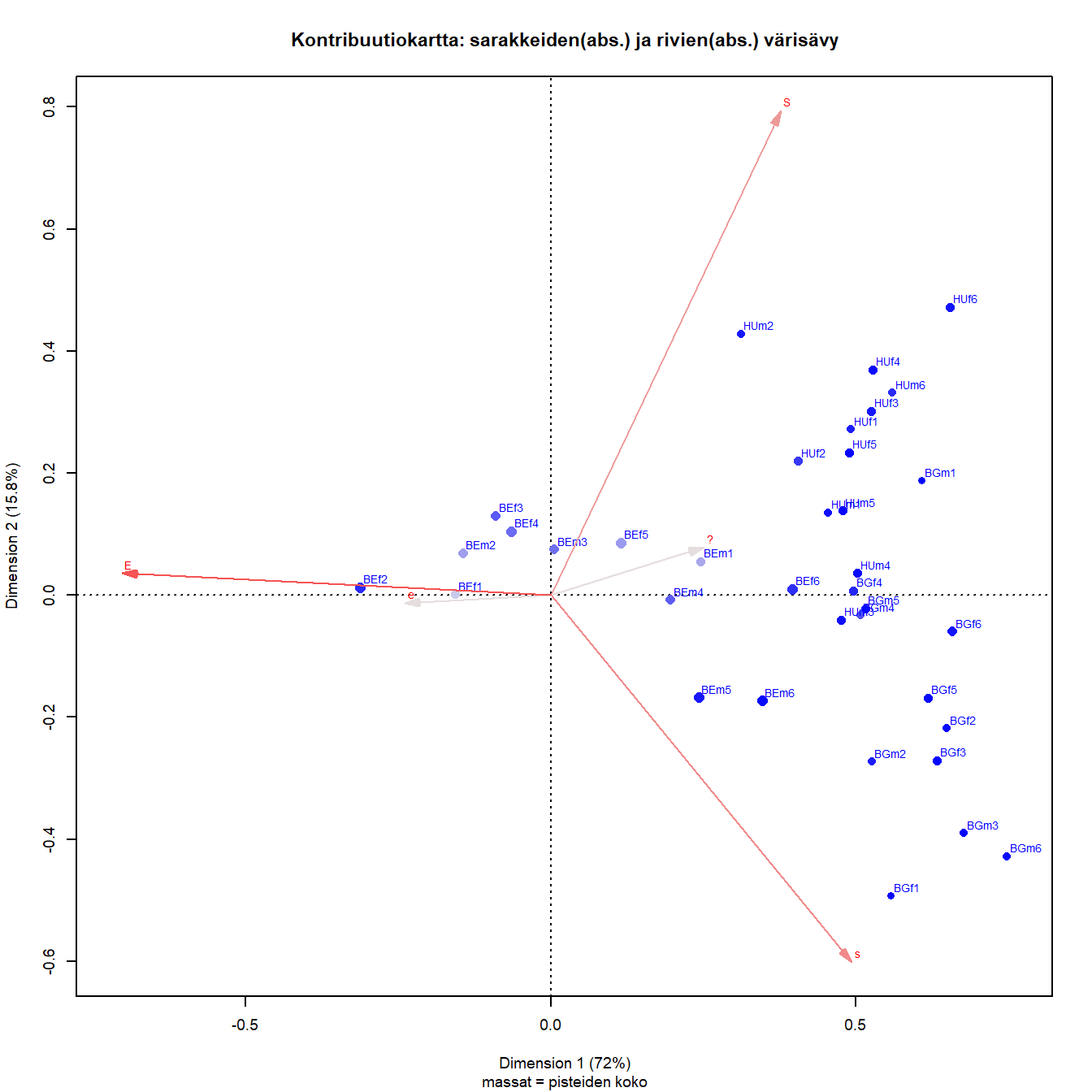
Kuva 6.5: Ikä, sukupuoli ja maa: Belgia-Bulgaria - Unkari 2
Kontribuutiokartta 6.5 eroaa kartasta 6.2 kolmen akselin (E, S ja s) erilaisella vaikutuksella ratkaisuun. Konservatiiviset sarakepisteet ovat vaikuttavampia kuin E, maltillinen liberaali (s) ja neutraali vaihtoehto vaikuttavat vähemmän.
Listataan vielä toisen osajoukon ratkaisun numeeriset tulokset.
##
## Principal inertias (eigenvalues):
##
## dim value % cum% scree plot
## 1 0.086111 72.0 72.0 ******************
## 2 0.018841 15.8 87.8 ****
## 3 0.011172 9.3 97.1 **
## 4 0.003477 2.9 100.0 *
## -------- -----
## Total: 0.119602 100.0
##
##
## Rows:
## name mass qlt inr k=1 cor ctr k=2 cor ctr
## 1 | BEf1 | 14 152 19 | -156 152 4 | 2 0 0 |
## 2 | BEf2 | 24 826 24 | -313 824 28 | 13 1 0 |
## 3 | BEf3 | 21 623 7 | -90 201 2 | 130 422 19 |
## 4 | BEf4 | 24 556 6 | -65 155 1 | 105 401 14 |
## 5 | BEf5 | 23 355 11 | 115 227 3 | 86 128 9 |
## 6 | BEf6 | 23 810 37 | 396 810 41 | 10 0 0 |
## 7 | BEm1 | 11 288 21 | 246 274 8 | 55 14 2 |
## 8 | BEm2 | 17 333 11 | -144 271 4 | 68 61 4 |
## 9 | BEm3 | 20 531 2 | 6 4 0 | 75 528 6 |
## 10 | BEm4 | 22 620 11 | 197 618 10 | -8 1 0 |
## 11 | BEm5 | 22 917 18 | 243 620 15 | -168 297 33 |
## 12 | BEm6 | 26 977 33 | 347 782 36 | -173 195 41 |
## 13 | BGf1 | 5 979 23 | 557 549 18 | -492 430 63 |
## 14 | BGf2 | 8 974 32 | 649 875 38 | -219 99 20 |
## 15 | BGf3 | 12 1000 46 | 633 844 54 | -271 155 45 |
## 16 | BGf4 | 10 847 25 | 496 847 30 | 7 0 0 |
## 17 | BGf5 | 14 961 50 | 618 894 62 | -168 66 21 |
## 18 | BGf6 | 18 939 71 | 658 931 92 | -60 8 4 |
## 19 | BGm1 | 5 999 15 | 608 912 19 | 188 87 9 |
## 20 | BGm2 | 6 892 21 | 526 703 20 | -273 189 25 |
## 21 | BGm3 | 8 994 41 | 677 746 43 | -390 247 64 |
## 22 | BGm4 | 8 669 25 | 508 666 23 | -34 3 0 |
## 23 | BGm5 | 10 949 24 | 516 947 32 | -22 2 0 |
## 24 | BGm6 | 9 978 58 | 748 737 60 | -428 241 89 |
## 25 | HUf1 | 7 888 20 | 493 681 19 | 271 207 26 |
## 26 | HUf2 | 11 762 25 | 406 589 20 | 220 173 27 |
## 27 | HUf3 | 12 916 39 | 525 688 37 | 301 227 56 |
## 28 | HUf4 | 11 970 40 | 528 651 36 | 370 319 81 |
## 29 | HUf5 | 12 985 29 | 490 802 32 | 234 183 34 |
## 30 | HUf6 | 13 933 75 | 655 614 64 | 472 319 151 |
## 31 | HUm1 | 6 948 12 | 455 871 14 | 135 77 6 |
## 32 | HUm2 | 9 902 24 | 312 313 10 | 428 589 90 |
## 33 | HUm3 | 13 945 26 | 477 938 33 | -41 7 1 |
## 34 | HUm4 | 10 965 22 | 503 960 29 | 36 5 1 |
## 35 | HUm5 | 13 993 26 | 478 916 33 | 139 77 13 |
## 36 | HUm6 | 8 839 33 | 560 622 29 | 331 217 46 |
##
## Columns:
## name mass qlt inr k=1 cor ctr k=2 cor ctr
## 1 | S | 99 944 214 | 351 479 142 | 346 465 630 |
## 2 | s | 238 942 247 | 297 711 244 | -169 231 362 |
## 3 | | 168 435 107 | 180 426 63 | 26 9 6 |
## 4 | e | 261 640 65 | -138 639 57 | -4 0 0 |
## 5 | E | 234 966 368 | -426 965 494 | 10 1 1 |Kahden osajoukon inertioiden summa on sama kuin koko aineiston (0.144 + 0.12 = 0.263). Selitysasteet nousevat hieman, ja aineiston riippuvuuden rakenteesta saadaan esiin selviä eroja. Osajoukkojen analyysi täydentää ja tarkentaa yleiskuvaa (ks. Kuva 5.2).
Belgian pisteistä osalla on huono kvaliteetti (BEf1, BEf5, BEm1, BEm2). Bulgaria ja Unkari hyvin esitetty. Belgia on pulmallinen tapaus, ehkä taas omissa dimensioissaan. Belgian poikkeavuus (annetulla aluejaolla) on kiinnostava havainto, korrespondenssianalyysin tavoite ei ole pelkästään kohtuullisen luotettava yleiskuva taulukon riippuvuuksista. Poikkeavat havainnot eivät ole ongelma, vaan datan ominaisuus.