Luku 7 Monimuuttujakorrespondenssianalyysi (MCA)

Usean muuttujan samanaikainen analyysi voidaan korrespondenssianalyysissä jakaa kahteen erilaiseen tutkimusasetelmaan. Ensimmäisessä tutkitaan kahden erilaisen muuttujaryhmän välisiä suhteita, toisessa yhden homogeenisen muuttujaryhmän sisäisiä suhteita.

Esimerkkiaineistossa haastateltavien vastaukset substanssikysymyksiin ovat oma ryhmänsä ja taustamuuttujat toinen ryhmä. Kahden muuttujaryhmän välisiä suhteita voidaan tutkia rakentamalla yhdistetty matriisi useasta kahden muuttujan ristiintaulukoinnista. Tämä pinottujen ja yhdistettyjen (stacked and concatenated) taulukoiden menetelmä (CAiP s. 129) ei kerro muuttujaryhmien sisäisistä yhteyksistä, joita edellä analysoitiin vuorovaikutusmuuttujien avulla.

Toinen asetelma on keskenään homogeenisten muuttujien välisten suhteiden analyysi. Monimuuttujakorrespondenssianalyysi (multiple correspondence analysis, MCA) soveltuu hyvin kyselytutkimusten vastausten analyysiin. MCA - kartoilla voidaan esittää myös havainnot, mutta usein on järkevämpää käyttää kartalla taustamuuttujien keskiarvopisteitä. Keskiarvopisteisiin voi simuloimalla lisätä luottamusellipsit (CAiP, s. 299).

Esitän molemmista analyyseistä yhden esimerkin. MCA-esimerkissä otan käyttöön kaikki aineiston havainnot ja useita vastausmuuttujia, puuttuvat tiedot ovat mukana yhtenä luokittelumuuttujan arvona.

Yksinkertaisen korrespondenssianalyysin yleistys usean muuttujan samanaikaiseen analyysiin ei ole aivan yksikertainen asia. Geometrinen tulkinta ei ole läheskään niin selkeä kuin yksinkertaisessa korrespondenssianalyysissä. Silti MCA toimii käytännössä usein hyvin juuri kyselytutkimusten analyysissä. MCA-kartat esittävät luokittelumuuttujien arvot kartalla optimaalisesti. Jokainen rivipiste (havainto) sijoittuu kartalle valitsemiensa vastausvaihtoehtojen keskiarvopisteeseen. MCA-kartalla nämä luokittelumuuttujien arvoja vastaavat sarakepisteet maksimoivat rivipisteiden hajonnan kartalla (Greenacre ja Hastie 1987 , s. 444-445).

7.1 Pinotut ja yhdistetyt taulukot

Pinottujen taulukoiden idea on esitetty kuvassa 7.1. Taulukossa kaksi “selitettävää” muuttujaa on ristiintaulukoitu kolmen taustamuuttujan kanssa.

Jos reunajakaumat ovat samat eli puuttuvia tietoja ei ole, taulukon kokonaisinertia on osataulukoiden inertioiden keskiarvo. Taulukon analyysi on yhden kysymyksen ja yhden taustamuuttujan parittaisten suhteiden analyysiä, yksi pari kerrallaan.

Pierre Bourdieun tunnettu tutkimus La Distiction (1979) sovelsi tätä menetelmää. Ranskan väestö luokitellaan ammattiryhmiin ja taulukoidaan useiden elämäntapaa kuvaavien muuttujien kanssa. Taulukot yhdistetään pinoamalla ne päällekkäin (M. Greenacre ja Blasius (2006) , s.21).

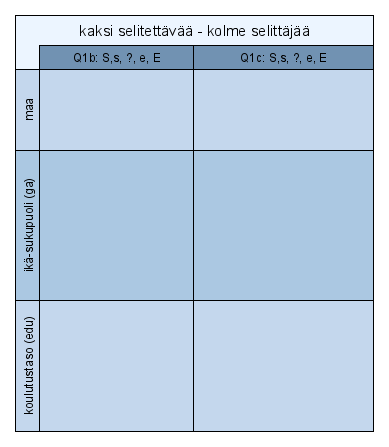
Kuva 7.1: Pinotut ja yhdistetyt taulut - periaate

Seuraavassa esimerkissä “selitettäviä” luokittelumuuttujia on vain yksi. Tällainen pinotun taulun analyysi on eräänlainen kaikkien siihen kuuluvien taulukoiden “keskiarvokartta” (CAiP, s 136). Kysymyksen Q1b vastausten ristiintaulukointi ikäluokan ja sukupuolen kanssa liitetään maarivien taulukkoon.

Pisteiden määrä kartoilla kasvaa, ja muuttujanimiä joudutaan tiivistämään. Toinen tekninen detalji on kartan kääntäminen. Kuvat kääntyvät herkästi akselien ympäri, vertailun helpottamiseksi koordinaattien etumerkkejä joutuu joskus muuttamaan (kts. Liite 3: R-koodi).

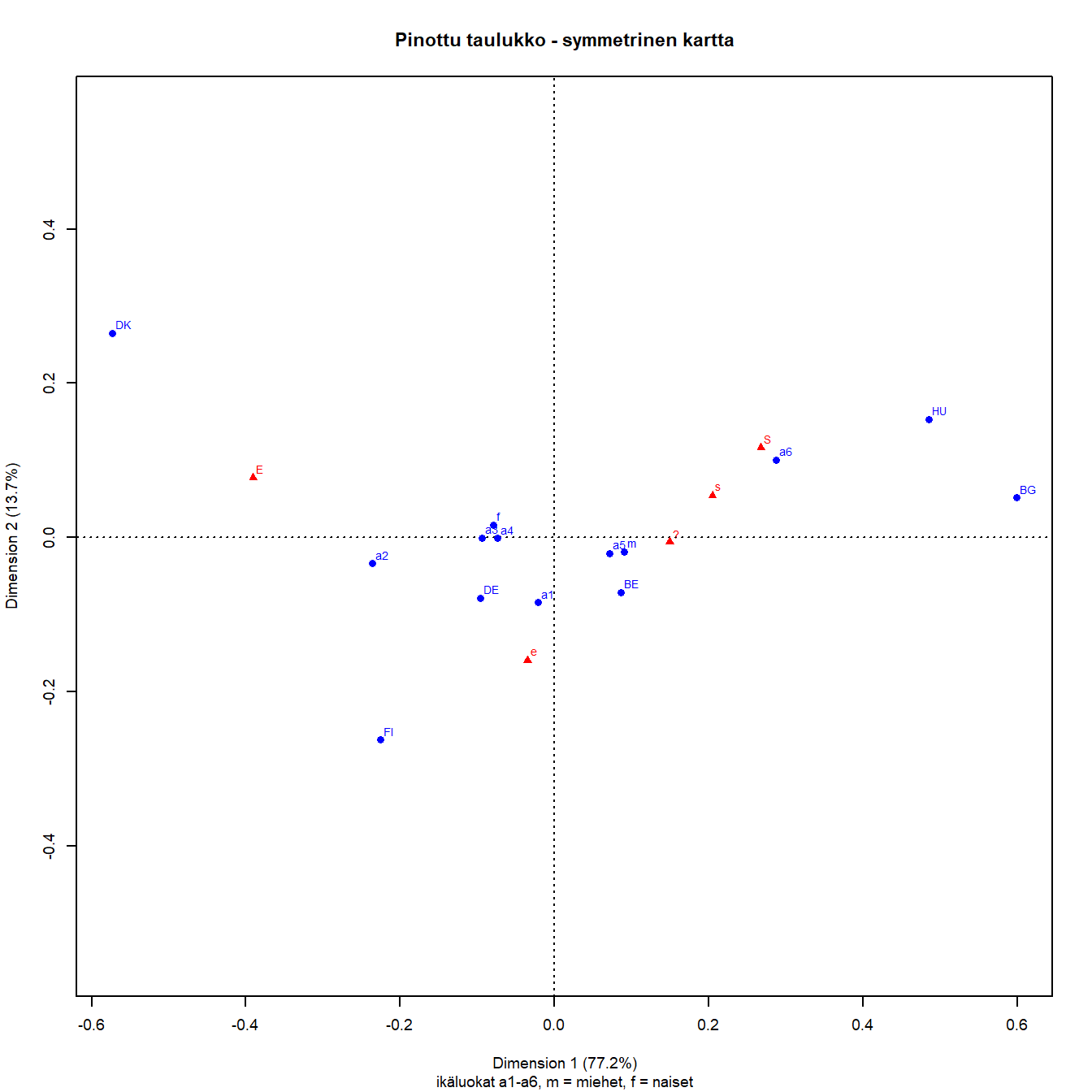
Kuva 7.2: Q1b: Lapsi kärsii jos äiti käy työssä

Kuvassa 7.2 on esitetty pinotun taulukon kartta. Tulkinta ei muutu, eikä maapisteiden sijaintikaan.

Koko aineiston kartassa ikäluokkapisteet ja sukupuolipisteet ovat pakkautuneet maapisteitä tiiviimmin origon ympärille. Ikäluokkapisteiden (koko aineiston keskiarvot) selvä kontrasti on vanhimman (a6) ja toiseksi nuorimman välillä 1. dimension suuntaan.

Ikäluokkapisteet ovat koko aineiston keskiarvopisteitä, niiden sijaintia voi tulkita pistejoukko kerrallaan kuten maapisteidenkin. Naispiste on tiukassa nipussa ikäluokkien a3 ja a4 kanssa aivan origon vasemmalla puolella. Miesten keskiarvopiste on hieman origosta oikealle, yhdessä ikäluokan a5 kanssa.

Lisäpisteet on hyvin esitetty, niiden etäisyyksiä voi luotettavasti arvioida kuvasta. Poikkeus on nuorin ikäluokka (a1, qlt = 501). Inertian osuudet (inr) ovat yhtä vaatimattomia kuin Belgian (28) ja Saksan (29), (m =20, f = 17, a2 = 40, a6 = 83), samoin kontribuutiot akseleiden inertiaan. 1. dimension kontribuutio (ctr) on suuri (>800) kaikilla paitsi nuorimmalla ikäryhmällä (a1) jolla 2. dimension selittää lähes puolet sen inertiasta (470). En esitä numeerisia tuloksia tarkemmin.

Karttaa 7.2 voi verrata karttaan 5.1, jossa on esitetty iän ja sukupuolen yhteisvaikutusmuuttuja. Pinottu taulu on vaihtoehtoinen tapa, ja kartasta 7.2 voi päätellä samat asiat: miehet ovat konservatiivisempia kuin naiset, iäkkäämmät ovat konservatiivisempia kuin nuoret. Nuorin ikäluokka poikkeaa muista.

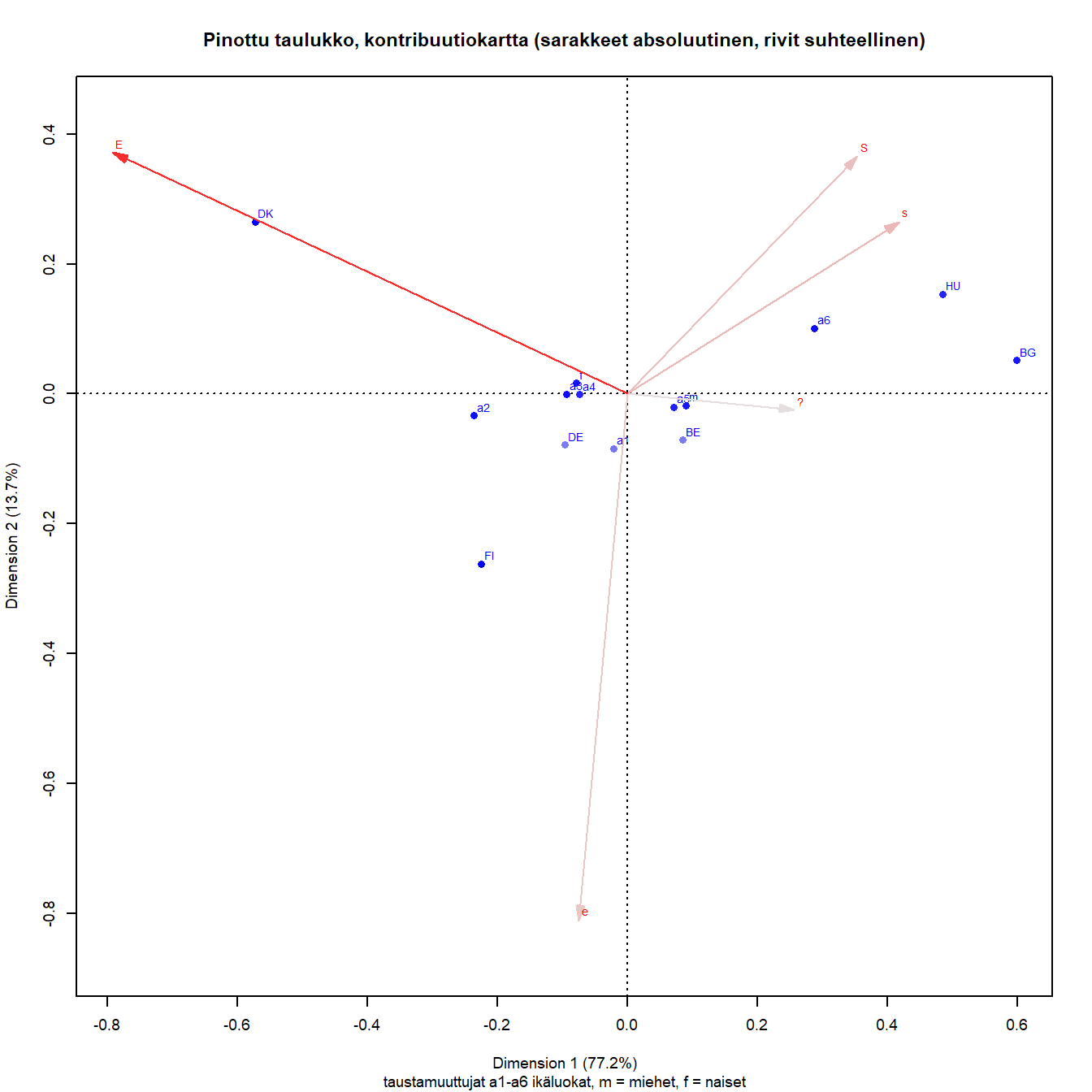
Kuva 7.3: Q1b: Lapsi kärsii jos äiti käy työssä

Kontribuutionkartan (Kuva 7.3) sarakkeista E-sarake (täysin eri mieltä) määrittää akseleita vahvasti, kontrastina kaksi konservatiivista vastausta (S ja s) ja myös neutraali vaihtoehto (e). Numeeriset tulokset kertovat, että ikäluokat vaikuttavat juuri ensimmäiseen tärkeimpään dimensioon.

Belgian ja Saksan pisteet on esitetty kartassa huonosti, samoin nuorin ikäluokka. Muiden pisteiden sijaintia voidaan arvioida myös sarakkeiden ja rivipisteiden välillä. Ikäluokkien kontrasti on selvä toiseksi nuorimman (a2) ja vanhimman (a6) välillä.

Kontribuutiokartalla voi arvioida hieman tarkemmin ikäluokkien ja vastausvaihtoehtojen yhteyttä sarake kerrallaan. Maltillisesti eri mieltä olevien osuus on suhteellisesti suurin nuorimmassa ikäluokassa. Jos a1 - pisteen projisoi konservatiivisen S-vastauksen janalle se ei ikäluokista konservatiivisin. Ikäluokat a2 ja a6 ovat ääripäitä, muut ikäluokat sijoittuvat lähelle toisiaan mutta liberaalille puolelle.

Esimerkkiaineistossa ei ole puuttuvia tietoja. Ne olisivatkin pulmallisia, varianssin dekomponointi ei onnistu, jos reunajakaumat ovat alitaulukoissa selvästi erilaisia.

Matriisien yhdistely on monipuolinen laajennus. Eräs kiinnostava malli on ABBA, kahden rakenteeltaan samanlaisen matriisin yhdistäminen lohkoina. Nimi kertoo yhdistetyn matriisin rakenteen (block circulant matrix), päällekkäin pinotut A ja B liitetään toiseen pinottuun matriisiin B ja A. Matriiseilla on samat rivit ja sarakkeet, esimerkiksi miesten ja naisten vastausprofiilit yhteen kysymykseen maittain luokiteltuina. Kokonaisinertia saadaan dekomponoitua ryhmien sisäiseen ja väliseen hajontaan kahdelle kartalle. Toinen kuvaa maiden välisiä eroja ja toinen maiden sisäisiä sukupuolten välisiä eroja (CAiP ss. 177-).

7.2 Monimuuttujakorrespondenssianalyysi (MCA)

MCA on yhdistettyjen (”pinottujen”) taulukoiden erikoistapaus, samantyyppiset muuttujat taulukoidaan keskenään. Tulos riippuu siis vain muuttujien parittaisista yhteyksistä.

Tätä ”supertaulukkoa” kutsutaan Burtin matriisiksi. Indikaattorimatriisi on toinen tapa esittää data. Indikaattorimatriisin sarakkeet ovat luokittelumuuttujan arvoja (kategorioita) ja rivit yksittäisiä vastausprofiileja. Profiilissa on rivi nollia ja ykkösiä, 1 valitun vaihtoehdon sarakkeessa.

En tässä jaksossa esitä numeerisia tuloksia, mutta niiden tutkimisella voi jatkaa analyysiä.

Tavoite on tutkia seitsemän kysymyksen vastausvaihtoehtojen yhteyksiä, miten ne asettuvat kaksiulotteiselle kartalle. Aikaisemmissa luvuissa etsittiin yhteyksistä uusia piirteitä ja tarkennettiin analyysiä. Nyt hahmotetaan ison aineiston muuttujien välisiä yhteyksiä ja erityisesti puuttuvien tietojen ongelmaa.

Koko datassa (kts. luku 2) on 32823 havaintoa 25 maasta. Niistä täydellisiä on 71 prosenttia. Jos valitaan kuusi taustamuuttujaa (edu, sosta, urbru, maa, ika, sp) ja seitsemän kysymystä, täydellinen havaintoja on 81 prosenttia.

Pelkissä kysymyksissä (Q1a, Q1b, Q1c, Q1d, Q1e, Q2a, Q2b) puuttuvia tietoja on 14 prosentissa havaintoja (4554). Kaikkien puutteellisten havaintojen poistamien (”listwise delete”) on sitä huonompi vaihtoehto mitä enemmän muuttujia on.

Kaikissa kysymyksissä on viisi vastausvaihtoehtoa ja kuudes kategoria puuttuvalle tiedolle.

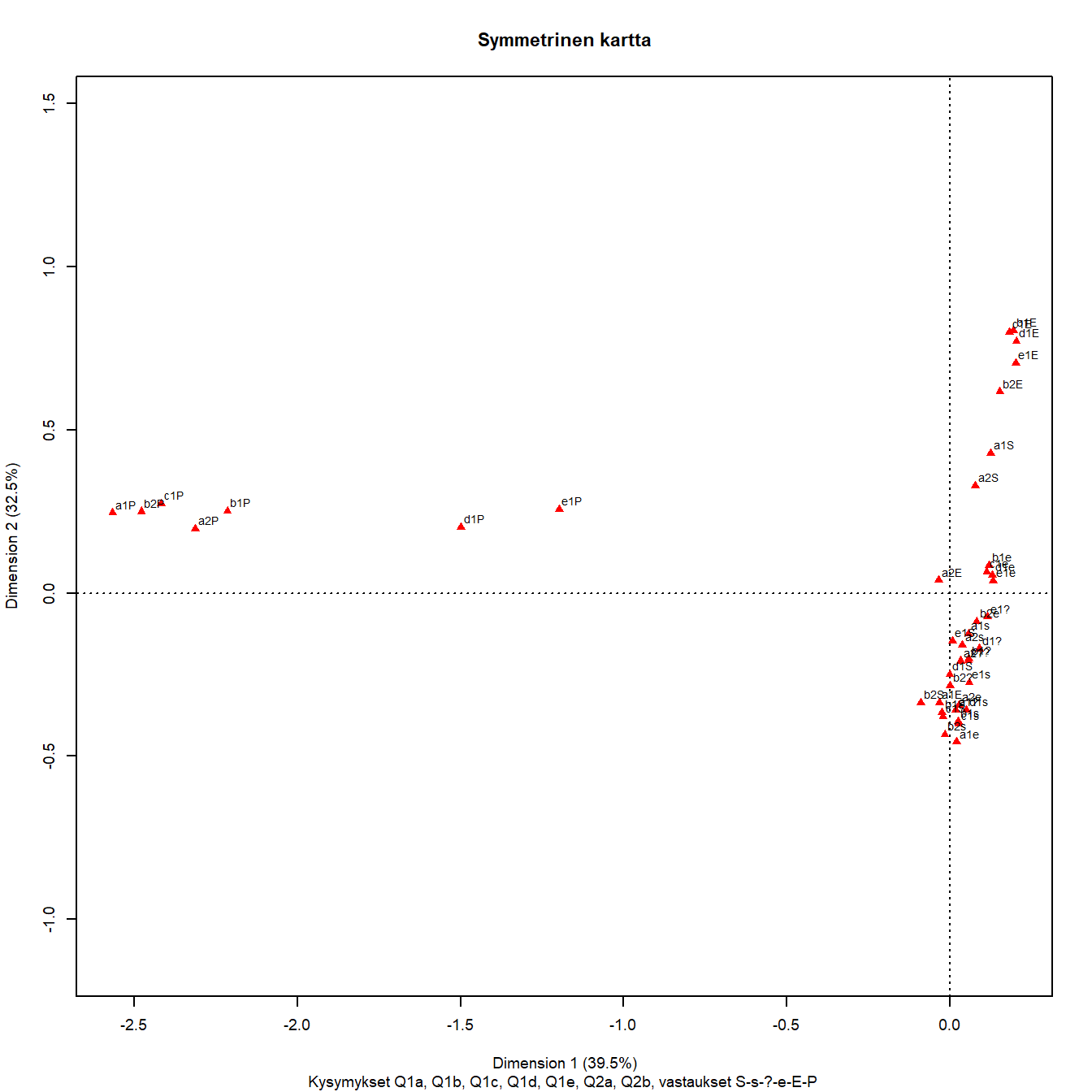
Kuva 7.4: MCA: Seitsemän kysymystä - 25 maata, kartta 1

Kuvasta 7.4 nähdään, että inertian selitysosuudet ovat paljon pienempiä, ja ratkaisu on selvästi kaksiulotteinen. Puuttuvat vastaukset erottuvat omana ryhmänä, ja varsinaiset vastaukset ovat pakkautuneet y-akselin oikealle puolelle. Niiden erot näkyvät vain toisessa dimensiossa. Ensimmäinen dimensio kuvaa vastaamattomuutta, kontrastina kaikki vastauskategoriat. Kokonaisinertiaa on korjattu pienemmäksi (ns. adjusted inetia, kts. liite 1).

Pystyakselin suuntaan kontrasti näyttäisi olevan konservatiiviset ylhäällä, modernit ja liberaalimmat alhaalla. Pisteitä on vaikea erottaa toisistaan.

Karttaa voi parantaa lisäämällä siihen vastaajien pisteet.

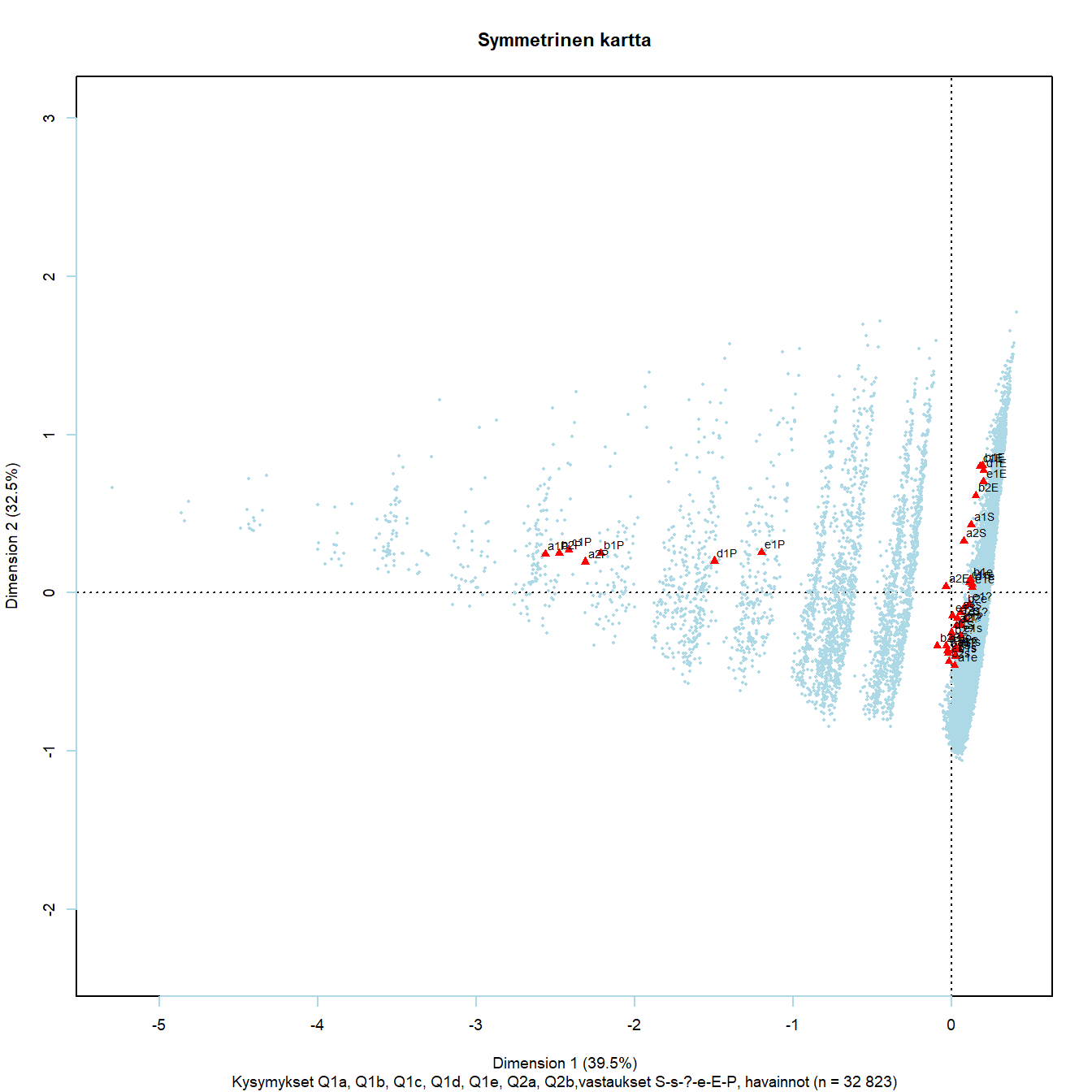
Kuva 7.5: MCA: Seitsemän kysymystä - 25 maata, kartta 2

Kuvassa 7.5 jokainen havainto on sarakevektoreiden keskiarvopiste. Sarakevektoreita ei voi tulkita yhtä selkeästi kuin yksinkertaisessa korrespondenssianalyysissä. Ne eivät edusta kysymystä vaan kysymyksen yhtä vastauskategoriaa.

Pistepilven muoto näyttää, miten pienenevä joukko vastaajia lähestyy kiilana puuttuvien tietojen pisteitä. Kaikkiin kysymyksiin vastanneet ovat massana kuvan oikeassa laidassa. Pistepilvet oikealta vasemmalle kuvaavat kuinka moneen kysymykseen on jätetty vastaamatta.

Osajoukon MCA

Osajoukon MCA sopii hyvin sekä puuttuvien tietojen että täydellisten vastausten analyysiin. Asymmetrisessä kartassa sarakkeet skaalautuvat pois origosta, ja näkyvät paremmin. Kuvaan 7.6 on piirretty havaintopisteet, joista voi hahmottaa havaintojen sijoittumista kartalla.

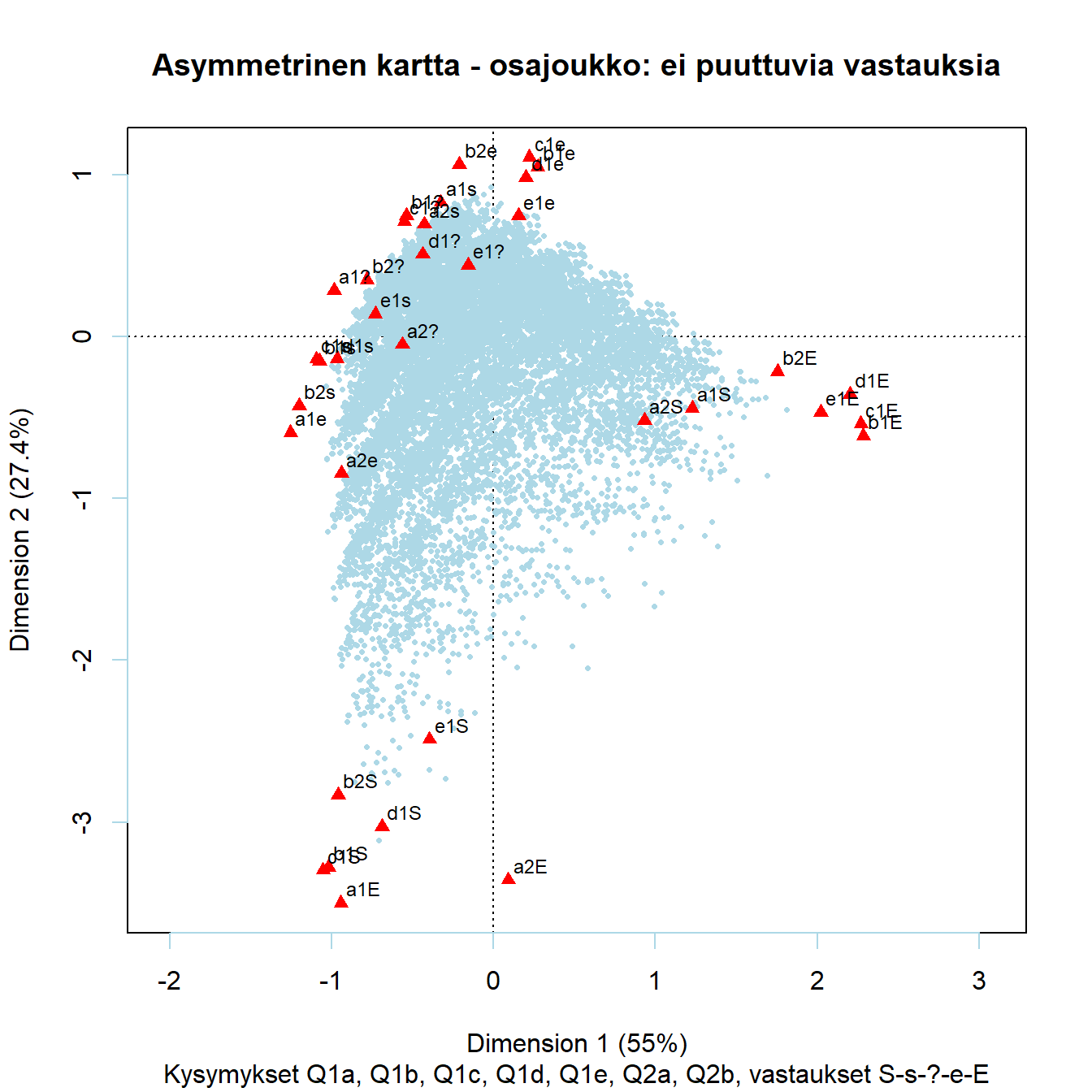
Kuva 7.6: MCA: Seitsemän kysymystä - 25 maata, kartta 3

Kontrasti on “ääripäiden” välillä, vahvat mielipiteet (S ja E) hallitsevat vasenta alakulmaa ja oikeaa laitaa x-akselin tuntumassa. Maltilliset vastaukset ja neutraali vaihtoehto ovat ylhäällä vasemmalla. Liberaalit vastaukset ovat oikealla ylhäällä ja jokaiselle löytää vastinparin vasemmalta alhaalta, konservatiivien kulmasta. Konservatiivisten vastausten joukosta lähimpänä liberaalia ryvästä on “e1S” (“Kotirouvana oleminen on aivan yhtä antoisaa kuin ansiotyön tekeminen” - täysin samaa mieltä). Vastaavasti “a2S” (“Sekä miehen että naisen tulee osallistua perheen toimeentulon hankkimiseen” - täysin samaa mieltä) on lähimpänä konservatiivista kulmaa. Molemmat “ääripäiden maltilliset” pisteet ovat myös omassa ryhmässään lähimpänä maltillisten ja neutraalien vastausten ryhmää.

Karttaan voi hahmotella diagonaalin suuntaisen akselin vahvojen mielipiteiden ryppäiden välille. Muut vastaukset ovat mukaisesti näiden välisellä kaarevalla linjalla (Guttman-efekti).

Greenacre (2010) (s. 139-) analysoi lähes samoja kysymyksiä ISSP-datalla 2002. Tulokset ovat hyvin samantapaisia. Karttaa 7.6 vastaavan kuvan jatkoanalyysi on vasemman yläkulman pisteiden tarkempi analyysi. Greenacre havaitsee, että nämä neutraalit ja maltilliset vastaukset eivät ole hyvin esitettyjä kaksiulotteisella kartalla, vaan ne karkaavat korkeampiin ulottuvuuksiin (“dimensions of middleness”).

Tässä aineistossa kolmiulotteinen MCA antaa samantapaisia viitteitä, mutta vain osa keskikategorioista on huonosti esitetty myös siinä. Huono kvaliteetti on vain osalla sarakkeita (e1? 475, c1? 71 ja b1? 573).