Luku 3 Yksinkertainen korrespondenssianalyysi

Korrespondenssianalyysin peruskäsitteet ja muuttujien yhteyden graafisen analyysin periaatteet voi esittää kahden luokittelumuuttujan ristiintaulukoinnin eli kontingenssitaulun analyysin avulla. Kyse ei ole pelkästään helposta esimerkistä, vaan peruskäsitteet ja geometrisiin perusteisiin nojaava graafinen analyysi ovat oleellisilta osin samat myös monimutkaisemmissa menetelmän sovelluksissa (Greenacre ja Hastie 1987).

Greenacren oppikirjat ovat hyvä esimerkki perusteellisesta yksinkertaisen taulukon analyysin esitystavasta. LeRoux ja Rouanet (2004) korostavat ranskalaisen perinteen mukaisesti matemaattista teoriaperustaa, mutta menetelmän peruskäsitteet ja tulkinnat esitellään yksinkertaisella esimerkillä. Mustonen (1995) käyttää samaa Fisherin Cairness-aineistoa korrespondenssianalyysin esittelyyn.

Esitän tässä luvussa korrespondenssianalyysin peruskäsitteet intuitiivisesti, matemaattiset yksityiskohdat löytyvät liitteestä 1. Kun taulukko on pieni, johtopäätökset voi helposti tarkastaa datasta. Datan analyysin tärkein väline on kuva, yleensä kaksiulotteinen kartta. Tulkinta ja erityisesti väärien johtopäätösten välttäminen vaati kartan tulkinnan varmistamista ratkaisun numeerisista tuloksista. Analysoitava taulukko, sen rivien ja sarakkeiden riippuvuuksia kuvaava kartta ja kartan perustana olevat numeeriset tulokset esitetään yhdessä. Näin tulkinnan perussäännöt on helpompi ymmärtää.

LeRoux ja Rouanet (2004) esittävät tulkinnan perussäännöt hieman eri korostuksella kuin Greenacre (CAiP). Yhteistä on graafisen analyysin tärkeys, mutta ranskalaiset tutkijat korostavat numeeristen tulosten ensisijaisuuta. Analyysi pitää aloittaa tutkimalla numeerisen ratkaisun ominaisuuksia. Greenacren mielestä numeerisia tuloksia tarvitaan johtopäätösten varmistamiseen, ensin katsotaan karttaa. Eroa ei kannata liioitella, molempia tarvitaan. Eksploratiivisessa data-analyysissä näkökulmaa muutetaan, kun datan ominaisuudet tai omituisuudet havaitaan. Kun kartat ovat aina approksimaatiota, numeerisia tuloksia tarvitaan.

3.1 Äiti töissä - kärsiikö lapsi?

Aineistossa on kuuden maan vastaukset kysymykseen Q1b: ”Alle kouluikäinen lapsi todennäköisesti kärsii, jos hänen äitinsä käy työssä”. Kysymys on voimakkaasti muotoiltu. Eräs lastensuojelun ammattilainen piti vastaamista mahdottomana, pitäisi tietää missä lapsi on ja mitä hän tekee. Kysymykset on kuitenkin suunniteltu kokonaisuudeksi, ja niitä analysoidaan yhdessä luvussa 7. Yhden taulukon analyysi esittelee menetelmän, oikeassa tutkimuksessa pitää käyttää vähintään koko kysymyssarjaa.

Tässä tutkielmassa käytetystä aineistosta on poistettu havainnot, joissa tieto vastauksesta puuttuu. Taustamuuttujia ovat vastaajan sukupuoli ja ikä. Taulukoissa vastausvaihtoehtojen tunnuksina käytetään samoja symboleja kuin kuvissa (E = täysin eri mieltä, e = eri mieltä, ? = ei samaa eikä eri mieltä, s = samaa mieltä, S = täysin samaa mieltä).

Frekvenssitaulukossa 3.1 on esitetty vastausten suhteellinen jakauma, lukumäärät on jaettu havaintojen lukumäärällä (8143). Korrespondenssianalyysissä kaikki on suhteellista, ja analyysi perustuu tähän taulukkoon. Taulukon reunajakaumat kertovat jokaisen maan ja jokaisen vastausvaihtoehdon suhteellisen osuuden. Näitä suhteellisia osuuksia kutsustaan korrespondenssianalyysissä rivi- ja sarakemassoiksi.

Taulukko 3.1: Kysymyksen Q1b vastaukset, suhteelliset frekvenssit

	S	s	?	e	E	Total
BE	2.35	5.54	5.38	6.78	4.68	24.72
BG	1.45	4.85	2.52	2.33	0.16	11.31
DE	2.03	4.61	2.43	6.61	5.38	21.05
DK	0.86	2.92	1.87	2.85	8.55	17.05
FI	0.58	2.31	1.83	5.19	3.72	13.63
HU	2.69	3.54	2.76	2.33	0.92	12.24
Total	9.95	23.76	16.79	26.10	23.41	100.00

Muuttujien luonne on usein erilainen. Tähän aineistoon sopii riviprosenttientaulukko, vertaillaan vastausten jakaumia maiden välillä. Taulukon sarakkeet ovat muuttujia ja rivit havaintoja. Rivit on saatu summaamalla (aggregoimalla) vastaukset maittain. Greenacre käyttää näistä yksittäisten vastausten (havaintojen) summariveistä termiä “sample”.

Taulukko 3.2: Kysymyksen Q1b vastaukset, riviprosentit

	S	s	?	e	E	Total
BE	9.49	22.40	21.76	27.42	18.93	100.00
BG	12.81	42.89	22.26	20.63	1.41	100.00
DE	9.63	21.88	11.55	31.39	25.55	100.00
DK	5.04	17.15	10.95	16.71	50.14	100.00
FI	4.23	16.94	13.42	38.11	27.30	100.00
HU	21.97	28.89	22.57	19.06	7.52	100.00
All	9.95	23.76	16.79	26.10	23.41	100.00

Sarakeprosentit antavat toisen näkökulmaan samaan dataan.

Taulukko 3.3: Kysymyksen Q1b vastaukset, sarakeprosentit

	S	s	?	e	E	All
BE	23.58	23.31	32.04	25.98	19.99	24.72
BG	14.57	20.41	15.00	8.94	0.68	11.31
DE	20.37	19.38	14.48	25.32	22.98	21.05
DK	8.64	12.30	11.12	10.92	36.52	17.05
FI	5.80	9.72	10.90	19.91	15.90	13.63
HU	27.04	14.88	16.46	8.94	3.93	12.24
Total	100.00	100.00	100.00	100.00	100.00	100.00

Tavoitteena on korrespondenssianalyysin kartta, jossa rivi- ja sarakepisteet on esitetty samassa kuvassa. Sarakeprosenttien taulukossa on esitetty sarakkeiden suhteelliset jakaumat. Näitä suhteellisia rivejä ja sarakkeita kutsutaan korrespondenssianalyysissä rivi- ja sarakeprofiileiksi.

Korrespondenssianalyysin perusidea on analysoida rivien ja sarakkeiden yhteyttä (korrespondenssia) rivi- tai sarakeprofiilien hajonnan avulla. Hajontaa mitataan poikkeamilla keskiarvorivistä tai sarakkeesta, ja massat otetaan huomioon, kun poikkeamat lasketaan yhteen.

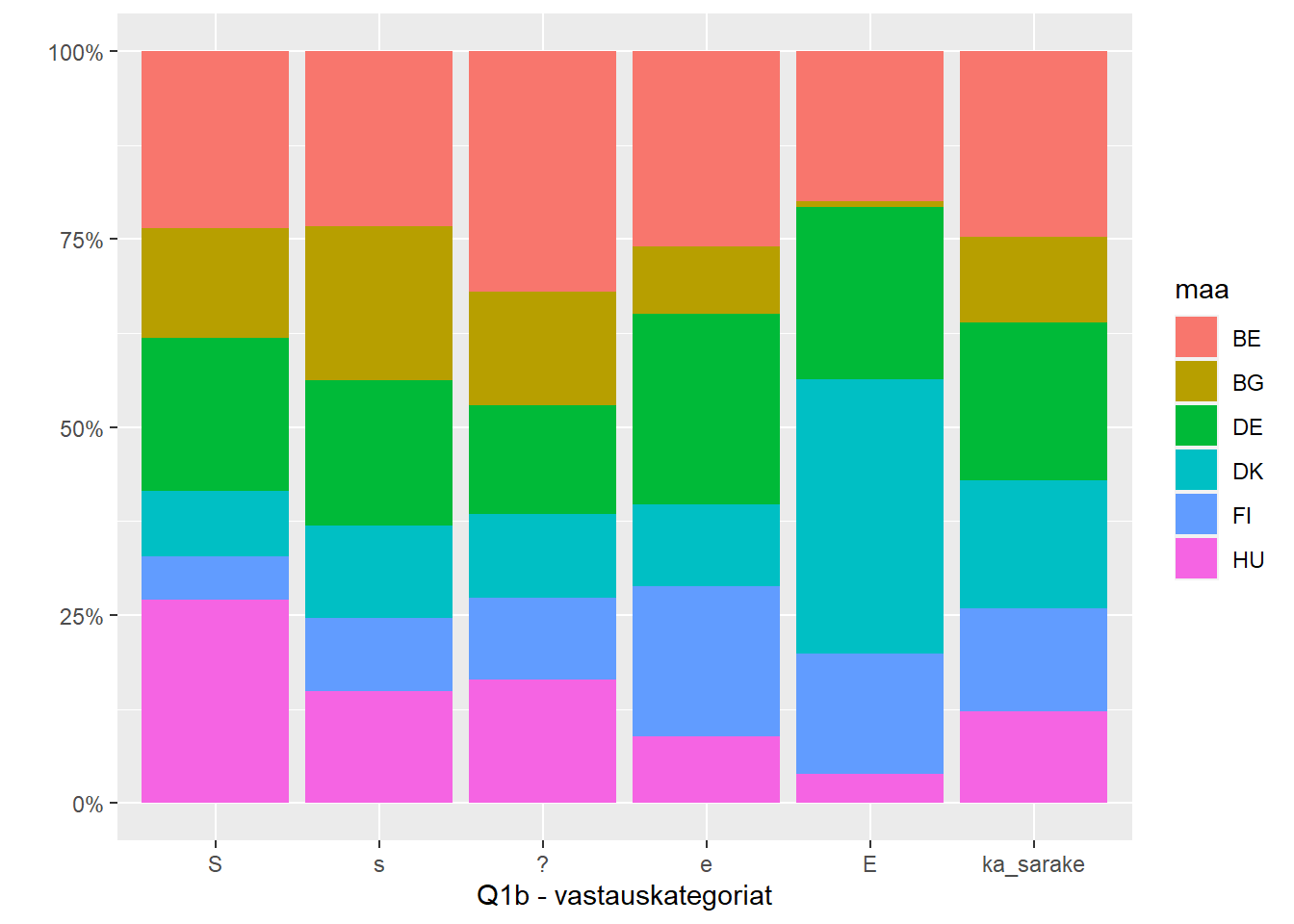
Kuva 3.1: Q1b:Sarakeprofiilit ja keskiarvoprofiili

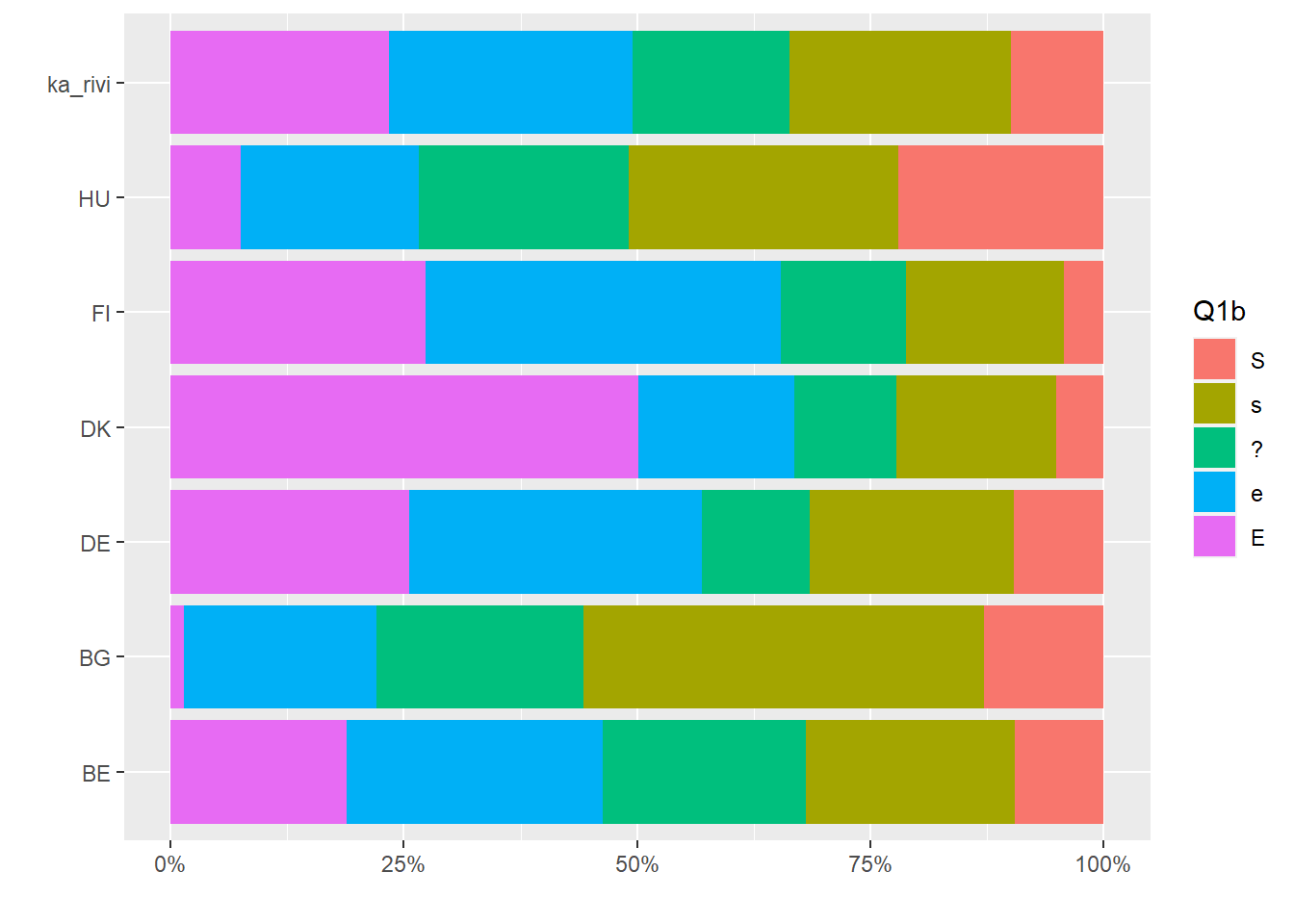
Kuva 3.2: Q1b: riviprofiilit ja keskiarvorivi

Kuvasta 3.2 esimerkiksi näkee, että Tanska (DK) näyttäisi poikkeava keskiarvorivistä paljon, samoin Bulgaria. Bulgarian massa on kuitenkin aineiston pienin (11,31 %), Tanskan taas kohtalainen (17 %). Sarakeprofiilikuvassa 3.1 täysin eri mieltä - vastaus (E) on selvästi erilainen ja sen massa on suuri (23 %). Kaikki luvut ovat suhteellisia, havaintojen lukumäärä ei vaikuta tulkintaan periaatteessa mitenkään.

Mikä on rivien ja sarakkeiden yhteys?

Kahden luokittelumuuttujan riippuvuutta voidaan testata \(\chi^{2}\) - testillä. Riippumattomuushypoteesin mukainen odotettu solufrekvenssi on taulukon 3.1 reunajakaumien alkioiden tulo.

Testisuure saadaan laskemalla yhteen jokaisen solun havaittujen ja odotettujen frekvenssien erotukset muodossa

\[\begin{equation} \chi^{2} = \frac{(havaittu - odotettu)^2} {odotettu}. \tag{3.1} \end{equation}\]

Tämä voidaan esittää korrespondenssianalyysin esittelyyn sopivammalla tavalla parilla muunnoksella, jolloin saamme riveittäin vastaavat termit rivisummalla painotettuna.

\[\begin{equation} rivisumma \times \frac{(havaittu \: riviprofiili - odotettu \: riviprofiili)^2} {odotettu \: riviprofiili}. \tag{3.2} \end{equation}\]

Kun jaamme nämä tekijät havaintojen kokonaismäärällä \(n\), rivisumma muuntuu rivin massaksi, ja niiden summa muotoon \(\frac{\chi^{2}}{n}\).

\[\begin{equation} \frac{\chi^{2}}{n} = \phi^{2}. \tag{3.3} \end{equation}\]

Jakajassa ei ole vapausastekorjausta (n-1), korrespondenssianalyysi on deskriptiivistä data-analyysiä.

Tunnusluku \(\phi^{2}\) on korrespondenssianalyysissä kokonaisinertia (total inertia). Se kuvaa, kuinka paljon varianssia taulukossa on ja inertia on riippumaton havaintojen lukumäärästä. Tilastotieteessä tunnusluvulla on useita vaihtoehtoisia nimiä (esim. mean square contingency coefficient) ja sen neliöjuurta kutsutaan \(\phi\) - kertoimeksi.

Korrespondenssianalyysin ratkaisussa käytetään suhteellisten frekvenssien taulukkoa.

Frekvenssitaulukossa kahden rivin (esimerkiksi rivien 1 ja 3) euklidinen etäisyys on

\[\begin{equation} \sqrt{(p_{11} - p_{31})^2 + (p_{12} - p_{32})^2 + (p_{13} - _{33})^2+ (p_{14} - _{34})^2+ (p_{15} - _{35})^2}. \tag{3.4} \end{equation}\]

Rivien \(\chi^{2}\) - etäisyys on painotettu euklidinen etäisyys, jossa painoina ovat riviprofiilin odotetut arvot. Ne ovat riippumattomuushypoteesin mukaisesti riviprofiilien keskiarvoprofiilin vastaavat alkiot \(r_{i}\) .

\[\begin{equation} \sqrt{\frac{(p_{11} - p_{31})^2} { r_{1}} + \dots + \frac{(p_{15} - p_{35})^2} {r_{5}}} \tag{3.5} \end{equation}\]

Inertia voidaan esittää rivien ja keskiarvorivin (sentroidin) \(\chi^{2}\) -etäisyyksien neliöiden painotettuna summana, jossa painoina ovat rivien massat \(m_{i}\) ja summa lasketaan yli rivien \({i}\).

\[\begin{equation} \phi^{2} = \sum_{i} (massa \: m_{i}) \times (profiilin \: i \: \chi^{2} - etäisyys \: sentroidista)^{2} \tag{3.6} \end{equation}\]

Korrespondenssianalyysin kolme peruskäsitteen “tripletti” – profiili, massa ja \(\chi^{2}\) - etäisyys – on esitelty. “Triplettiä” täydentää “kvartetti”, johon inertia kuuluu.

Rivi- ja sarakeprofiilien taulukoista huomaa, että keskiarvoprofiilien alkiot ovat massoja. Rivien keskiarvoprofiilin alkiot ovat sarakemassoja, ja sama pätee riveille. Tämä rivi- ja sarakeongelmien duaalisuus on yksinkertaisen korrespondenssianalyysin keskeinen idea (CAiP, s. 57). Rivi- tai sarakeongelman ratkaisu tuottaa saman tuloksen.

Ratkaisun dimensio on sarakkeiden tai rivien lukumäärä vähennettynä yhdellä, pienempi kahdesta vaihtoehdosta. Se on myös kokonaisinertian teoreettinen maksimi.

Korrespondenssianalyysi on läheistä sukua pääkomponenttianalyysille. Etäisyysmitta on khii2-etäisyys (käytän tekstissä tätä kirjoitusasua) ja tässä massat ovat mukana painoina. Ratkaisussa etsitään haluttu yleensä kaksiulotteinen ratkaisu (taso), joka minimoi pisteiden khii2-etäisyyksien poikkeamien summan eli on mahdollisimman lähellä pisteitä. Alkuperäisen täyden dimension (full space) data projisoidaan tälle tasolle.

3.2 Symmetrinen kartta

Korrespondenssianalyysi kuvaa taulukon riippuvuudet karttana. Symmetrinen kartta on yleisin ja useiden ohjelmistojen oletuskartta.

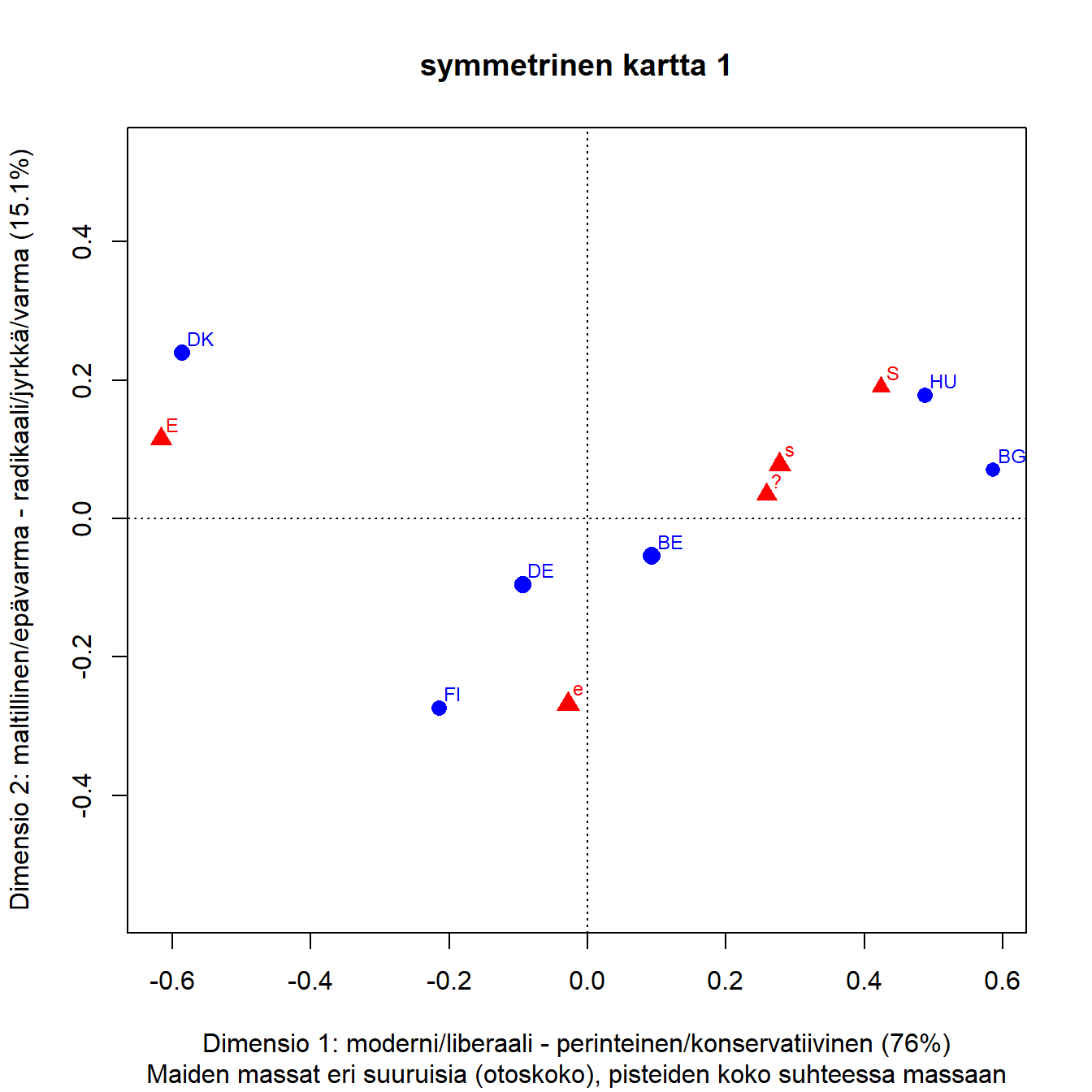
Kuva 3.3: Q1b: lapsi kärsii jos äiti on töissä

Akselien prosenttimerkinnät kertovat, kuinka paljon aineiston inertiasta eli hajonnasta on kaksiulotteisessa projektiossa saatu kuvattua akseleille.

Akselit ovat sisäkkäisiä (nested). Ensimmäinen akseli saa aina suurimman osan inertiasta, tässä 76 prosenttia. Kun toinen akseli kuvaa 15 prosenttia koko inertiasta, on kartalla esitetty 91 prosenttia aineiston hajonnasta. Loput 9 prosenttia jää 3. ja 4. dimensiolle. Nämä ”selitysosuudet” ovat samantapainen laskelma kuin perinteisen regressiomallin ”selitetty” vaihtelu ja ”jäännösvaihtelu”.

Akselien tulkinta on korrespondenssianalyysin perustehtävä. Kontrastit määrittävät akselien tulkinnan. Benzacrin ohjeen mukaan ( LeRoux ja Rouanet (2004), s.49) katsotaan mitä on oikealla ja mitä vasemmalla. Akselien tulkinta perustuu siihen, mitä yhteistä on kaikilla elementeillä, jotka ovat origon vasemmalla puolella ja vastaavasti origon oikealla puolella. Samalla tavalla tulkitaan toinen akseli, mitä on ylhäällä ja alhaalla. Tulkinta tehdään akseleiden suuntaan. Kuvan tulkintaa ei aloiteta pisteiden etäisyyksiä vertailemalla.

Kun taulukon rivit ovat havaintoja ja sarakkeet muuttujia, akselien tulkinta tehdään muuttujien avulla. Vasemmalla on E ja oikealla puolella samanmieliset vastaukset s ja S. Neutraali ”?” on s-vastausten vasemmalla puolella mutta kuitenkin oikealla. Kuvan perusteella ei voi sanoa kuinka paljon, kaikki erot ovat suhteellisia.

Sarakkeet ovat oikeassa järjestyksessä, mutta niiden koordinaatit x-akselilla eivät olen tasavälisiä. Jos muuttuja jostain syystä halutaan esittää välimatka- tai suhdeasteikon muuttujana koordinaatti ensimmäisellä dimensiolla on yksi vaihtoehto.

Ensimmäisen dimension tulkinta on aika selkeä. Toinen akseli on kontrasti lievemmän tai maltillisemman erimielisyyden (e) ja muiden vastausten kanssa. Se on 1. dimension suuntaan kaikkein lähimpänä origoa. Hieman varovaisemmin akselin voi tulkita maltillisen ja jyrkemmän tai varmemman mielipiteen kontrastiksi.

En jatkossa esitä kuvailevia akseleiden nimiä kuvissa, akseleiden tulkinta olisi kumminkin analyysin ensimmäinen tehtävä.

Maiden vertailu tehdään näiden akselien suuntaan. Sekä sarakepisteiden että rivipisteiden keskinäiset välimatkat approksimoivat optimaalisesti niiden khii2-etäisyyksiä. Sarake- ja rivipisteiden välisillä etäisyyksillä ei ole mitään suoraa tulkintaa. Pisteiden etäisyydet samassa pistepilvessä ovat suhteellisia, Saksa on konservatiivisempi kuin Suomi mutta emme tiedä kuinka paljon. Maiden järjestys oikealta vasemmalle on selkeä, Tanska on vasemmalla liberaalina ”ääripäänä”, oikealla taas Unkari ja Bulgaria. Pystyakselin suuntaan nähdään, että kaikkein ”maltillisin” mutta kuitenkin liberaali on Suomi, jyrkimmät mielipiteet löytyvät Unkarista ja Tanskasta.

Näitä tulkintoja voi vertailla edellä esitettyihin kahteen kuvaan rivi- ja sarakeprofiileista. Näkeekö niistä helposti saman riippuvuuden rakenteen? Kartta kertoo selvästi enemmän, mutta vaati ensin tulkinnan.

Kartta on approksimaatio neliulotteisen pistepilven hajonnalle. Vain origo on siinä tarkasti esitetty. Se on koko aineiston keskiarvopiste, ja pisteiden hajonta sen ympärillä kuvaa poikkeamaa riippumattomuushypoteesista.

Tärkeä geometrinen periaate on se, että kaukana on kaukana myös alkuperäisessä pistepilvessä, mutta kartalla lähellä olevat pisteet eivät välttämättä ole lähellä. Projektio kutistaa pisteiden etäisyyksiä.

Approksimaation laatu selviää korrespondenssianalyysin numeerisista tuloksista, samoin se miten rivi- ja sarakepisteen määrittävät akselit.

Kartoissa tärkein tekninen yksityiskohta on kuva- tai muotosuhde (aspect ratio). Akseleiden mittayksikön pitää olla sama eli muotosuhteen yksi. Jos kuvia tulostetaan useassa formaatissa kannattaa olla tarkkana. Kuvien on jo analyysivaiheessa oltava lukukelpoisia, ja symbolien kokoa joutuu isoissa aineistoissa säätämään. Tulosten esittäminen lopullisessa muodossa vaatii jo paljon vaivannäköä, tässä tutkielmassa esitetään vain datan analysoinnin valikoituja kuvia. Tutkielman karttojen ulkoasu ei ole paras mahdollinen, mutta tarkoitukseen riittävän hyvä. Graafinen data-analyysi on vaivatonta vasta sitten kun se tehty.

Vaatimukset datalle

Korrespondenssianalyysin sovelletaan yleisimmin frekvenssitaulujen analyysiin, lukumäärädataan (count data). Periaatteessa mikä tahansa data sopii, kunhan se voidaan järkevästi esittää suhteellisina lukumäärinä (relative amounts), siis suhdeasteikon (ratio scale) muuttujana. Tässä oleellista on tulkittavuus tutkimusongelman näkökulmasta. Välttämätön ehto on sama mittayksikkö: lukumäärä, rahayksikkö, pituusmitta kelpaavat (CAiP s. 15). Taulukon lukujen on oltava ei-negatiivisia (positiivisia, nolla sallittu).

Rajat ovat joustavia, kun mukaan otetaan erilaiset uudelleenskaalaukset ja transformaatiot. Tämä oli menetelmän perusidea jo Benzecrillä (CAiP, s. 201).

Menetelmää sovelletaan profiileihin, jotka painotetaan massoilla, ja profiilien etäisyyksiä mitataan khii2-etäisyysmitalla. Jos datan voi esittää tässä muodossa, menetelmää voi käyttää.

3.3 Asymmetrinen kartta ja ideaalipisteet

Symmetrisessä kartassa (Kuva 3.3) molemmat pisteparvet on esitetty pääkoordinaateissa (principal coordinates) ikään kuin päällekkäin, samassa kuvassa.

Toinen vaihtoehto on asymmetrinen kartta, jossa toinen pistejoukko esitetään standardikoordinaateissa ja toinen pääkoordinaateissa. Asymmetrisessä kartassa (Kuva 3.4) sarakkeet on esitetty standardikoordinaateissa ja rivit pääkoordinaateissa.

Sarakepisteitä kutsutaan ideaalipisteiksi, ne edustavat kuvitteellisia maita, joissa kaikki vastaukset ovat samoja. Matemaattisesti kartalle projisoidut ideaalipisteet ovat (tässä esimerkissä) neliulotteisen avaruuden verteksin (monikulmion) kärkipisteitä. Rivipisteet ovat tämän verteksin sisällä.

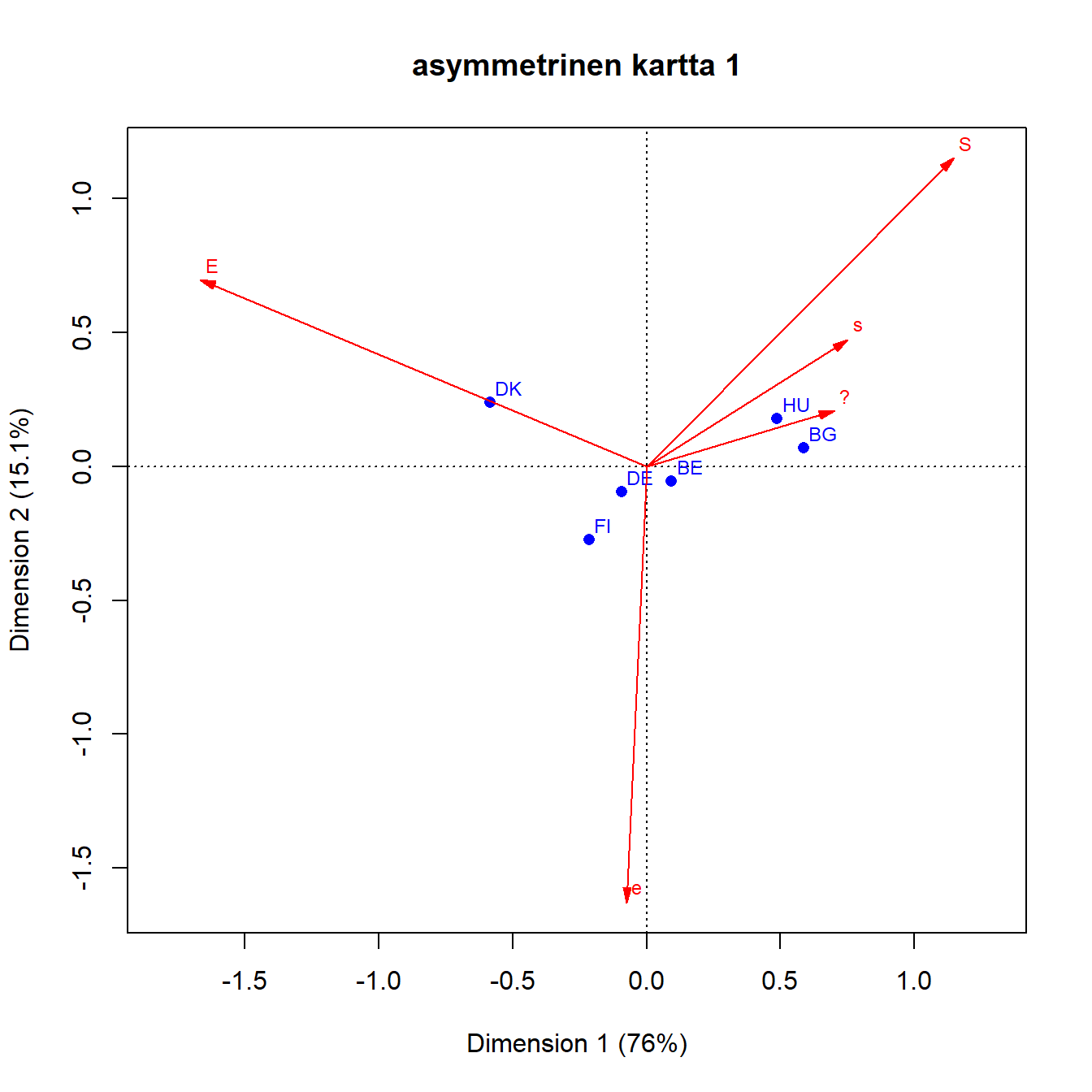
Kuva 3.4: Q1b: lapsi kärsii jos äiti on töissä

Sarakepisteet kuvaavat maksimi-inertiaa, ja rivipisteiden paljon pienempi hajonta kuvaa niiden poikkeamaa tästä hypoteettisesta tilanteesta. Sarakepisteet skaalautuvat origosta ulospäin. Asymmetrisessä kartassa rivi- ja sarakepisteiden etäisyydellä on tulkinta, samoin rivipisteiden välisellä etäisyydellä. Sarakepisteiden välisillä etäisyyksillä ei ole tulkintaa. Sarakepisteet on skaalattu ja mittakaavan ero symmetriseen karttaan näkyy selvästi.

Ideaalipisteiden tulkinnan voi varmistaa sarake kerrallaan, projisoimalla rivipisteet origon kautta piirretylle janalle. Kuvassa 3.5 nähdään mikä on maiden järjestys E-vastausvaihtoehdossa.

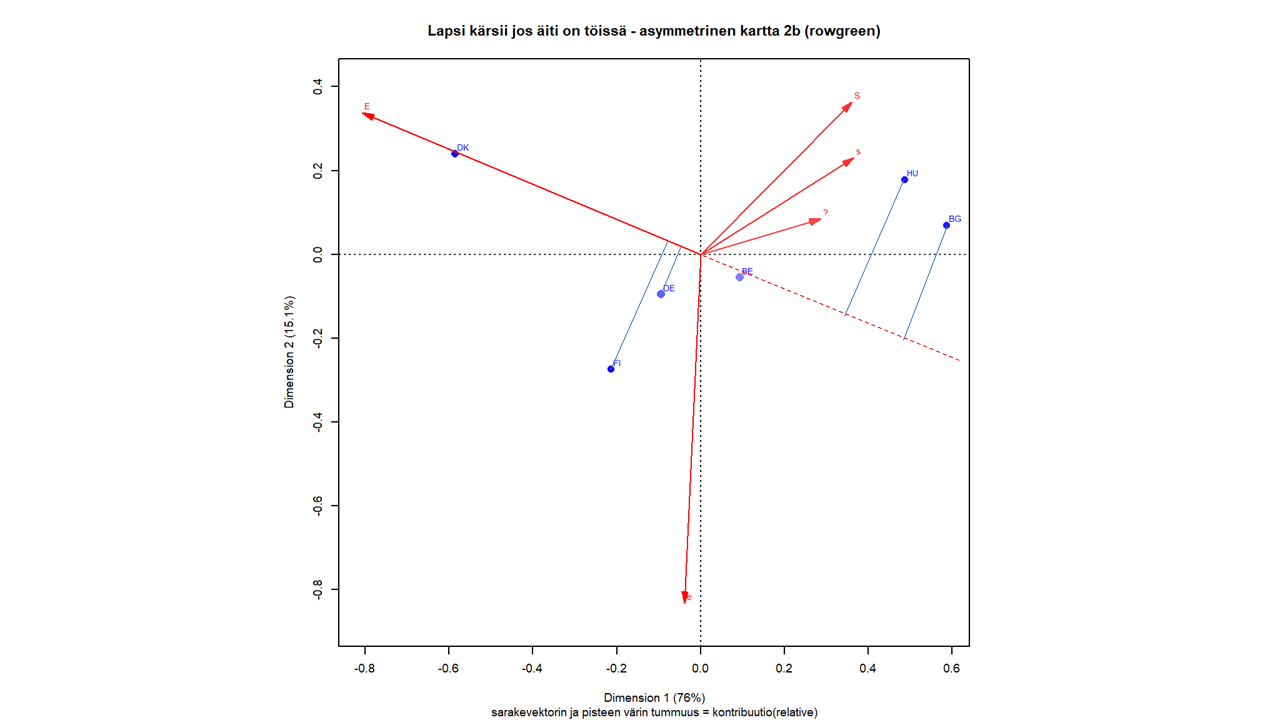
Kuva 3.5: Rivipisteiden projektiot

Asymmetrinen kartta antaa toisen näkökulman rivien ja sarakkeiden suhteeseen. Sen huono puoli on ideaalipisteiden karkaaminen kauas origosta ja rivipisteiden pakkautuminen pieneksi parveksi. Jos rivipisteiden hajonta on suuri, kuva on käytännöllinen. Kyselytutkimusaineistoissa näin ei yleensä ole.

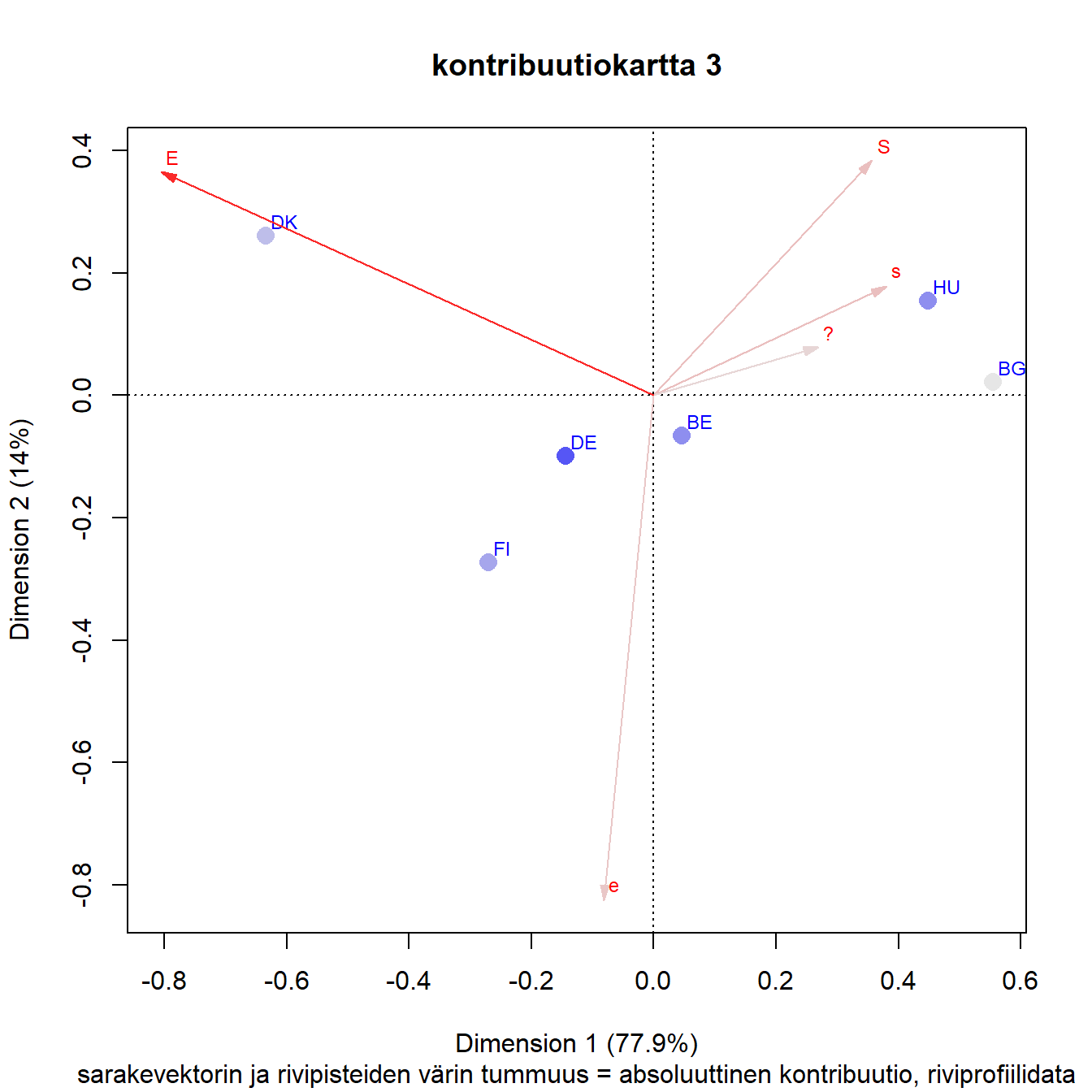
3.4 Kontribuutiot kartalla

Kartassa (Kuva 3.3) on esitetty myös pisteiden massat. Tässä aineistossa pisteiden tai sarakesymbolien kokoerot eivät kovin selvästi erotu, mutta yleiskuvan ne kertovat.

Rivipisteiden ja sarakkeiden kontribuutiot voidaan esittää kartalla värisävyinä.

Kun kartalla pistejoukon inertia kuvataan akseleille, on jokaisella pisteellä oma osuutensa akseleiden kuvaamasta inertiasta. Absoluuttinen kontribuutio kertoo rivin tai sarakkeen osuuden akselin inertiasta. Vaikutuksessa on mukana pisteen massa.

Suhteellinen kontribuutio kertoo akselin osuuden pisteen inertiasta. Tämä tunnusluku kuvaa pisteen projektion laatua, kuinka hyvin se on kartalla esitetty.

Kontribuutiokartta on asymmetrinen kartta, jossa sarakevektorit on skaalattu kertomalla ne massojen neliöjuurilla. Näin sarakevektorit “kutistuvat” kohti origoa mutta vektorin pituus kertoo edelleen sen suhteellisen massan. Kartta sopii niin pienen kuin suuren inertian tilanteisiin (M. Greenacre 2006).

Absoluuttiset kontribuutiot

Absoluuttisten kontribuutioiden jakautumista akseleille voi varovaisesti päätellä sarakevektorin ja akseleiden välisistä kulmista. Mitä lähempänä sarakevektori on akselia, sitä suurempi on sen osuus akselin inertiasta. Samanlaisia päätelmiä voi tehdä myös rivipisteistä hahmottamalla niistä janan origoon.

Käsitteisiin palataan tarkemmin seuraavissa luvuissa ja teorialiitteessä, ja liian tarkkaan karttaa ei kannata tutkia. Numeeriset tulokset ovat yksityiskohdissa selkeämpiä.

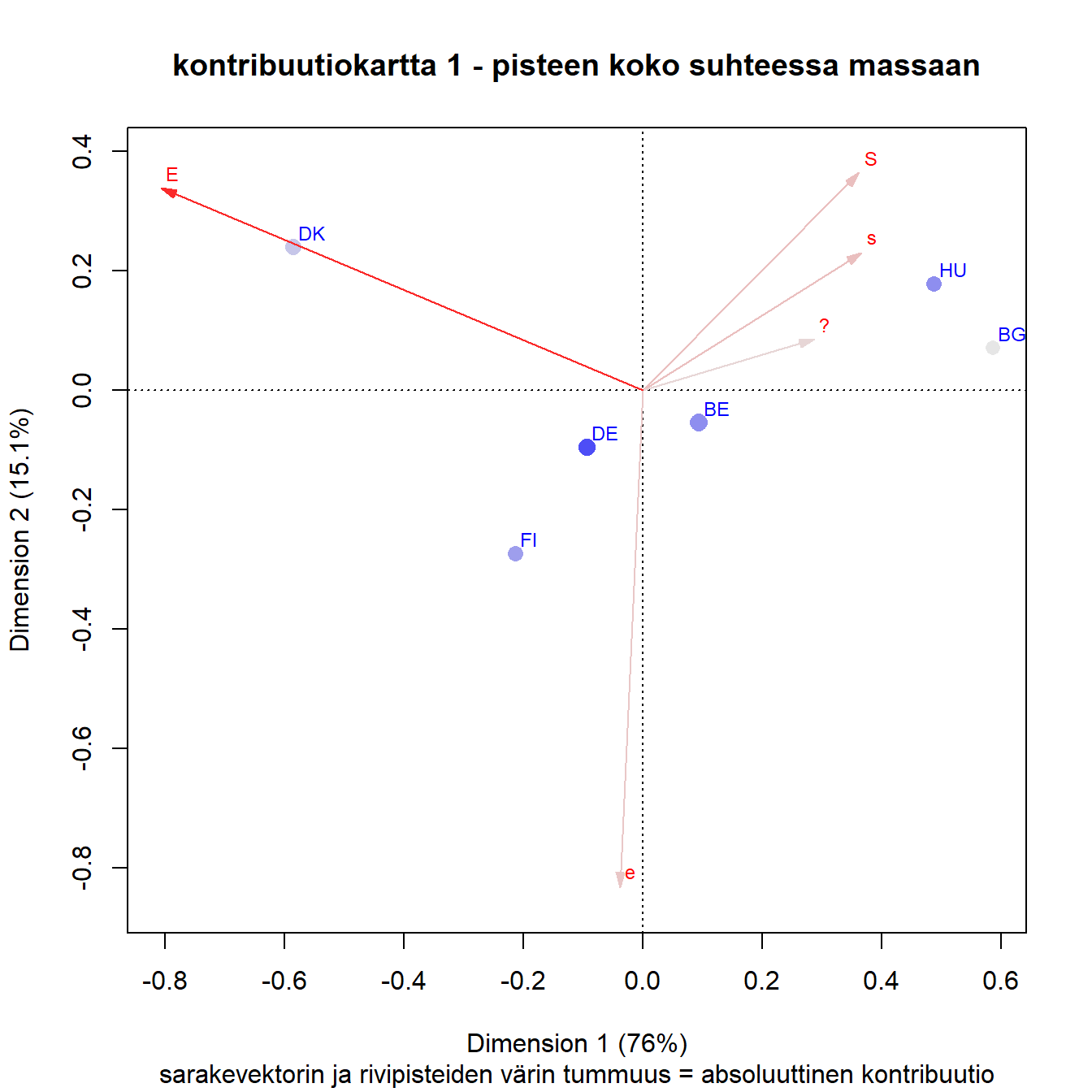
Kuva 3.6: Q1b: lapsi kärsii jos äiti on töissä

Sarakkeista ratkaisuun vaikuttaa selvästi eniten E, ja juuri ensimmäiseen dimensioon, joka selittää suurimman osan kokonaisinertiasta. Toista dimensiota määrittää vahvimmin e, mutta myös kaikki muut sarakkeet x-akselin yläpuolella. Samaa mieltä olevien (S ja s) vaikutus näyttäisi jakautuvan selvimmin molemmille dimensioille.

Vaikka massojen suhteellisia eroja ei kovin helposti pistekoosta erota, se näkyy epäsuorasti Saksan melko vahvana kontribuutiona. Bulgarian pieni kontribuutio näyttäisi olevan ensimmäiselle dimensiolle. Belgian kontribuutio ratkaisuun on pienempi kuin Saksan vaikka sen massa on hieman suurempi. Belgian ja Saksan pisteet ovat suhteellisesti lähempänä origoa jo suuren massansa ansiosta.

Suhteelliset kontribuutiot

Sarakkeiden laatu näyttäisi olevan hyvä, mutta rivipisteistä Saksa ja erityisesti Belgia erottuvat hieman heikommin esitettyinä.

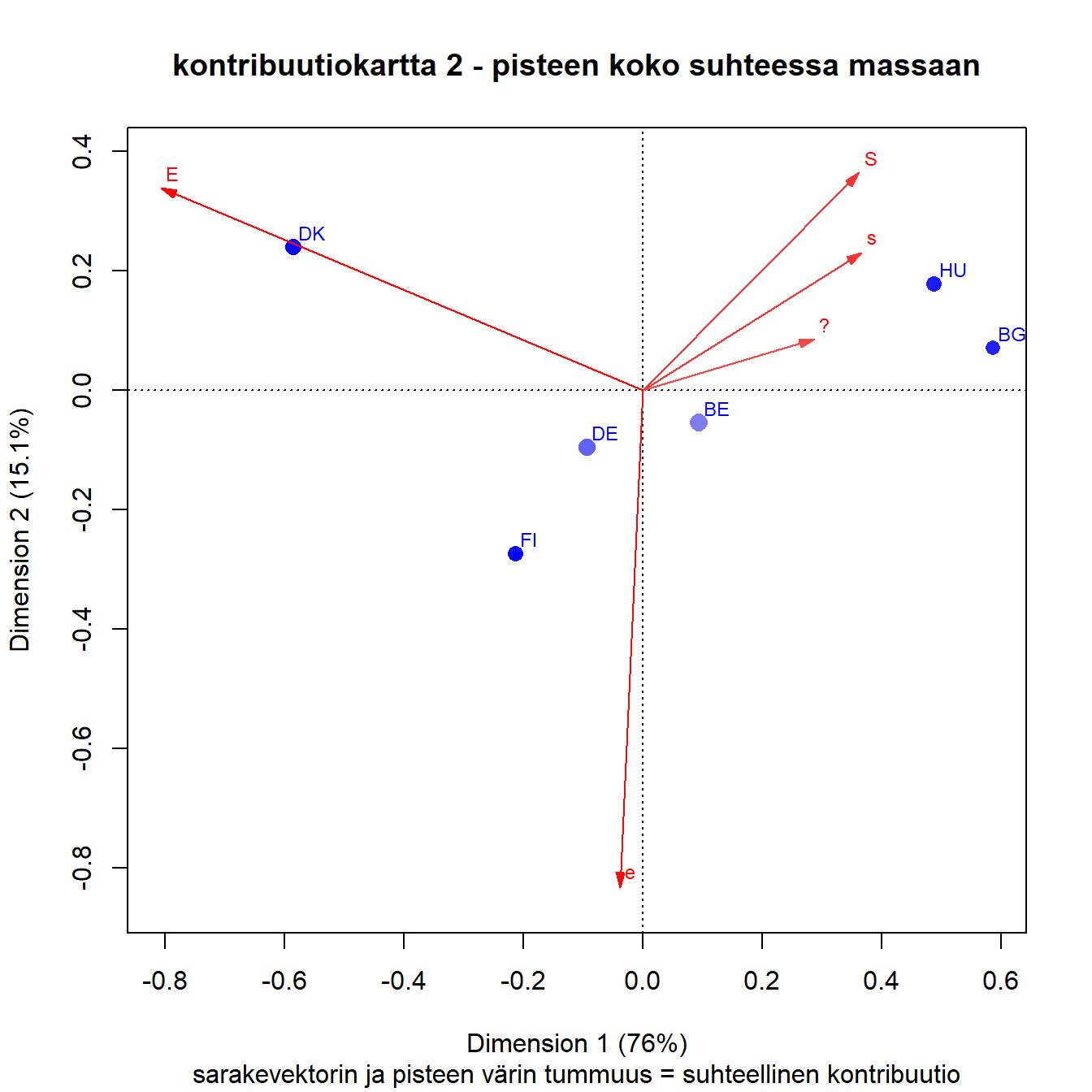
Kuva 3.7: Q1b: lapsi kärsii jos äiti on töissä

Massojen ja kontribuutioiden esittäminen kartoilla näyttää selkeimmin poikkeavat pisteet. Kontribuutioiden graafinen tarkastelu antaa myös yleiskuvan, jonka voi varmistaa numeerisista tuloksista.

Kaikki edellä esitetyt päättelyt perustuvat tietysti kaksiulotteiseen projektioon. Jos pisteet on esitetty hyvin eli niiden inertiasta (poikkeamasta keskiarvosta) suuri osa on kuvattu kartalle, rivipiste on sitä lähempänä ideaalipistettä mitä suurempi ideaalipisteen osuus on sen profiilissa.

3.5 Massat

Massat ovat korrespondenssianalyysin keskeinen käsite, ja niiden kaksoisrooli on menetelmässä tärkeä. Massat ovat normalisoiva muunnos khii2-etäisyysmitalle ja profiilien painoja.

Tässä jälkimmäisessä roolissa massat liittyvät tutkimusongelmaan, mitä halutaan vertailla? Kun vertaillaan eri maita, ei ole kovin perusteltua käyttää massoina eri maiden otoskokoja. Jos taas halutaan vertailla vaikkapa miesten ja naisten vastauksia on luonnollista normalisoida miesten ja naisten massat yhtä suuriksi. Rivi- ja sarakemassat ovat verrannollisia taulukon rivi- ja sarakesummiin, frekvenssitaulukon reunajakaumiin. Ne voidaan tutkimusongelmaan sopivalla tavalla skaalata uudelleen. Kun esimerkiksi vertaillaan viittä koulutustaso-ryhmää massat skaalataan verrannollisiksi niiden väestötason osuuksiin (CAiP, s. 23). Tällainen datan esikäsittely on normaali osa korrespondenssianalyysin soveltamista.

Jos massat halutaan vakioida osajoukoissa yhtä suuriksi, ratkaisu on yksinkertainen. Korrespondenssianalyysin taulukoksi otetaan riviprofiilitaulukko, jossa rivien summat ovat yksi.

Kuvassa 3.8 on tehty näin, ja kartta eroaa hämmästyttävän vähän maiden otoskokoja massoina käyttävästä kartasta 3.3.

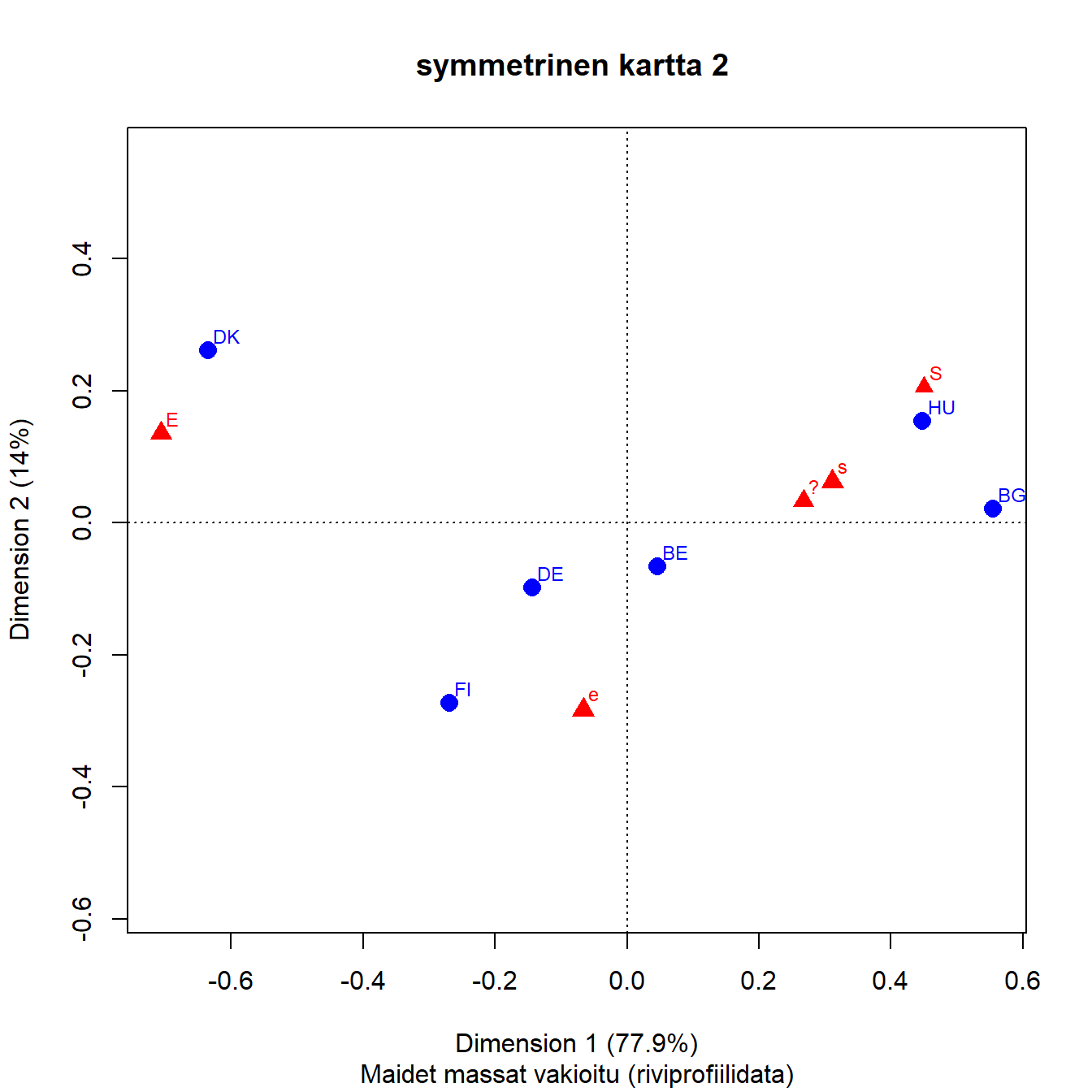
Kuva 3.8: Q1b: lapsi kärsii jos äiti on töissä

Pienimpien otosten maat (Bulgaria, Unkari) liikahtavat hieman origoa kohti, Bulgaria hieman enemmän kohti maltillista puolta y-akselin suuntaan.

Kuva 3.9: Q1b: lapsi kärsii jos äiti on töissä

Kontribuutiokartta 3.9 ei juuri eroa edellä esitetystä kartasta 3.6.

En ole vakioinut vertailtavien ryhmien (tässä maat) suhteellisia osuuksia. Syy on yksinkertainen: esittelen menetelmää sen perusmuodossa ilman kovin täsmällisiä tutkimusongelmia. Oikeiden tutkimuskysymysten vastauksia pitää tietysti etsiä järkevillä massojen skaalauksella. Korrespondenssianalyysi on inertian dekomponointia, jakamista osiin.

3.6 Karttojen erot

Yksinkertaisen korrespondenssianalyysin peruskuva on symmetrinen kartta. Ehkä yllättäen sen “…tulkinta on edelleen menetelmän kaikkein kiistanalaisin aspekti” (CAiP s.295, M. Greenacre (2006)).

Sarake- ja rivipisteet esitetään siinä ikään kuin päällekkäin, samassa koordinaatistossa. Niiden pääkoordinaatit ovat kuitenkin eri pistejoukoista tai avaruuksista. Asymmetrisessä kartassa pisteet ovat samassa avaruudessa, ja ero on Greenacren mukaan vain skaalaus. Asymmetrisessä kartassa standardikoordinaateissa esitetyt ideaalipisteet skaalataan pääakselien suunnassa vastaavilla pääakselien inertioiden neliöjuurilla.

Kun akselien inertioiden (principal inertias) neliöjuuret eivät ole liian erisuuruisia, ideaalipisteiden suuntavektorit ovat lähes saman suuntaisia pääkoordinaateissa ja standardikoordinaateissa.

Jos pääinertioiden neliöjuuret ovat hyvin eri suuruisia, tulkintaongelmia voi tulla, mutta niillä ei käytännössä ole merkitystä. Siksi Greenacre pitää skaalausdebattia akateemisena kiistana, käytännön sovelluksissa sillä ei ole merkitystä. Greenacre (1989) kommentoi skaalausta perusteellisesti, kiista on ollut aika sitkeä mutta lienee laantunut.

Symmetrinen kartta on hyvä vaihtoehto, sillä asymmetrisessä kartassa skaalaus vie ideaalipisteet usein kauas ja pääkoordinaateissa esitetyt pisteet pakkautuvat kuvan keskelle. Jos dataa tulkitaan asymmetrisesti kontribuutiokartta on hyvä vaihtoehto. Silloin rivipisteiden khii2-etäisyydet esitetään optimaalisesti ja sarakkeiden suuntavektoreille projisoiduilla pistellä on kaksoiskuvatulkinta.

Greenacren mukaan kartoilla voi tavoitella kolmea eri asiaa. Kuvassa voi esittää rivipisteiden etäisyydet, sarakepisteiden etäisyydet tai rivi- ja sarakepisteiden etäisyydet. Jälkimmäinen on kaksoiskuvien (biplot) ns. skalaaritulo-ominaisuus. Rivi- ja sarakepisteen skalaaritulo “palauttaa” alkuperäisen datan, tässä tapauksessa taulukon solun.

Edellä mainituista tavoitteista vain kaksi voidaan optimaalisesti esittää yhtä aikaa.

Symmetrisessä kartassa khii2-etäisyydet rivipisteiden välillä ja sarakepisteiden välillä esitetään optimaalisesti. Rivi- ja sarakepisteiden välisiä etäisyyksiä ei esitetä optimaalisesti, mutta ne voidaan tulkita kohtalaisen hyvin, jos pääakselien inertioiden neliöjuuret eivät ole liian erisuuruisia.

Asymmetrisessä kartassa pääkoordinaateissa esitetyn pistejoukon etäisyydet kuvataan optimaalisesti, standardikoordinaateissa esitetyt pisteet ovat “ääriprofiileja”, verteksin kulmapisteitä. Rivi- ja sarakepisteiden etäisyydet esitetään optimaalisesti, mutta sarakepisteiden etäisyyksillä ei ole suoraa tulkintaa,

Kontribuutiokartta on muunnelma asymmetrisestä kartasta. “Ääriprofiilit” vedetään kohti origoa kertomalla ne massojen neliöjuurilla. Näin kuva selkenee, ja “kutistetun” pisteen etäisyys origosta kertoo sen kontribuution pääakseleille. Näiden pisteiden välisillä etäisyyksillä ei ole suoraa tulkintaa.

Jako standardi- ja pääkoordinaatteihin on suora seuraus korrespondenssianalyysin matemaattisesta ratkaisusta. Greenacre esittelee kaksoiskuvia käsittelevässä kirjassaan (Greenacre 2010) selkeästi koordinaattien yhteyden ratkaisualgoritmiin, singulaariarvohajotelmaan.

Koordinaattien yhteys voidaan esittää kahtena yksinkertaistettuna kaavana (M. Greenacre ja Primicerio (2013), s.174):

\[\begin{equation} pääkoordinaatit = standardikoordinaatit \times \sqrt{pääakselien \: inertiat} \tag{3.7} \end{equation}\]

\[\begin{equation} kontribuutiokoordinaatit = \sqrt{massat} \times standardikoordinaatit \tag{3.8} \end{equation}\]